На рисунке, а представлен бипланетарный механизм, состоящий из трех планетарных контуров [1]. Обозначим эти контуры А, В, С соответственно. Планетарный механизм А образуется из звеньев 1, 4 и 6; В ― из звеньев 1, 2 и 5;С―из звеньев 2, 3, и 4, в котором водило-сателлит 2 является сателлитом первой ступени, 3―сателлитом второй.
Кинематические схемы бипланетарных механизмов, аналогичных указанному на рисунке, а, будем считать полными. Наряду с полными существуют частные кинематические схемы. Например, при отсутствии планетарного контура А (за счет ликвидации звена 4) или В (за счет ликвидации звеньев 5 и 2) механизм также будет бипланетарным. 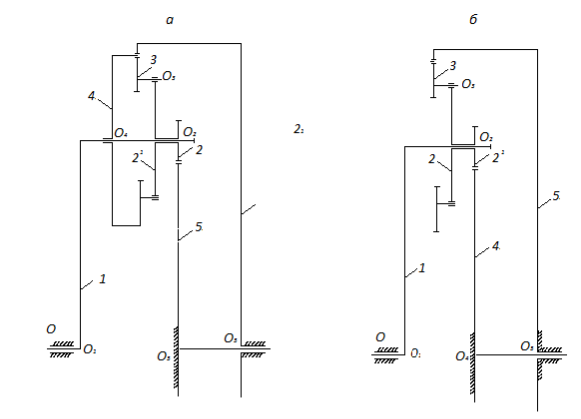
Каждый из приведенных планетарных контуров может иметь три варианта сцепления сателлита с центральным колесом [2]:
![]()
![]()
![]()
Комплекс вариантов позволяет создать следующие неповторяющиеся варианты кинематических схем полного бипланетарного механизма (рисунок, а):
|
A1 B1 C1 |
A2 B1 C1 |
A3 B1 C1 |
|
A1 B2 C1 |
A2 B2 C1 |
A3 B2 C1 |
|
A1 B3 C1 |
A2 B3 C1 |
A3 B3 C1 |
|
A1 B1 C2 |
A2 B1 C2 |
A3 B1 C2 |
|
A1 B2 C2 |
A2 B2 C2 |
A3 B2 C2 |
|
A1 B3 C2 |
A2 B3 C2 |
A3 B3 C2 |
|
A1 B1 C3 |
A2 B1 C3 |
A3 B1 C3 |
|
A1 B2 C3 |
A2 B2 C3 |
A3 B2 C3 |
|
A1 B3 C3 |
A2 B3 C3 |
A3 B3 C3 |
Например, рисунок, а соответствует кинематической схеме A1 B2 C1.
Частный бипланетарный механизм, представленный на рисунке, б, состоит из двух (ранее рассмотренных) планетарных контуров А и С. Его возможные варианты следующие:
|
A1 C1 |
A2 C1 |
A3 C1 |
|
A1 C2 |
A2 C2 |
A3 C2 |
|
A1 C3 |
A2 C3 |
A3 C3 |
Нетрудно заметить, что указанные варианты получаются из приведенных выше путем подстановки в них В=0.
На основе данных вариантов формулу для определения числа возможных кинематических схем бипланетарного механизма можно выразить в виде В=Кn, где В―число возможных кинематических схем бипланетарного механизма; К―количество возможных кинематических схем каждого планетарного контура; n―число планетарных контуров, участвующих в бипланетарном механизме.
На рисунке, аК=3, n=3, поэтому В=33=27, что соответствует комплексу вариантов, на рисунке, бК=3,n=2, следовательно, В=32=9, что согласуется с вариантами для частного бипланетарного механизма.
Возможные варианты схем бипланетарных механизмов можно увеличивать только за счет механизмов, подобных рассмотренным. При этом в кинематической схеме происходит количественное наращивание, а не качественные изменения. Для необходимого и достаточного обьёма исследований можно ограничиться тремя контурами с их тремя возможными сцеплениями.
Литература:
- Файзиев И. Х. Вопросы киберн. и вычисл. матем. Ташкент: Фан. 1996. С. 96–103.
- Файзиев И. Х. ДАН УзССР. 1969. № 1. Институт механики и сейсмостойкости сооружений им. М. Т. Уразбаева АН УзССР УзССР 1969.№ 1.







