Пусть ![]() — компактное связанное множество,
— компактное связанное множество, ![]() - гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на
- гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на ![]() и
и ![]() — одномерное комплексное пространство. Обозначим
— одномерное комплексное пространство. Обозначим ![]() Рассмотрим ограниченную самосопряженную блочно операторную матрицу
Рассмотрим ограниченную самосопряженную блочно операторную матрицу ![]() , действующую в гильбертовом пространстве
, действующую в гильбертовом пространстве ![]() и задающуюся как
и задающуюся как
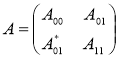 ,
,
где матричные элементы ![]() определяются по формулам
определяются по формулам
![]()
![]()
Здесь ![]()
![]() — фиксированное вещественное число,
— фиксированное вещественное число, ![]() — вещественнозначные непрерывные (ненулевые) функции на
— вещественнозначные непрерывные (ненулевые) функции на ![]() . Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирования. Отметим, что оператор
. Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирования. Отметим, что оператор ![]() можно рассмотреть как некомпактное возмущение оператора
можно рассмотреть как некомпактное возмущение оператора ![]() , рассмотренного в работе [1], где изучен число собственных значений оператора
, рассмотренного в работе [1], где изучен число собственных значений оператора ![]() . Там факты приведены без доказательства. В данной работе, в отличие от работы [1], во первых рассматривается компактный оператор, во вторых дано строгое математическое доказательства результатов о простых и бесконечно кратных собственных значений оператора
. Там факты приведены без доказательства. В данной работе, в отличие от работы [1], во первых рассматривается компактный оператор, во вторых дано строгое математическое доказательства результатов о простых и бесконечно кратных собственных значений оператора ![]() .
.
Теорема 1. Число ![]() является бесконечно кратным собственным значением оператора
является бесконечно кратным собственным значением оператора ![]() .
.
Доказательство. Рассмотрим уравнение ![]() относительно
относительно ![]() , которое эквивалентно системе уравнений
, которое эквивалентно системе уравнений
![]() . (1)
. (1)
Можно показать, что элементы подпространства
![]()
являются решениями системы уравнений (1). Видно, что
Теорема 2. Оператор ![]() может иметь не более чем 2 отрицательных и не более чем 1 положительных простых собственных значений.
может иметь не более чем 2 отрицательных и не более чем 1 положительных простых собственных значений.
Доказательство. Уравнение ![]() на собственные значения оператора
на собственные значения оператора ![]() эквивалентно системе уравнений
эквивалентно системе уравнений
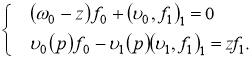
![]() (2)
(2)
Так как ![]() из второго уравнения (2) находим, что
из второго уравнения (2) находим, что
![]() (3)
(3)
где число ![]() определена по формуле
определена по формуле
![]() . (4)
. (4)
Подставляя выражение (3) для ![]() в первое уравнение системы (2) и в равенство (4) имеем, что
в первое уравнение системы (2) и в равенство (4) имеем, что
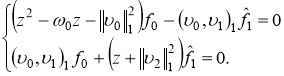 (5)
(5)
Здесь через ![]() обозначена норма в
обозначена норма в ![]() . Положим
. Положим
Система уравнений (5) имеет решение тогда и только тогда, когда детерминант этой системы равен нулю, т. е. когда ![]() .
.
Таким образом, изучение собственных значений оператора ![]() мы привели к изучению нулей полинома
мы привели к изучению нулей полинома ![]() степени 3. Заметим, что если
степени 3. Заметим, что если ![]() и
и ![]() линейно зависимы, тогда
линейно зависимы, тогда ![]() . Следовательно,
. Следовательно,
![]() и
и ![]() .
.
Пользуясь неравенством ![]() получим, что
получим, что
![]() .
.
Возможны три случая: 1) ![]() и
и ![]() ортогональны; 2)
ортогональны; 2) ![]() и
и ![]() параллельны; 3)
параллельны; 3) ![]() и
и ![]() не ортогональны и не параллельны.
не ортогональны и не параллельны.
1) Пусть ![]() и
и ![]() ортогональны. Тогда
ортогональны. Тогда ![]() . В этом случае числа
. В этом случае числа
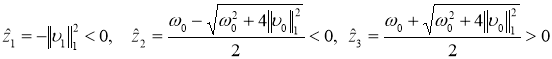
являются нулями полинома ![]() , т. е. собственными значениями оператора
, т. е. собственными значениями оператора ![]() . Отметим, что числа
. Отметим, что числа ![]() являются нулями полинома
являются нулями полинома ![]() в случае, когда
в случае, когда ![]() и
и ![]() не ортогональны.
не ортогональны.
2) Пусть ![]() и
и ![]() параллельны. Тогда
параллельны. Тогда ![]() В этом случае полином
В этом случае полином ![]() записывается в виде
записывается в виде
Отсюда видно, что числа
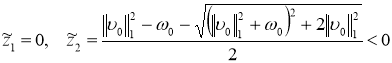 и
и 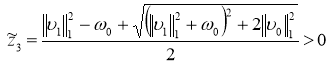
являются нулями полинома ![]() , т. е. собственными значениями оператора
, т. е. собственными значениями оператора ![]() . Заметим, что числа
. Заметим, что числа ![]() являются нулями полинома
являются нулями полинома ![]() в случае когда
в случае когда ![]() и
и ![]() не параллельны.
не параллельны.
3) Пусть ![]() и
и ![]() не ортогональны и не параллельны. Тогда имеем, что
не ортогональны и не параллельны. Тогда имеем, что ![]() Положим
Положим ![]() Тогда можно показать, что существует точки
Тогда можно показать, что существует точки ![]() ,
, ![]() ,
, ![]() которые являются нулями полинома
которые являются нулями полинома ![]() . Так как
. Так как ![]() есть полином степени 3, эти нули являются простыми. Видно, что
есть полином степени 3, эти нули являются простыми. Видно, что ![]() и
и ![]() . Теорема 2 доказана.
. Теорема 2 доказана.
Следствие. Для спектра оператора ![]() имеет место равенство
имеет место равенство
![]() .
.
Литература:
-
Р. Н. Мирзакобилов. Описание множества собственных значений одной блочной операторной матрицы размера
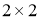 . Молодой учёный. –2016, –№ 13, –С. 50–52.
. Молодой учёный. –2016, –№ 13, –С. 50–52.







