Пусть ![]() — измеримое множество,
— измеримое множество, ![]() –декартово произведение,
–декартово произведение, ![]() - гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на
- гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на ![]() и
и ![]() — одномерное комплексное пространство.
— одномерное комплексное пространство.
Обозначим
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Тогда
![]() ,
,
![]() .
.
Определение. Гильбертово пространство
Теперь определим скалярное произведение двух элементов и норма элемента в пространствах ![]() и
и ![]() .
.
Утверждение 1. Если
![]() ,
,
то их скалярное произведение определяется по равенству:
![]() ,
,
где ![]() –есть скалярное произведение в гильбертовом пространстве
–есть скалярное произведение в гильбертовом пространстве ![]() , т. е.
, т. е.
![]() ,
,
![]() .
.
Утверждение 2. Для любых произвольных элементов
![]()
имеет место равенство
![]() .
.
Пример 1. Пусть ![]() ,
, ![]() и
и
![]() ,
,
где координаты ![]() определены следующим образом:
определены следующим образом:
![]() ,
,
![]() .
.
Тогда
![]() .
.
Утверждение 3. Норма любого элемента ![]() определяется следующим образом:
определяется следующим образом:
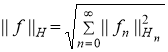 ,
,
где
![]() ,
,
![]() ..
..
Утверждение 4. Для любого элемента ![]() его норма определяется по правилу
его норма определяется по правилу
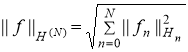 .
.
Пример 2. Пусть ![]() ,
, ![]() и
и
![]() ,
,
где координаты ![]() определены следующим образом:
определены следующим образом:
![]() .
.
Тогда
![]() ,
,
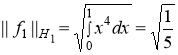 ,
,
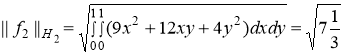 .
.
Поэтому
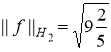 .
.
Если ![]() , то гильбертово пространство
, то гильбертово пространство ![]() называется стандартное пространство Фока [1,2] над пространством
называется стандартное пространство Фока [1,2] над пространством ![]() и обычно обозначается через
и обычно обозначается через ![]() :
:
![]() .
.
В этом случае, гильбертово пространство ![]() , т. е.
, т. е.
![]()
называется обрезанным подпространством пространства Фока, состоящей из одночастичного, двухчастичного, …, ![]() –частичного подпространства фоковского пространства. Если рассмотрим симметричные функции [2], то получается стандартное бозонное пространства Фока, в случае антисимметричных функций получается стандартное фермионное пространства Фока.
–частичного подпространства фоковского пространства. Если рассмотрим симметричные функции [2], то получается стандартное бозонное пространства Фока, в случае антисимметричных функций получается стандартное фермионное пространства Фока.
Литература:
- М.Рид, Б.Саймон. Методы современной математической физики. Т. 4. Анализ операторов. –М.: Мир. 1982, –430 С.
- R. A. Minlos, H.Spohn. The three-body problem in radioactive decay: The case of one atom and at most two photons. Topics in Statistical and Theoretical Physics, American Mathematical Society Translations, Ser. 2, V. 177, eds. R. L. Dobrushin, R. A. Minlos, M. A. Shubin, A. M. Vershik, AMS, Providence, RI, 1996, P. 159–193.







