Пусть 
гильбертово пространство и 
линейный ограниченный самосопряженный оператор. Множество всех изолированных точек спектра 
самосопряженного оператора 
, за исключением собственных значений бесконечной кратности оператора 
, будем называть дискретным спектром оператора и будем его обозначать через 
. Множество 
назывется существенным спектром оператора .
Теорема Вейля [1]. Пусть 
линейные ограниченные самосопряженные операторы и 
конечномерный оператор. Тогда имеет место равенство 
, т. е. существенный спектр оператора при конечномерных возмущениях сохраняется.
Первое применение теоремы Вейля.
Введем оператор 
модели Фридрихса, действующий в 
, как
,
где операторы 
и 
определяются по правилам
,
.
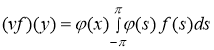Здесь 
и 
вещественнозначные непрерывные функции на 
.
Простые вычисления показывают, что
и
.
Таким образом, возмущение 
оператора 
является самосопряженным одномерным оператором. Из теоремы Вейля вытекает, что существенный спектр 
оператора 
совпадает с существенным спектром оператора 
. Известно, что
,
где числа 
и 
определяются равенствами
, 
.
Следовательно,
.
Второе применение теоремы Вейля.
Пусть
- гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на 
и 
— одномерное комплексное пространство. Обозначим 
Рассмотрим ограниченную самосопряженную обобщенную модель Фридрихса 
, действующую в гильбертовом пространстве 
и задающуюся как
,
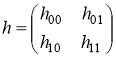где матричные элементы 
определяются по формулам
,
.
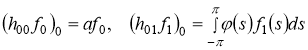Здесь 
— фиксированное вещественное число, 
— вещественнозначные непрерывные (ненулевые) функции на .
Мы знаем, что для любых элементов
,
их скалярное произведение определяется по равенству:
,
где
, 
.
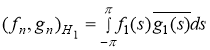С помощью этой формулы можно показать, что 
.
Положим
.
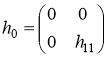Покажем, что оператор возмущения 
оператора 
является самосопряженным оператором ранга 2. По определению оператора 
имеем, что имеет вид:
.
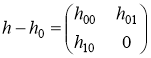Область значений оператора совпадает с множеством
.
Очевидно, что размерность этого подпространство равна 2.
Следовательно, опять из теоремы Вейля 1 вытекает, что существенный спектр оператора совпадает с существенным спектром оператора . Из одномерности пространства 
следует, что
.
Поэтому
.
Аналогичные модели изучены в работах [2, 3].
Литература:
- М.Рид, Б.Саймон. Методы современной математической физики. Т.4. Анализ операторов. М.: Мир, 1982.
- Т. Х. Расулов. Асимптотика дискретного спектра одного модельного оператора, ассоциированного с системой трех частиц на решетке. Теоретическая и математическая физика. 163:1 (2010), 34–44.
- Т. Х. Расулов. Исследование существенного спектра одного матричного оператора. Теоретическая и математическая физика. 164:1 (2010), 62–77.
