Модель Базыкина — Свирежева «хищник — жертва» обобщается на линейный ареал. Проводится анализ устойчивости стационарных решений нелинейных дифференциальных уравнений для различных граничных условий. Построение решений в области неустойчивости осуществляется с применением вариационного метода и метода конечных разностей.
Ключевые слова: популяция, краевые задачи, математическое моделирование
Введение. Математические модели «хищник-жертва», за основу которых берется модель Лотка и Вольтерра [6], как правило, представлены задачей Коши для системы обыкновенных дифференциальных уравнений. Модель Вольтера объясняет периодические изменения численности популяций, наблюдаемые в природе [4, 29]. Колебания численности возникают под действием внешних факторов и от изменения внутренних взаимоотношений между популяциями. Периодичность колебаний зависит от механизмов регуляции численности популяции, особенностей видов, от условий их существования. Последователями Вольтерра были разработаны математические модели, учитывающие более сложные взаимоотношения в системе «хищник-жертва» такие, как, например, внутривидовую конкуренцию у жертвы, нелинейный характер переработки пищевого ресурса хищником, территориальное распределение особей, направленное движение хищника за жертвой, особенности роста численности на начальной стадии своей эволюции [1, 2, 7, 16, 20, 49, 52]. Принципы построения математических моделей взаимодействующих популяций стали успешно применяться и при разработке математических моделей различных живых [3, 10, 11, 14, 22, 39, 40, 41, 46, 50] и социальных систем [15, 25, 30–36,].
Вольтера не учитывали пространственного распределения особей. Как следует из анализа результатов полевых наблюдений особи популяции на территории распределены не равномерно [4, 23, 24, 27, 38]. При разработке математических моделей для распределенных по территории особей популяций используется гипотеза о случайном их перемещении [8, 9, 26], а сами модели представляются начально-краевой задачей для системы нелинейных дифференциальных уравнений в частных производных [5, 12, 17–19, 37, 42–44, 48]. Ниже в рамках модели Свирежева-Базыкина хищник-жертва дается объяснение возникновения колебаний численности популяций и неравномерного расселения особей на территории.
Обобщенная модель Базыкина-Свирежева. Динамика численности хищника и жертвы в модели Вольтерра [2, 6, 20, 50] описывается системой двух дифференциальных уравнений
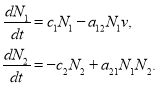 (1)
(1)
В этих уравнениях ![]() и
и ![]() — численности популяций жертвы и хищника соответственно,
— численности популяций жертвы и хищника соответственно, ![]() ,
, ![]() ,
, ![]() ,
, ![]() — константы. В окрестности стационарной точки системы уравнений (1)
— константы. В окрестности стационарной точки системы уравнений (1) ![]() ,
, ![]() происходят периодические колебания с частотой
происходят периодические колебания с частотой ![]() [2, 20]. При этом независимо от значений, которые принимают константы, стационарная точка остается центром.
[2, 20]. При этом независимо от значений, которые принимают константы, стационарная точка остается центром.
Обобщение модели Базыкина-Свирежева [2, 20] на линейный ареал с учетом «случайности» движения особей приводит к системе дифференциальных уравнений в частных производных [20]
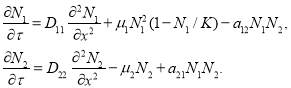 (2)
(2)
В этих уравнениях ![]() и
и ![]() — линейные плотности численности жертвы и хищника,
— линейные плотности численности жертвы и хищника, ![]() ,
, ![]() ,
, ![]() ,
, ![]() — константы, характеризующие скорости изменения численности хищника и жертвы,
— константы, характеризующие скорости изменения численности хищника и жертвы, ![]() и
и ![]() — параметры, характеризующие подвижности особей в популяциях хищника и жертвы,
— параметры, характеризующие подвижности особей в популяциях хищника и жертвы, ![]() — емкость среды обитания жертвы. В этой модели учитывается внутривидовая конкуренция у жертвы и гиперболический рост численности малочисленной популяции [2].
— емкость среды обитания жертвы. В этой модели учитывается внутривидовая конкуренция у жертвы и гиперболический рост численности малочисленной популяции [2].
Система уравнений (2) заменой переменных
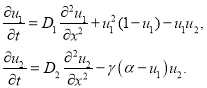 (3)
(3)
Общая численность популяций на отрезке в момент времени ![]() подсчитывается по формулам
подсчитывается по формулам
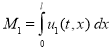 ,
, 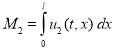 .
.
К этой системе уравнений необходимо добавить граничные и начальные условия. В качестве граничных условий для отрезка длиной ![]() рассматриваются два варианта. Первый:
рассматриваются два варианта. Первый:
при ![]() и
и ![]() :
: ![]() ,
, ![]() (4)
(4)
и второй
при ![]() :
: ![]() ,
, ![]() и при
и при ![]()
![]() ,
, ![]() .(5)
.(5)
В дальнейшем будет рассматриваться отрезок единичной длины.
Точечная модель. При ![]() и
и ![]() система уравнений (3), принимающая вид
система уравнений (3), принимающая вид
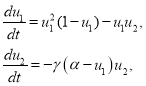 (6)
(6)
имеет две нетривиальные стационарные точки:
1. ![]() ,
, ![]() .
.
2. ![]() ,
, ![]() .
.
Первая стационарная точка при выполнении неравенства ![]() будет устойчивой, поскольку собственные значения матрицы Якоби
будет устойчивой, поскольку собственные значения матрицы Якоби ![]() и
и ![]() правой части уравнений (6) будут отрицательными.
правой части уравнений (6) будут отрицательными.
Вторая стационарная точка имеет физический смысл, при выполнении неравенства ![]() . Собственные значения матрицы Якоби в этом случае являются корнями квадратного уравнения
. Собственные значения матрицы Якоби в этом случае являются корнями квадратного уравнения
![]() .(7)
.(7)
При ![]() это уравнение в случае выполнения неравенства
это уравнение в случае выполнения неравенства 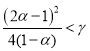 будет иметь пару комплексно сопряженных корней с отрицательной вещественной частью, в противном случае оба корня будут отрицательными. Эта стационарная точка в рассматриваемом диапазоне изменения параметра
будет иметь пару комплексно сопряженных корней с отрицательной вещественной частью, в противном случае оба корня будут отрицательными. Эта стационарная точка в рассматриваемом диапазоне изменения параметра ![]() будет устойчивой. При выполнении неравенств
будет устойчивой. При выполнении неравенств ![]() уравнение (7) будет иметь корни с положительной вещественной частью. В этом случае вторая стационарна точка будет неустойчивой.
уравнение (7) будет иметь корни с положительной вещественной частью. В этом случае вторая стационарна точка будет неустойчивой.
Таким образом, при выполнении неравенств ![]() все три стационарные точки могут быть неустойчивыми. При
все три стационарные точки могут быть неустойчивыми. При ![]() , как это следует из (6), производная
, как это следует из (6), производная ![]() отрицательна. Потому функция
отрицательна. Потому функция ![]() не может возрастать до бесконечности и, начиная с какого-то момента времени, станет убывающей функцией. Поэтому колебания в системе «хищник-жертва» в рассматриваемой модели могут возникнуть только при выполнении неравенства
не может возрастать до бесконечности и, начиная с какого-то момента времени, станет убывающей функцией. Поэтому колебания в системе «хищник-жертва» в рассматриваемой модели могут возникнуть только при выполнении неравенства ![]() . Результаты численного решения уравнений (6) в виде зависимостей искомых функций от времени при значении
. Результаты численного решения уравнений (6) в виде зависимостей искомых функций от времени при значении ![]() и начальных данных
и начальных данных ![]() и
и ![]() приведены на рис. 1, а для
приведены на рис. 1, а для ![]() — на рис. 2.
— на рис. 2.
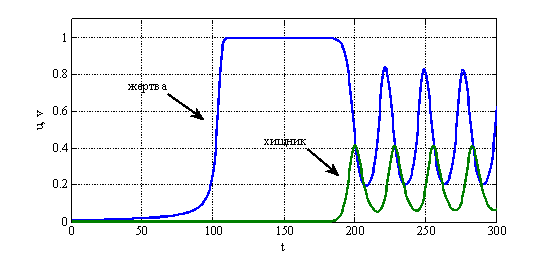
Рис. 1.
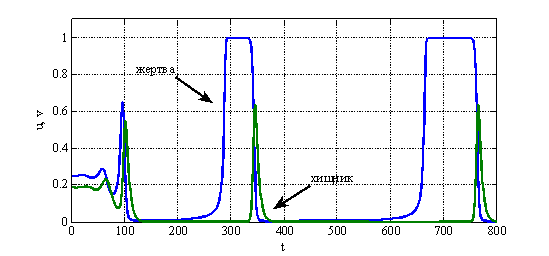
Рис. 2.
Параметр ![]() во втором уравнении в (6) представляет собой удельную скорость смертности хищника. Потому модель Базыкина — Свирежева в отличие от модели Лотка и Вольтерра «чувствительна» к смертности хищника. То есть если в системе по каким-то причинам изменяется значение
во втором уравнении в (6) представляет собой удельную скорость смертности хищника. Потому модель Базыкина — Свирежева в отличие от модели Лотка и Вольтерра «чувствительна» к смертности хищника. То есть если в системе по каким-то причинам изменяется значение ![]() , то в зависимости от ее текущего состояния, могут, либо возникнуть колебания (рис. 1, рис. 2), либо прекратиться. Возможна и гибель обеих популяций при высокой смертности хищника.
, то в зависимости от ее текущего состояния, могут, либо возникнуть колебания (рис. 1, рис. 2), либо прекратиться. Возможна и гибель обеих популяций при высокой смертности хищника.
Устойчивость стационарных решений. Стационарные решения уравнений (6) являются и решениями уравнений (3) при граничных условиях (4), а тривиальное решение и при граничных условиях (5). Линеаризация уравнений (3) в окрестности этих решений приводит к системе линейных уравнений относительно малых возмущений ![]() и
и ![]()
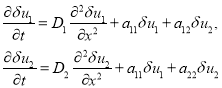 (8)
(8)
в которой в первой стационарной точке
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
а во второй
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Решение уравнений (8), удовлетворяющее граничным условиям (4) ищется в виде рядов Фурье
![]() ,
, ![]() .
.
Подстановка этих выражений в (8) приводит к системе уравнений для функций ![]() и
и ![]()
![]()
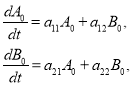 (9)
(9)
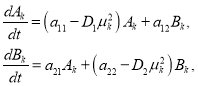
![]() (10)
(10)
где ![]() .
.
Условия устойчивости первой стационарной точки при выполнении неравенств ![]() для системы уравнений (9) совпадают с условиями устойчивости для «точечного» решения. Собственные значения матрицы правой части уравнений (10) являются корнями уравнения
для системы уравнений (9) совпадают с условиями устойчивости для «точечного» решения. Собственные значения матрицы правой части уравнений (10) являются корнями уравнения
![]() ,
,
которое и при всех (![]() ) значениях
) значениях ![]() будет иметь корни с отрицательной вещественной частью. То есть стационарное
будет иметь корни с отрицательной вещественной частью. То есть стационарное ![]() ,
, ![]() при
при ![]() будет устойчивым.
будет устойчивым.
Во второй стационарной точке собственные значения матрицы правой части уравнений (10) являются корнями уравнения
![]() .(11)
.(11)
Корни этого уравнения будут иметь отрицательные вещественные части при выполнении неравенств ![]() . В этом случае решение
. В этом случае решение ![]() ,
, ![]() уравнений (8) будет устойчивым. При выполнении неравенства
уравнений (8) будет устойчивым. При выполнении неравенства ![]() система уравнений (8) будет неустойчивой, поскольку неустойчивой будет система уравнений (9).
система уравнений (8) будет неустойчивой, поскольку неустойчивой будет система уравнений (9).
При значениях ![]() близких к нулю уравнение (11) с точностью до величин порядка малости будет иметь своими корнями
близких к нулю уравнение (11) с точностью до величин порядка малости будет иметь своими корнями
![]() и
и ![]() .
.
То есть в области малых значений параметра
![]() .
.
Это квадратное уравнение относительно ![]() при выполнении неравенств
при выполнении неравенств ![]() будет иметь положительный корень, если выполняется неравенство
будет иметь положительный корень, если выполняется неравенство
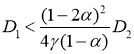 ,
,
которое является одним из условий существования периодических по пространственной переменной решений. Таким образом, неустойчивость системы уравнений (10) означает, что при малых значениях параметра ![]() могут возникать периодические по пространственной переменной решения системы уравнений (3).
могут возникать периодические по пространственной переменной решения системы уравнений (3).
Нелинейные уравнения. Решение уравнений (3) представляется для случая граничных условий (5) в виде отрезков рядов Фурье
![]() (
(![]() ).(12)
).(12)
Уравнения для функций ![]() (
(![]() ) и
) и ![]() (
(![]() ) строятся с применением метода Бубнова-Галеркина [21]. После подстановки выражений (12) в уравнения (3), умножения первого уравнения на
) строятся с применением метода Бубнова-Галеркина [21]. После подстановки выражений (12) в уравнения (3), умножения первого уравнения на ![]() (
(![]() ), а второго на
), а второго на ![]() (
(![]() ), и интегрирования их по промежутку
), и интегрирования их по промежутку ![]() будет получена система обыкновенных дифференциальных уравнений
будет получена система обыкновенных дифференциальных уравнений
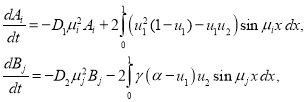 (13)
(13)
(![]() ,
, ![]() ).
).
Для частного случая ![]() и
и ![]() ,
, ![]() и
и ![]() из (13) следует система уравнений для
из (13) следует система уравнений для ![]() и
и ![]()
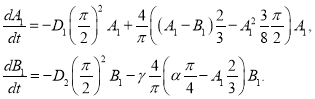 (14)
(14)
В нетривиальной стационарной точке этой системы уравнений
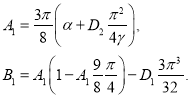 (15)
(15)
Определитель матрицы Якоби правой части уравнений (14) в стационарной точке положителен, а знак суммы собственных значений совпадает со знаком выражения
![]() . Поэтому, с учетом (15), при выполнении неравенства
. Поэтому, с учетом (15), при выполнении неравенства
![]()
стационарная точка (15) будет неустойчивой. То есть колебания в системе могут возникнуть при меньших значениях параметра ![]() чем это достигается в случае точечной модели.
чем это достигается в случае точечной модели.
Из (15) следует, что ![]() растет с ростом
растет с ростом ![]() ,
, ![]() уменьшается с ростом
уменьшается с ростом ![]() . То есть увеличение подвижности особей хищника приводит к увеличению численности жертвы, а рост подвижности жертвы сопровождается уменьшением численности хищника. При больших значениях
. То есть увеличение подвижности особей хищника приводит к увеличению численности жертвы, а рост подвижности жертвы сопровождается уменьшением численности хищника. При больших значениях ![]() эта стационарная точка может не реализовываться [7, 20, 26]. Повышение подвижности хищника может сопровождаться возникновением колебаний.
эта стационарная точка может не реализовываться [7, 20, 26]. Повышение подвижности хищника может сопровождаться возникновением колебаний.
При ![]() и
и ![]() координаты стационарной точки (15)
координаты стационарной точки (15)
![]() ,
, ![]()
практически совпадают с координатами второй стационарной точки системы уравнений (6).
В отсутствие хищника (в (15)
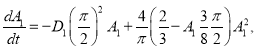
Нетривиальная стационарная точка
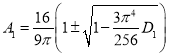
находится как положительный корень уравнения
![]() .
.
Нетривиальная точка с физическим смыслом существует, если выполняется неравенство ![]() . То есть при большой подвижности особей устойчивым стационарным решением может стать
. То есть при большой подвижности особей устойчивым стационарным решением может стать ![]() [7, 29, 36].
[7, 29, 36].
Стационарным решением нелинейных уравнений (3) с граничными условиями
при ![]() :
: ![]() ,
, ![]()
и при ![]()
![]() ,
, ![]()
являются функции ![]() и
и ![]() . Решение уравнений (3) с этими граничными условиями и начальными условиями
. Решение уравнений (3) с этими граничными условиями и начальными условиями
где ![]() и
и ![]() малые величины, строилось с применением метода конечных разностей. Использовалась равномерная сетка с числом узлов от 100 до 1000. Результаты решения на этих сетками совпадали с точностью до 1 % в максимальных отклонения. Некоторые из результатов решения для случая
малые величины, строилось с применением метода конечных разностей. Использовалась равномерная сетка с числом узлов от 100 до 1000. Результаты решения на этих сетками совпадали с точностью до 1 % в максимальных отклонения. Некоторые из результатов решения для случая ![]() ,
, ![]() ,
, ![]() ,
, ![]() приведены на рис. 3–4. На рис. 3 приведены зависимости
приведены на рис. 3–4. На рис. 3 приведены зависимости ![]() и
и ![]() , а на рис. 4 — зависимости
, а на рис. 4 — зависимости ![]() и
и ![]() в момент времени
в момент времени ![]() . Как следует из полученных численных результатов стационарное решение
. Как следует из полученных численных результатов стационарное решение ![]() ,
, ![]() не является устойчивым. При малых его возмущениях возникают колебания во времени (рис. 3) и образуются периодические по пространственной переменной структуры (рис. 4).
не является устойчивым. При малых его возмущениях возникают колебания во времени (рис. 3) и образуются периодические по пространственной переменной структуры (рис. 4).
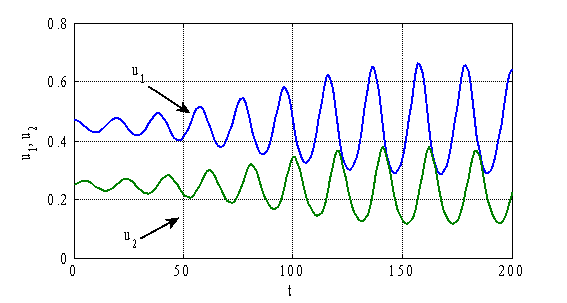
Рис. 3.
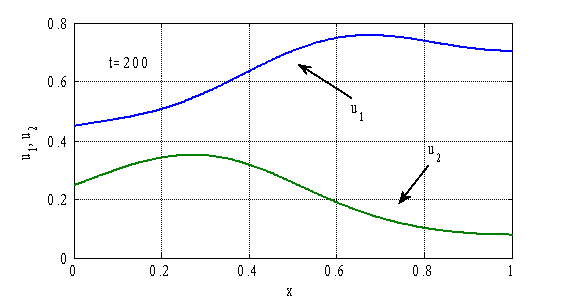
Рис. 4.
Результаты, полученные с применением метода Бубнова-Галеркина, согласуются с результатами, полученными на основе конечно-разностной аппроксимации уравнений (рис. 3–4). При построении решений можно ограничиться тремя — пятью слагаемыми в (12). На рис. 5–6 отражено значение коэффициентов ![]() (
(![]() ) и
) и ![]() (
(![]() ) в момент времени
) в момент времени ![]() . Однако, в областях значений параметров, в которых возможно существование нескольких решений, построенные численные решения с применением различных методов численного решения задач [13, 21, 45], могут не только значительно различаться между собой, но могут и не соответствовать решениям исходных нелинейных уравнений [20, 28, 47, 51].
. Однако, в областях значений параметров, в которых возможно существование нескольких решений, построенные численные решения с применением различных методов численного решения задач [13, 21, 45], могут не только значительно различаться между собой, но могут и не соответствовать решениям исходных нелинейных уравнений [20, 28, 47, 51].
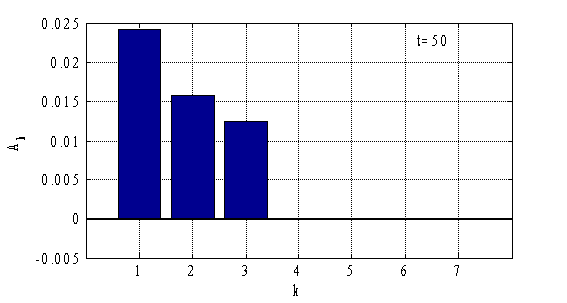
Рис. 5.
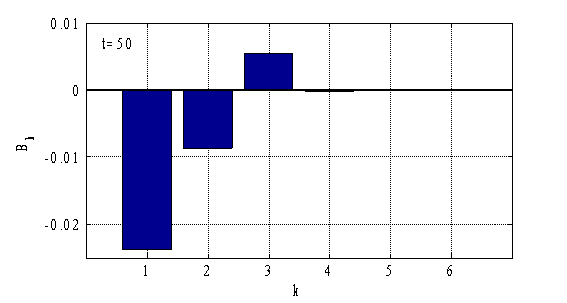
Рис. 6.
Таким образом, обобщенная на линейный ареал модель Базыкина-Свирижева хищник-жертва объяснят возможную периодичность численности популяций во времени и образование пространственных структур на ареале изменением удельной скорости гибели хищника и низкой подвижностью особей, как жертвы, так и хищника.
Работа частично поддержана грантом РФФИ 14–06–00326.
Литература:
- Апонин, Ю. М., Апонина Е. А. Математическая модель сообщества хищник — жертва с нижним порогом численности жертвы // Компьютерные исследования и моделирование. — 2009. — Т. 1. — № 1. — С. 51–56.
- Базыкин, А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий, 2003. — 368 с.
- Балыкина, Ю. Е., Колпак Е. П. Математические модели функционирования фолликула щитовидной железы // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 20–31.
- Бигон, М., Харпер Дж., Таунсенд К. Экология. Особи, популяции и сообщества: в двух томах. М.: Мир, 1989. Т. 1. — 667 с. Т. 2. — 477с.
- Будянский, А. В., Цибулин В. Г. Моделирование пространственно-временной миграции близкородственных популяций // Компьютерные исследования и моделирование. — 2011. — Т. 3. — № 4. — С. 477–488.
- Вольтерра, В. Математическая теория борьбы за существование. Москва-Ижевск: Институт компьютерных технологий, 2004. — 288 с.
- Гаврилова, А. В., Колпак Е. П. О динамике создания художественных произведений И. К. Айвазовским // Молодой ученый. — 2017. — № 1. — С. 110–117.
- Екимов, А. В. Анализ множества достижимости нелинейных управляемых систем//Естественные и математические науки в современном мире. -2014. — № 15. -С. 8–13.
- Екимов, А. В. К вопросу об эргодисческом поведении полумарковского случайного процесса // Труды математического центра имени Н. И. Лобачевского. — 2013. — Т. 46. — № 11. — С. 185–186.
- Жукова, И. В., Колпак Е. П. Математическая модель солидной опухоли // Естественные и математические науки в современном мире. — 2013. — № 13. — С. 18–25.
- Жукова, И. В., Колпак Е. П. Математические модели злокачественной опухоли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 5–18.
- Колпак, Е. П. Устойчивость и закритические состояния безмоментных оболочек при больших деформациях // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербург, 2000.
- Колпак, Е. П. Вычисления в Matlab: Учебное пособие / Казань, 2016.
- Колпак, Е. П., Балыкина Ю. Е., Котина Е. Д., Жукова И. В. Математическая модель нарушений функционирования щитовидной железы // Молодой Ученый. — 2014. — № 2(61). — С. 19–24.
- Колпак, Е. П., Габриелян Л А., Бронникова А. И., Крылова В. А. О математических моделях симбиоза // Молодой ученый. — 2015. — № 4 (84). — С. 6–14.
- Колпак, Е. П., Горбунова Е. А., Балыкина Ю. Е., Гасратова Н. А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. — 2014. — № 1 (6). — С. 28–33.
- Колпак, Е. П., Горбунова Е. А., Жукова И. В. Математическая модель популяционной волны // Естественные и математические науки в современном мире. — 2014. — № 16. — С. 25–41.
- Колпак, Е. П., Горбунова Е. А., Столбовая М. В., Балыкина Ю. Е Математическая модель логистической популяции на линейном ареале // Молодой ученый. — 2014. — № 3 (62). — С. 6–14.
- Колпак, Е. П., Горыня Е. В., Крылова В. А., Полежаев Д. Ю. Математическая модель конкуренции двух популяций на линейном ареале // Молодой ученый. — 2014. — № 12 (71). — С. 12–22.
- Колпак, Е. П., Горыня Е. В., Селицкая Е. А. О моделях А. Д. Базыкина «хищник — жертва» // Молодой ученый. 2016. № 2 (106). С. 12–20.
- Колпак, Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4. — С. 20–30.
- Колпак, Е. П., Столбовая М. В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. — 2013. — № 12 (90). — С. 230–232.
- Коробченко, М. А. Расширение ареала крота европейского (talpa europaea) в долине реки Северный Донец // Зоологический журнал. — 2009. — Т. 88. — № 4. — С. 465–472.
- Мамонтов, С. Н. Распределение по стволу дерева короеда-типографа (ips typographus, coleoptera, scolyniddae) и его энтомофагов // Зоологический журнал. — 2009. — Т. 88. — № 9. — С. 1139–1145..
- Миндлин, Ю. Б., Колпак Е. П., Балыкина Ю. Е Проблемы использования кластеров в Российской Федерации // Вестник НГУЭУ. — 2014. — № 1. — С. 22–32.
- Мятлев, В. Д., Панченко Л. А., Ризниченко Г. Ю., Терехин А. Т. Теория вероятностей и математическая статистика. Математические модели. М.: Издательский центр «Академия», 2009. — 320 с.
- Окулова, Н. М., Катаев Г. Д. Взаимосвязи «хищник-красно-серая полевка» в сообществах позвоночных животных Лапландского заповедника // Зоологический журнал. — 2007. — Т. 86. — № 8. — С. 989–998.
- Столбовая М. В., Колпак Е. П., Селицкая Е. А., Ефремова Е. А. Математическая модель распространения уссурийского полиграфа // Молодой ученый. — 2017. — № 1. — С. 124–129.
- Садыков, О. Ф., Бененсон И. Е. Динамика численности мелких млекопитающих: Концепции, гипотезы, модели. М.: Наука, 1992. — 191 с.
- Старкова, Н. В. Возрастная структура населения и повозрастная интенсивность рождений как факторы изменения уровня рождаемости в Ленинградской области // Вестник Санкт-Петербургского университета. Серия 7. Геология. География. — 2008. — № 3. — С. 98–106.
- Старкова, Н. В. Особенности демографического развития районов Ленинградской области // Вестник Санкт-Петербургского университета. Серия 7. Геология. География. — 2007. — № 4. — С. 87–97.
- Старкова, Н. В. Особенности социально-экономического развития приграничных муниципальных районов ленинградской области // В сборнике: Стратегия развития приграничных территорий: традиции и инновации Материалы международной научно-практической конференции. 2014. — С. 350–359.
- Старкова, Н. В. Современные особенности миграции населения Ленинградской области // В сборнике: Стратегия развития приграничных территорий: традиции и инновации Материалы II международной научно-практической конференции. 2015. — С. 173–180.
- Старкова, Н. В. Тенденции и факторы миграции в странах Европы // В сборнике: География и геоэкология на службе науки и инновационного образования материалы XI Международной научно-практической конференции, посвященной Всемирному Дню Земли и 100-летию заповедной системы России. 2016. — С. 154–157.
- Старкова, Н. В., Ложкинс А. Кластеризация стран Европы по демографическим признакам // Молодой ученый. — 2016. — № 9 (113). — С. 418–426.
- Трубецков, Д. И. Феномен математической модели Лотки-Вольтерры и сходных с ней // Известия высших учебных заведений. Прикладная нелинейная динамика. — 2011. — Т. 19. — № 2. — С. 69–88.
- Тютюнов, Ю. В. Пространственная модель развития устойчивости насекомых-вредителей к трансгенной инсектицидной сельскохозяйственной культуре // Биофизика. — 2007. — Т. 52. — № 1. — С. 95–113.
- Уморин, П. П. Роль хищников в устойчивом существовании нескольких видов водорослей // Биология внутренних вод. — 2009. — № 1. — С. 3–7.
- Чекунова, Е. М Генетика биосинтеза хлорофилла: темновой и светозависимый пути // Экологическая генетика. — 2010. — Т. VIII. — № 3. — С. 38–51.
- Чекунова, Е. М., Савельева Н. В Ген lts3 контролирует светонезависимый биосинтез хлорофилла у зеленой водоросли Rhlamydomonas Reinhardtii // Экологическая генетика. -2010. -Т. VIII. -№ 2. -С. 35–44.
- Abrams, P. A., Chad E., Brassil C. E., Robert D., Holt R. D. Dynamics and responses to mortality rates ofcompeting predators undergoing predator–prey cycles // Theoretical Population Biology. — 2003. — V. 64. — P. 163–176.
- Garvie, M. R. Finite-difference schemes for reaction–diffusion equations modeling predator–prey interactions in Matlab // Bulletin of Mathematical Biology. — 2007. — V. 69. — P. 931–956.
- Ge w., Gui z. The effect of harvesting on a predator–prey system with stage structure // Ecological Modelling. — 2005. — V. 187. — P. 329–340.
- Jones, L. E., Ellner S. P Evolutionary Tradeoff and Equilibrium in an Aquatic Predator–Prey System // Bulletin of Mathematical Biology. — 2004. — V. 66. — P. 1547–1573.
- Kabrits, S.A., Slepneva L. V. Small nonsymmetric oscillations of viscoelastic damper under massive body action // Вестник Санкт-Петербургского университета. Серия 1. Математика. Механика. Астрономия. 1998. Т. 2. № 1998. С. 78
- Kolpak, E. P., Gorynya E.V Mathematical models of ecological niches search // Applied Mathematical Sciences. — 2016. — Т. 10. — № 37–40. — С. 1907–1921.
- Kolpak, E. P., Maltseva L. S., Ivanov S. E. On the stability of compressed plate // Contemporary Engineering Sciences. — 2015. — Т. 8. — № 20. — С. 933–942.
- Kolpak, E. P., Stolbovaia, M.V., Frantsuzova, I. S. Mathematical models of single population // Global Journal of Pure and Applied Mathematics. — 2016. 12 (4), — pp. 2923–2934.
- Lopez-Sanchez, J.F., Alhama F., Gonzalez-Fernandez C.F Introduction and permanence of species in a diffusive Lotka-Volterra system with time-dependent coefficients // Ecological Modelling. — 2005. — V. 183. — P. 1–9.
- Murray, D. D. Mathematical biology. N. Y. Springer. 2002, — 551 p.
- Pronina, Y.G., Sedova O. S., Kabrits S. A. On the applicability of thin spherical shell model for the problems of mechanochemical corrosion // В сборнике: AIP Conference Proceedings 2015. С. 300008.
- Wang, W., Takeuchi Y. Adaptation of prey and predators between patches // Journal of Theoretical Biology. — 2009. — V. 258. — P. 603–613.







