Способ вращения геометрической фигуры вокруг оси плоскости проекций

В качестве оси вращения принимается горизонтальный или вертикальный след плоскости в общем положении (рис. 1), данная плоскость вращается вокруг определенного следа, и прикладывается к одной из плоскостей проекции. Если в качестве оси вращения принимается горизонтальный след плоскости, можно приложить с плоскостью горизонтальной проекции. Также, вращая плоскость вокруг фронтального следа, можно её приложить к плоскости фронтальной проекции. Способом приложения плоскостей к соответствующим плоскостям проекций можно определить действительный размер геометрической фигуры, либо в указанной плоскости общего положения можно создать любую требуемую геометрическую фигуру. В рис. 2-а иллюстрировано вращение плоскости Q в общем положении Q_N вокруг горизонтального следа и его приложение к плоскости H. Так как горизонтальный след плоскости принят в качестве оси вращения, его положение не меняется [1, 4]. Для приложения данной плоскости к плоскости Н достаточно приложить какую-либо точку этой плоскости к плоскости Н. В качестве данной точки можно принять точку В, принадлежащую к фронтальному следу плоскости. Ось вращения данной точки вращается на плоскости М перпендикулярной Q_N по дуге AA₁ до её пересечения со следом M_N.

В результате, если соединить образовавшуюся точку A₁ с P_X, получаем приложение плоскости P к плоскости H. При данном приложении плоскости принадлежащая ей геометрическая фигура прилагается к плоскости H, и проецируется в действительных размерах. На схеме необходимо вращать плоскость P (P_N, P_V) вокруг следа P_N, и определить действительный радиус вращения для приложения к плоскости Н (рис. 2-б). Как известно, радиус вращения является перпендикулярным к оси вращения плоскости. Согласно свойству проецирования прямого угла, с проекции A' точки A (A', A''), полученной на следе P_V проводится перпендикуляр следу P_N, и определяются точки O' и O''. Образованные на схеме O'A' и O''A'' являются проекциями радиуса вращения, а O' A₀ является действительным размером радиуса [2, 3].

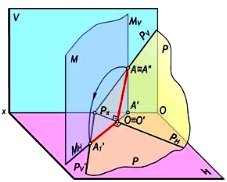
Рис. 1.

Из рис. 2-а можно определить, что при вращении плоскости Q вокруг следа Q_N и его приложении к плоскости Н отрезок Q_X B₁ относящийся к следу Q_V равен Q_X B''–Q_X B₁. Значит, для приложения плоскости Q (Q_N, Q_V) к плоскости H (рис. 3-б) взяв точку B ≡ B'' на следу Q_V и рисуя дугу по радиусу Q_X B'' от центра Q_X, определяется точка B₁ пересечения плоскости M со следом M_N. Затем с точек B₁ и Q_X проводится след Q_V1. Аналогично можно приложить плоскость R (R_H, R_V) к плоскости V (рис.3). Как видно из схемы R_H для плоскости R, при вращении плоскости P вокруг следа P_N отрезок P_X A будет равен отрезку P_XA₁ ga. На горизонтальном следе берем точку A и определяем радиус вращения P_X A', и вращая след плоскости P_N вокруг плоскости P_V, смыкаем плоскости. Для определения действительных размеров геометрической фигуры относящейся к данной плоскости используется способ приложения характерных точек фигуры к плоскости проекции. Например, действительные размеры ∆ABC (A'B'C', A''B''C'') относящегося к плоскости Q(Q_N, Q_V) определяется путём приложения точек A, B и C к плоскости V.

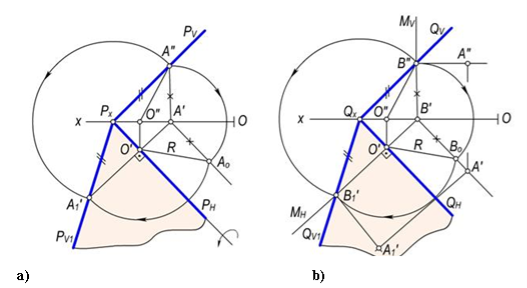
Рис. 2.

Также может быть рассмотрена задача создания проекций геометрической фигуры определенного размера и формы, расположенной в плоскости общего положения. Для решения данной задачи плоскость общего положения прилагается к плоскости проекций, и требуемая геометрическая фигура отображается на данной плоскости. После чего полученная плоскость вновь приводится в общее положение.

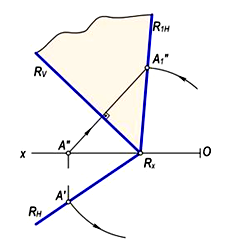
Рис. 3.

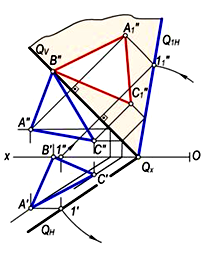
Рис. 4.

Например, дано положение приложения плоскости P к плоскости H, следы P_V, P_V1 и находящаяся на них окружность с радиусом R.

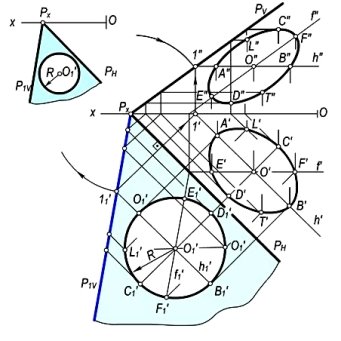
Рис. 5.

Для создания проекций данной окружности (рис. 5) на плоскости P от центра плоскости проводится горизонталь h'₁ и определяется точка 1'₁. От данной точки проводится перпендикуляр к следу P_N и на оси проекций Ox определяется точка 1'. Проводится проекция h' от h'₁. После чего от центра P_x проводим фронтальную f'₁ плоскости P_x1'₁ параллельно от центра O'₁ к P_1V и производим проекции E', E'' и F', F'' для точек E'₁ и F'₁. Аналогично проекции точек L'₁ и T'₁, C'₁ и D'₁ определяются при помощи горизонтальных плоскостей. При соответствующем соединении одноименных проекций данных точек получаем горизонтальную и фронтальную проекции окружности (в виде эллипсоида).

Литература:

1. Муродов Ш. К. и др. Чизма геометрия. — Т.: Иктисод-молия, 2008.
2. Ёдгоров Ж. Ё. и др. Геометрик ва проекцион чизмачилик. — Т.: Янги аср авлоди, 2008.
3. Ёдгоров Ж.Ё. Чизма геометрия. — Т.: 2006.
4. Чекмарев А. А. Начертательная геометрия и черчение. Учебник для вузов — М.: Владос, 2002.