Интеграция опыта по физике и математике с нацеленностью на исследование как фактор успешного освоения учащимися технической механики в учреждении СПО



Условия равновесия механических систем, обусловленные состоянием покоя или прямолинейным равномерным движением, представляют предмет исследования статики — раздела механики. В школе механические явления изучаются на уроках физики. Проведем краткий анализ содержания предмета «Физика» в основной школе с целью выявления уровня готовности учащихся к изучению дисциплины «Техническая механика» в образовательной организации среднего профессионального образования.

Уже в 7-м классе у школьников формируется представление о взаимодействии тел на примерах действия одного тела на другое. Внимание при этом заостряется на обоюдном действии тел друг на друга, что указывает на двусторонность действия, а значит, на их взаимодействие. На знакомых из жизни примерах учащиеся подводятся к понятию «сила», как мере взаимодействия тел. Указываются признаки действия силы на тело связанные с изменением значения скорости или направления движения, размеров или формы тела. Отмечается, что сила является величиной векторной и характеризуется точкой приложения, направлением и значением (модулем). Раскрывается смысл единицы измерения силы — ньютон. Устанавливаются связи между силой тяжести, весом тела и массой, силой упругости и изменением длины тела. Называются причины возникновения силы трения. Производится измерение силы с помощью динамометра. И даже выполняется сложение двух сил, правда в частном случае, когда силы направлены по одной прямой. Поэтому равнодействующая сила представляет арифметическую сумму значений исходных сил [8].

Важные сведения, способствующие дальнейшему развитию представлений школьников о статических явлениях, рассматриваются в 9-м классе при обосновании и формулировании понятия «материальная точка», а также первого и третьего законов Ньютона [9]. Хотя в приводимых примерах и предлагаемых для решения заданиях векторы сил по-прежнему остаются коллинеарными.

В совокупности перечисленные знания и умения, приобретаемые учащимися на уроках физики, составляют базовую основу для последующего изучения статики в курсе технической механики выпускниками основной школы, продолжающими обучение профессиям или специальностям технического профиля в учреждениях среднего профессионального образования. Следует также отметить, что при изучении геометрии в 9-м классе школьники получают необходимую для оперирования векторами подготовку. В частности, учатся откладывать вектор от данной точки, знакомятся с правилами сложения (способом треугольника, параллелограмма, многоугольника) и вычитания векторов, выполняют умножение вектора на число, применяют векторы в решении задач с геометрическим содержанием [4].

В технической механике принят аксиоматико-дедуктивный подход к изложению материала, придающий дисциплине научную строгость. Опыт, приобретенный человечеством в результате длительных наблюдений и прошедший проверку практикой, составляет исходные положения, лаконично сформулированные в виде аксиом. На основе аксиом статики логично выстраиваются рассуждения, доказываются теоремы, формулируются выводы и решаются задачи. Структура раздела статика, кроме исходных положений и аксиом, включает плоские системы сходящихся и параллельных сил, момент силы и систему пар сил, плоскую систему произвольно расположенных сил и пространственную систему сил, трение и центр тяжести.

Важное место в методике обучения технической механике отводится решению задач. Не случайно в учебниках, наряду с изложением теоретического материала, разбираются примеры, а в сборниках задач и руководствах по решению задач предлагаются задания для самостоятельного выполнения [2; 3; 7; 10; 16 и др.]. К примеру, в учебнике Е. М. Никитина предложено подробное решение 118 типовых задач, «занимающих около 25 % объема книги» [7, с. 8]. Овладение методами решения учебных задач составляет одну из главных задач изучения технической механики и раздела статика в учреждениях среднего профессионального образования.

Основные виды задач статики связаны с определением реакций, распространенных в технических конструкциях связей и опор нагруженных балок. В задачах на определение идеальных связей в плоской системе сходящихся сил исходные условия, в общем случае, можно привести к виду, когда известны активная сила и направления реакций. Выберем в качестве активной силы системы силу тяжести G, а направления реакций отложим от вертикальной оси (углы α и β) по лучам a и b из точки O (рис. 1).

По исходным данным можно представить замкнутый силовой треугольник (рис. 2) и, воспользовавшись теоремой синусов, установить зависимости для реактивных сил: , , .

Решение задачи и последующую проверку полученного результата можно осуществить введением прямоугольной или косоугольной системы координат, а также использованием свойств геометрических фигур [13; 14 и др.]. При этом заслуживает исследовательского интереса осмысление влияния значения силы G и углов α и β на реакции R_a и R_b.

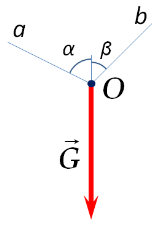
Рис. 1. Общий вид исходных условий задачи по определению реакций идеальных связей.

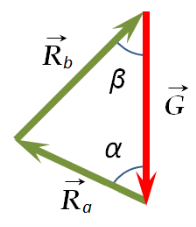
Рис. 2. Силовой треугольник

Очевидно, что изменение G при сохранении α и β приводит к пропорциональному изменению R_a и R_b. Треугольники сил остаются подобными. Иным образом влияет изменение угла α или β при постоянном значении другого из них и силы G на реакции связей R_a и R_b. Прямая или обратная пропорциональность между реактивными силами в этом случае не проявляется. В силовом треугольнике общая точка векторов R_a и R_b меняет местоположение, причем таким образом, что при изменении α она скользит по линии действия R_b, а при изменении β — по линии действия R_a.

На векторах сил системы может быть построен другой треугольник, если G, R_a и R_b отложить из точки пересечения линий их действия (точки O) и отрезками соединить конечные точки этих векторов (рис. 3).

Докажем теорему о неколлинеарности векторов уравновешенной плоской системы трех сходящихся сил, выходящих из общей точки.

Отличительная особенность исследуемого треугольника заключается в том, что векторы G, R_a и R_b, согласно геометрическим условиям равновесия, образуют замкнутый треугольник (рис. 2). Поэтому любой из этих векторов является векторной суммой двух других: ; ; . Именно данная особенность обуславливает причину, по которой векторные суммы и соответствующие им векторы системы сил располагаются на одних линиях действия: ; ; (рис. 4).

Достроим треугольник, полученный соединением конечных точек векторов G, R_a и R_b, выходящих из точки O (рис. 3) до шестиугольника, откладывая вспомогательные векторы G, R_a и R_b (пунктирные стрелки) из соответствующих вершин (рис. 5). Внутри шестиугольника можно выделить три параллелограмма, которые основываются на векторах сил (сплошные стрелки), как сторонах, и граничащие между собой по этим векторам. Основанием утверждать, что данные фигуры именно параллелограммы, позволяет сохранение параллельности и длин при отложении вспомогательных векторов (пунктирные стрелки).

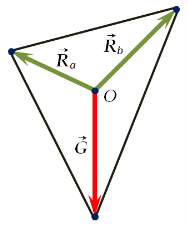
Рис. 3. Треугольник, построенный на конечных точках векторов G, R_a и R_b, отложенных от точки пересечения линий их действия

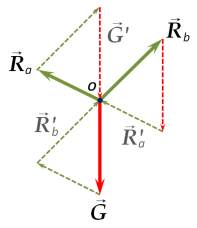
Рис. 4. Особенность векторов плоской уравновешенной системы сходящихся сил: общие линии действия у ; ; .

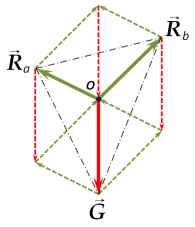
Рис. 5. Шестиугольник, полученный из треугольника на конечных точках векторов G, R_a и R_b, отложенных из точки O

В каждом параллелограмме проходят диагонали: пунктирные стрелки и штрихпунктирные линии. По свойству параллелограмма диагонали точкой пересечения делятся пополам. При этом каждый из векторов G, R_a и R_b (сплошные стрелки) расположен на одной прямой с соответствующим дополнительным вектором (пунктирные стрелки) в силу параллельности построений. Значит, на линиях действия векторов G, R_a и R_b (сплошные линии) находятся медианы анализируемого треугольника (стороны выполнены штрихпунктирными линиями).

Предположим, что какие-либо два или все векторы плоской уравновешенной системы трех сходящихся сил коллинеарны. В этом случае соответствующие медианы треугольника должны быть параллельными. Но в сходящейся системе сил, когда силовой треугольник не вырожден, такое невозможно, поскольку у трех медиан треугольника имеется общая точка и только одна. А у параллельных прямых общих точек нет или их бесконечное множество, если прямые совпадают. В результате возникает противоречие между выдвинутым предположением и полученным в ходе рассуждений заключением. Следовательно, высказанное предположение неверно.

Таким образом, векторы уравновешенной плоской системы трех сходящихся сил, выходящие из точки пересечения линий их действия, неколлинеарны, т. е. не могут быть параллельными, что и требовалось доказать.

Из теоремы о неколлинеарности векторов сил вытекают важные следствия.

Следствие 1. Линии действия векторов сил рассматриваемых систем не совпадают.

Поскольку векторы уравновешенной плоской системы трех сходящихся сил, выходящих из общей точки, располагаются на медианах, а они не могут быть параллельными, то исключается и возможность расположения векторов сил на одной прямой.

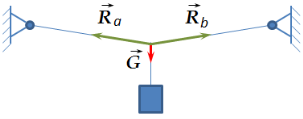
Примером из техники, подтверждающим первое следствие, может быть гибкая связь (канат, торс, цепь) под внешним грузом G. После нагружения в такой системе угол между возникающими реактивными силами R_a и R_b не будет развернутым (рис. 6 а и б). А если груз приложить к балке (абсолютно твердому телу), то система сходящихся сил превращается в систему параллельных сил (рис. 7) и исследуется другими правилам.

а)

б)

Рис. 6. Гибкая связь: а) без нагрузки (с пренебрежением собственным весом); б) под нагрузкой (пример системы сходящихся сил)

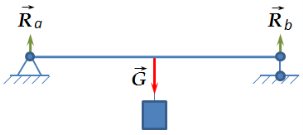
Рис. 7. Балка (абсолютно твердое тело) под нагрузкой (пример системы параллельных сил)

Следствие 2. Точка пересечения линий действия векторов сил анализируемых систем представляет центр тяжести (центроид или барицентр) треугольника, построенного на конечных точках векторов этих сил, когда они выходят из данной общей для них точки (рис. 3).

Второе следствие из теоремы о неколлинеарности векторов представляет одно из свойств медиан треугольника.

Теорема о неколлинеарности векторов раскрывает и помогает осознать причинно-следственные связи, существующие в плоской системе сходящихся сил. А следствия из данной теоремы позволяют выполнить предварительную проверку геометрического решения задач статики на определение реакций идеальных связей и быстро выявить очевидные ошибки.

Проведенные в статье рассуждения полностью основываются на знаниях и умениях учащихся, приобретенных в основной школе. Эффективность интеграции опыта обучающихся по физике и математике с нацеленностью на исследование под руководством преподавателя в процессе изучения технической механики подтверждается положительными результатами нашей опытно-экспериментальной работы по активизации познавательной деятельности и развитию творческих способностей [11; 15], формированию умений рассуждать и аргументировать [5; 6], повышению качества профессионального обучения [1; 12].

Литература:

1. Masalimova, A.R., Chibakov, A.S. (2016). Experimental Analytical Model of Conditions and Quality Control of Vocational Training of Workers and Specialists. IEJME-Mathematics Education, 11(6), 1796–1808.
2. Аркуша, А.И. руководство к решению задач по технической механике: Учеб. пособ. для средних спец. учеб. заведений / А. И. Аркуша. — 5-е изд., испр. — М.: Высш. шк., 2002, — 336 с.
3. Вереина Л. И. Техническая механика: учебник для студ. учреждений сред. проф. образования / Л. И. Веренина. — 10-е изд., стер. — М.:.: Издательский центр «Академия», 2015. — 224 с.
4. Геометрия. 7–9 классы: учеб. для общеобразоват. организаций / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. — 2 изд. — М.: Просвещение, 2014. — 383 с.
5. Крылов Д. А., Чибаков А. С. Измерение и оценка развития аргументативных умений и качеств будущих квалифицированных рабочих и специалистов в процессе профессиональной подготовки // Современные проблемы науки и образования. — 2016. — № 1.; URL: http://www.science-education.ru/ru/article/view?id=24099
6. Крылов Д. А., Чибаков А. С. Развитие аргументативных качеств обучающихся методами СПР при освоении профессиональных модулей // Современные проблемы науки и образования. — 2015. — № 6; URL: www.science-education.ru/130–23911
7. Никитин Е. М. Теоретическая механика для техникумов. — 12-е изд., испр. — М.: Наука. Гл. ред. физ.-мат. лит., 1988. — 336 с.
8. Перышкин, А. В. Физика. 7 кл.: учеб. для общеобразоват. учреждений / А. В. Перышкин. — 2-е изд., стереотип. — М.: Дрофа, 2013. — 221 с.
9. Перышкин, А. В. Физика. 9 кл.: учебник для общеобразоват. учреждений / А. В. Перышкин, Е. М. Гутник. — 17-е изд., стереотип. — М.: Дрофа, 2012. — 300 с.
10. Сетков В. И. Сборник задач по технической механике: учеб. пособие для студ. учреждений сред. проф. образования / В. И. Сетков. — 8-е изд., стер.. — М.: Издательский центр «Академия», 2013. — 240с.
11. Чибаков А. С. Исследование развития познавательной активности учащихся в условиях среднего профессионального образования // Научный диалог. — 2016. — № 4 (52). — С. 395–408.
12. Чибаков А. С. К оценке качества профессионального обучения: методический аспект // Профессиональное образование. Столица. — 2016. — № 3. — С. 41–44.
13. Чибаков А. С. Метод координат в решении учебных задач статики по определению реакций идеальных связей // Школа будущего. — 2016. — № 5. — С. 134–140.
14. Чибаков А. С. Определение реакций идеальных связей в плоской системе сходящихся сил на основе свойств геометрических фигур // Глобальный научный потенциал. — 2016. — № 10 (67). — С. 28–33.
15. Чибаков А. С. Разработка учебных информационно-коммуникативных проектов на основе эвристических методов // Молодой ученый. — 2015. — № 8 (88). — Часть 10. Педагогика — С. 1067–1074.
16. Эрдеди А. А. Техническая механика: учебник для студ. учреждений сред. проф. образования / А. А. Эрдеди, Н. А. Эрдеди. — М.: Издательский центр «Академия», 2014. — 528 с.