Рассматривается вопрос о построении приближенного решения линейных обыкновенных дифференциальных уравнений четвертого порядка. Излагаются два метода: метод конечных разностей и дифференциальной прогонки с модификацией матричного варианта.
Ключевые слова: аппроксимация, единичная матрица, матричная прогонка, случайная ошибка, векторно-разностные схемы
В данной работе рассматривается вопрос о построении приближенного решения линейных обыкновенных дифференциальных уравнений четвертого порядка с переменными коэффициентами и сравнительно общими краевыми условиями. При этом авторы сочли возможным и заложить сразу два метода построения, чтобы выявить применительно к приведенным краевым задачам эффективность применения того или другого метода. Первый из них — метод конечных разностей с модификацией матричного варианта прогонки. Второй алгоритм базируется на использовании матричного варианта дифференциальной прогонки. Частный случай применения этих методов к численному решению уравнений четвертого порядка приводится в работах. [1, 3]
Постановка задачи:
Требуется определить в области [a, b] неизвестный вектор функции 
удовлетворяющей системе дифференциальных уравнений:
(1)
Записанной в матричной форме при граничных условиях
(2)
(3)
где
заданные квадратные матрицы в порядке 
; f(x) и 
– 
– мерные векторы функции, причем существует матрица 
для всех X
[a,b] а также рассматривается система дифференциальных уравнений вида
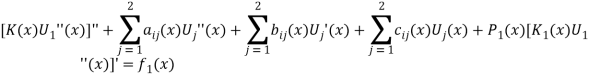(4)
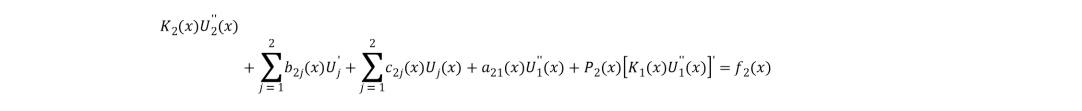(5)
Соответствующими граничными условиями
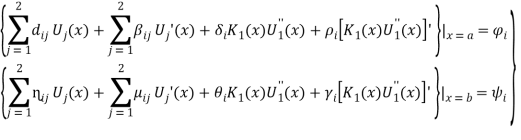(6)
Гдеi=
искомые векторы.
Будем предполагать, что на отрезке [a, b] решение задач (1)-(3), а также (4)-(6) существует и единственно. Гладкость входных данных и решения задач предположим такими, какие нам будут нужны в каждом случае.
Метод конечных разностей. Введя обозначение
(7)
уравнение (1) перепишем:
(8)
Построим равномерную сетку с шагом h:
Согласно методу баланса (1) из второго уравнения (8) с погрешностью аппроксимации 
имеем [2]
(9)
Здесь:
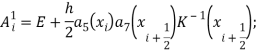
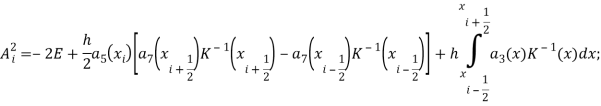
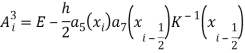
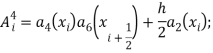
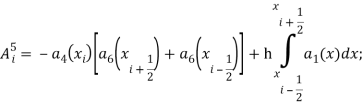
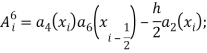
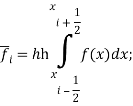
-единичная матрица.
Проделав аналогичную процедуру с первым уравнением (8) и обозначив
(10)
Представим первое уравнение (8) и уравнение (9) в виде [4]
i=1,2,…,N-1(11)
Где:
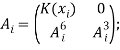
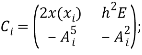
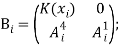
Здесь для нахождения N+1 неизвестных векторов имеем N-1 матричных уравнений, а недостающие уравнения получаем из граничных условий (2) и (3) с учетом уравнения (7), используя при зетом трехточечную аппроксимацию для значений производных 
и W'(x) c точностью 
(12)
Где:
Итак, мы полностью сформулировали разностную задачу (11) – (12), решение которой, исходя из метода матричной прогонки [4], ищем в виде
i=1,2,…,N-1(13)
Где
p,s=1,2,…,2n; 
Соответственно матричные и векторные про гоночные коэффициенты, определяемые из соотношений
(14)
Формулы для вычисления значений 
и 
, дающие возможность начать счет для про гоночных коэффициентов по формулам (14), получим так: умножим слева на уравнение (11) при i=I матрицу 
и, отнимая найденное соотношение от первого уравнения (12), приходим к равенству
(15)
Сопоставляя соотношение (15) с формулой (13) при i=I, имеем
Определив значения 
и 
для всех I, затем решая уравнения
совместно со вторим уравнением (12) получаем
Далее с помощью обратной прогонки (13) вычислим 
После этого найдем 
по формуле
Заметим, что в процессе реализации на компьютере метода матричной прогонки необходимо проверить выполнение условий [1]
которые обеспечивают устойчивость изложенного метода по отношению к случайной ошибке. При этом во всех точках 
выполняется неравенство 
Перейдем к построению численного решения дифференциальной краевой задачи (4)-(6). Легко заметить, что в этом случае после некоторых преобразований решение задачи (4)-(6) может быть сведено к описанным выше вычислительным алгоритмам.
Действительно, сделав в уравнениях (4)-(6) замену переменной 
перепишем систему (4)-(5):
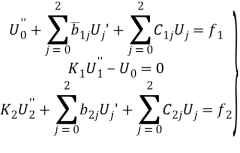(16)
С граничными условиями
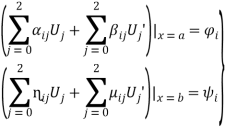(17)
Где:
Далее в задаче (16)-(17) введя обозначение:
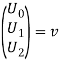(18)
Получаем:
(19)
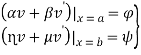(20)
Здесь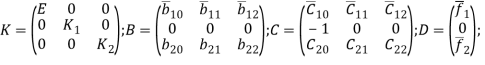 
i=1,2,3; j=0,1,2.
Теперь для задачи (19)-(20) можно применить абсолютно устойчивые векторно-разностные схемы с точностью 
предложенные И.В. Фрязиновым в Первой всесоюзной школе по численным методам математической физики в Казани 
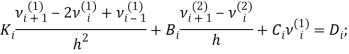
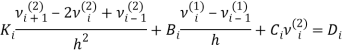
Здесь, вводя обозначения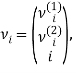 
Приходим к разностным задачам:
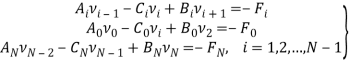(21)
Где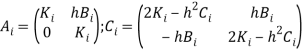 
; 
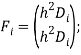
Матричная дифференциальная прогонка. В ряде случаев для построения решения задачи (1)-(3) целесообразно применение метода дифференциальной прогонки 
. Для удобства изложения рассмотрим случай (21) при 
Уравнение (1) примет вид
(22)
Имея в виду (7) и вводя в полученное выражение обозначение
из (22), имеем:
Где 
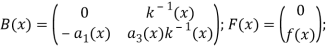
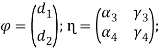
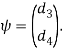
Литература:
- Олимов М, Жакбаров О. О., Ирискулов Ф. С. Алгоритм решения прикладных задач для обыкновенных дифференциальных уравнений четвертого порядка с методом дифференциальной прогонки «Молодой ученый» Ежемесячный научный журнал № 6(86) / 2015 г. часть 2.
- М. Олимов, Исмонова К., Каримов П., Исмоилов Ш. Математические пакеты прикладных программ. Учебное пособие. Типография «Тафаккур бўстони» Ташкент. 2015.
- М. Олимов, П. Каримов, Ш. Исмоилов. «К решению краевых задач пространственных стержней при переменных упруго-пластических нагружённый с учетом разгрузки». Научно-технический журнал. Ферганский политехнический институт. 2014. № 4.
- Олимов М., Ирискулов С., К. Исманова, А. Имомов. «Численные методы и алгоритмы». Учебное пособие. «Наманган». 2013.
