В настоящей статье рассматриваются определения формы и положения кривых 2-го порядка на плоскости и в пространстве, которые применяются для задания этих кривых и для определения положения плоскостей пересекающих поверхностей 2-го порядка по заданному коническому сечению.
Ключевые слова: прикладная геометрия, инженерная графика, графические дисциплины, кривые 2-го порядка, эллипс, гипербола, парабола, окружность, параметры, положения, формы, параметрическая мощность, центр
Многие годы в Ташкентском государственном педагогическом университете Республики Узбекистан подготавливаются магистры по специальности — 5А110802 — Инженерная графика и теория дизайна. В связи с этим в ТГПУ имени Низами как головной педагогический университет систематически совершенствуются типовые учебные и тематические планы по дисциплине «Прикладная геометрия» с новыми требованиями. При этом особенно уделяются внимание методам исследования кривых линии и поверхностей, которые часто встречаются на различных отраслях производства, как в машиностроении, так и в сооружениях строительства. Как известно, пространство заполнено множеством геометрических фигур для выделения из них определенных фигур требуется некоторые дополнительные условия. Например, определение параметров положения и формы геометрических фигур отвечающим наперед заданным условиям. Образование и построение кривых линии 2-го порядка часто встречаются в учебном процессе для построения линии пересечения кривых поверхностей 2-го порядка с плоскостью и между собой. Поэтому вопрос определения параметров положения и формы кривых линии 2-го порядка имеют особое место для преподавания графических дисциплин.
Параметры, определяющие положения кривых 2-го порядка называем параметрами положения кривых 2-го порядка. Параметры, определяющие вид (форму) кривых 2-го порядка, называются параметрами формы этих кривых.
В настоящей статье рассматривается один из способов определения параметров положения и формы кривых линии 2-го порядка, как на плоскости, так и в пространстве.
- Параметры формы и положения окружности.
1.1. Как известно, форма произвольной окружности определяется ее радиусом R, который является параметром формы окружности. Поэтому каждому определенному значению R, соответствует определенная форма окружности на плоскости и в пространстве. Следовательно, радиус окружностей на полоскости и в пространстве — одно параметрическое множеств, мощность которого равняется ∞1.
1.2. Параметры положение произвольной окружности на плоскости определяется заданием положения ее центром, который определяется двумя параметрами (рис. 1). Поэтому число параметров положения окружностей на плоскости будет равно двум, мощность этого множества равна-∞2. Следовательно, произвольную окружность на плоскости можно определить тремя параметрами: один — параметр формы (R), два — параметры положения (центр). Совокупность окружностей на плоскости является трехпараметрическое множество, мощность которого запишется ∞3.
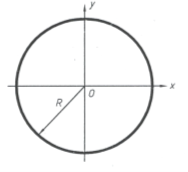
Рис. 1.
1.3. Параметры положение окружности в пространстве определяется заданием положения ее плоскости, который в пространстве зависит от трех параметров (рис. 2). Мощность множества плоскостей в пространстве равно — ∞3. Поэтому произвольную окружность в пространстве можно определить шестью параметрами, один параметр формы, пять параметров положения. Совокупность окружностей в пространстве шести параметрическое множество, мощность которого равна ∞6.
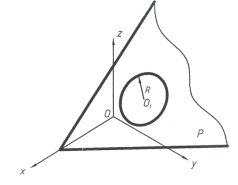
Рис. 2.
-
Параметры формы и положение параболы.
- Параметры формы параболы на плоскости и в пространстве определяется фокальным параметром — р. Следовательно, параметром формы параболы на плоскости и в пространстве однопараметрическое множество мощность которого будет ∞1.
![]() 2.1. Параметры положение произвольной параболы на плоскости можно определить заданием её вершины (или фокуса) и направлением оси параболы (рис. 3). Задание вершины параболы (точка) на плоскости определяется двумя параметрами, заданием направления оси параболы определяет еще один параметр. Следовательно, число параметров положения произвольной параболы на плоскости равно трем. Совокупность парабол на плоскости четырех параметрическое множество, мощность которого равна ∞4 (один — параметр формы. Три — параметры положения).
2.1. Параметры положение произвольной параболы на плоскости можно определить заданием её вершины (или фокуса) и направлением оси параболы (рис. 3). Задание вершины параболы (точка) на плоскости определяется двумя параметрами, заданием направления оси параболы определяет еще один параметр. Следовательно, число параметров положения произвольной параболы на плоскости равно трем. Совокупность парабол на плоскости четырех параметрическое множество, мощность которого равна ∞4 (один — параметр формы. Три — параметры положения).
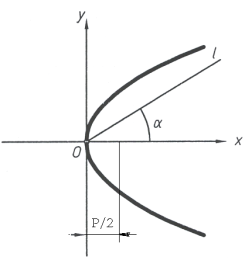
Рис. 3.
2.2. Параметры положение произвольной параболы в пространстве определяется заданием положения ее плоскости (рис. 4), который зависит от трех параметров мощность этого множества равна — ∞3. Следовательно, положение и форма произвольной параболы в пространстве можно определяться семью параметрами — ∞7 из них один — параметр формы, шесть — параметры положения. Совокупность всех парабол в пространстве — семи параметрическое множество, мощность которой запишится ∞7.
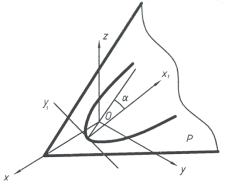
Рис. 4.
- Параметры формы и положения эллипса или гиперболы.
Известно, что из кривых второго порядка эллипс и гиперболы относятся к группе центральных кривых. Они имеют центр (точка) и главные оси, которые определят формы этих кривых. Поэтому определение параметров формы и положения эллипса и гиперболы будим рассматривать аналогично.
3.1. Форма эллипса и гиперболы на плоскости и в пространстве определяется заданием их главных осей, которые равны 2а и 2в (рис. 5). Поэтому величины осей этих кривых 2-го порядка являются параметрами формы кривых. Следовательно, число параметров, определяющих форму эллипса или гиперболы, равно двум мощность этого множества равна — ∞2.
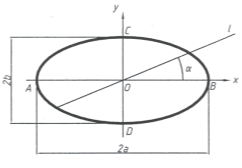
Рис. 5.
![]() 3.2. Параметры положение эллипса или гиперболы на плоскости можно определеить заданием его центра (точки) и направлением одной из осей (прямой). Так как вторая ось всегда перпендикулярна к первой. Таким образом, число параметров, определяющих положение эллипса или гиперболы на плоскости, равно трем. Совокупность эллипсов или гипербол на плоскости, пяти параметрическое множество (два — параметры формы, три — параметры положения на плоскости), мощность которого будет ∞5.
3.2. Параметры положение эллипса или гиперболы на плоскости можно определеить заданием его центра (точки) и направлением одной из осей (прямой). Так как вторая ось всегда перпендикулярна к первой. Таким образом, число параметров, определяющих положение эллипса или гиперболы на плоскости, равно трем. Совокупность эллипсов или гипербол на плоскости, пяти параметрическое множество (два — параметры формы, три — параметры положения на плоскости), мощность которого будет ∞5.
3.3. Параметры положение элипса или гиперболы в пространстве определяется заданием положения их плоскостей (рис. 6), который зависит от трех параметров мощность этого множества равна — ∞3. Так как в плоскости эллипса или гипербол определяется пятью параметрами ∞5, следовательно, совокупность эллипсов или гипербол в пространстве восьми параметрическое множество (из них два — параметры формы, шесть параметры положения), мощность которого будет равна ∞8.
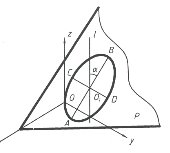
Рис. 6.
Выше приведенные соображения можно использовать для задания кривых 2-го порядка и для определения положения плоскостей пересекающих поверхности 2-го порядка по заданному коническому сечению.
Необходимо отметить, что изучая способы образования и задания некоторых других кривых более высокого порядка, можно определить число параметров формы и положение этих кривых.
Выше приведенные сведения для определения количество параметров формы и положения кривых 2-го порядка как на плоскости и в пространстве можно определить по таблице № 1.
Таблица 1
|
Виды кривых 2-го порядка |
Параметры формы |
Параметры положения |
||
|
На плоскости |
На пространстве |
Итог |
||
|
Окружность |
1 (R) |
2 |
3 |
6 |
|
Парабола |
1 (р) |
3 |
3 |
7 |
|
Эллипс |
2 (2а,2в) |
3 |
3 |
8 |
|
Гипербола |
2 (2а,2в) |
3 |
3 |
8 |
Литература:
- Нартова Л. Г., Тевлин А. М. «Курс начертательной геометрии» с алгоритмами ЭВМ. Москва, изд-во «МАИ», 1994.
- Мурадов Ш. К. Аналитико-графические методы решения обратных метрических задач и их применение в инженерной практике. Ташкент, изд-во «Фан», 1986.







