В настоящей статье рассматривается методика использования нового механизма для построения аксонометрических проекций.
Ключевые слова: аксонометрия, диметрия, изометрия, окружность, овал, эллипс, параметры, центр, положения, гипотенуза, ромб
На изображении куба в изометрической проекции (рис. 1) видно, что в одинаковых ромбах вписаны эллипсы. Данные эллипсы заменяются обычно овалами, построенными с помощью дуг окружностей из четырех центров. Соотношение осей овалов при этом берут 0,58:1.
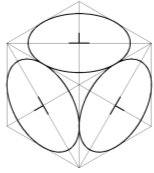
Рис. 1.
Для того чтобы найти численное значение размеров дуг этих овалов, можно воспользоваться прибором (рис. 1, а). Прибор изготовлен в виде сплошного чертежного угольника с углами 45º, 45º и 90º на плоскости которого нанесены наклонные прямые-номограммы. Передвигая движок, перпендикулярный к одному из катетов, с помощью номограмм определяют соответствующие радиусы дуг окружностей, необходимых при построении овалов, которые вычерчивают вместо эллипсов, с тем чтобы упростить графические построения тел вращения в аксонометрических проекциях. Если в треугольнике ИОК (где одна из вершин обозначена буквой И-изометрия, а другая буквой О-центр овала) нанести на катете ИО (см.рис. 2, а) деления от 0 до 100 мм, а катет КО в точке И1 разделить на две части в отношении 3:4, то прямая ИИ1 будет геометрическим местом центров малых дуг овалов; прямая ИО — геометрическим местом центром овалов и одновременно центров больших дуг овалов; прямая ИК — геометрическим местом концов больших полуосей овалов.
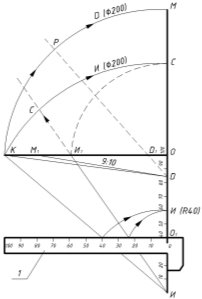
a)
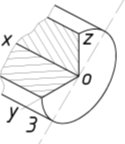
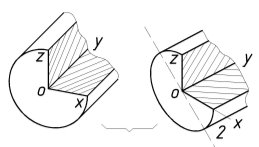
б)
Рис. 2.
На рис. 2, а показано построение четвертой части овала с центром в точке О. Большая полуось этого овала ОК-100 мм, малая полуось овала ОС1, равная ОИ1, находится построением. Точка С является точкой плавного перехода (сопряжения) контура малой дуга к большей дуге овала. По этим данным легко достроить циркулем полный овал. Рассмотрим построение овала с иными осями. По катету ОИ треугольника вверх и вниз передвигается движок 1. На его верхней кромке находится шкала с делениями от 0 до 100 мм. Ее нулевое деление всегда совпадает со шкалой катета ИО. На рис. 2, а движок расположен так, что его нулевая точка совпадает с делением 40 мм на шкале. Это значит, что большая полуось овала равна 40 мм. В этом случае Ги=0,42.40=17 мм; Rи=40–17+40=63 мм, где Ги и Rи-радиусы малой и большой дуг овала. Стрелками показано, в каком направлении проводят дуги окружностей для построения овала при заданном радиусе круга (40 мм). Сопрягаются дуги овала в точке с, лежащей на прямой ИИ1.
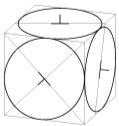
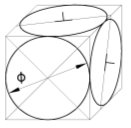
а) б)
Рис. 3.
На рис. 3, а, показан куб в прямоугольной диметрической проекции с вписанными окружностями в его видимые грани. Окружности в этой проекции также изображаются в виде эллипсов, замененных в данном случае четырехцентровыми овалами.
На фронтальной плоскости проекции соотношение осей овала, заменяющего эллипс, равно 9:10. Традиционное построение этого овала и нахождение радиусов двух попарно одинаковых дуг, проведенных из центров, расположенных симметрично на осях овала, показано на рис. 4.
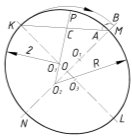
Рис. 4.
Построение выполняется следующим образом. Через центр О проводятся две взаимно перпендикулярные оси и дуга радиусом ОК=R, затем откладывается отрезок ОМ=0,9R R=
Наибольшие размеры сторон прямоугольного треугольника ДОК (при ОК = 100 мм) можно поместить внутри треугольника ИОК. Передвигай движок 1 в пределах катета ДО вверх и вниз, найдем размеры осей овала в пересечении с наклонными лучами ДК и ДМ1, а также радиусы дуг овалов при пересечении с лучом ДД1 (где ОД1 = 16 мм; ОД = 18 мм). Таким образом, прямоугольный равнобедренный треугольник ИОК с катетом, равным в 100 мм, и с нанесенными на нем наклонными лучами ИИ1, ДК; ДМ; ДД1 может быть использован для нахождения с помощью движка 1 всех параметров, необходимых для построения окружностей в изометрической и во фронтальной плоскости прямоугольной диметрической проекции.
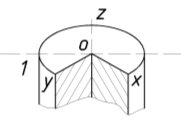
На обратной стороне треугольника ОИК (рис. 2, б) показаны основания цилиндров, соответственно параллельные берем плоскостям проекций Н, V и W в изометрической проекции. Каждый из цилиндров показан в разрезе с удалением четвертой части. Там же дан цилиндр с вырезом четвертой части в прямоугольной диметрический проекции, основание которого параллельно фронтальной плоскости проекции V. Если гипотенузу треугольника расположить горизонтально, то будет ясно видно, как располагаются оси эллипсов и цилиндров относительно осей и плоскостей проекций. На рис. 3, а и б показаны в плоскостях Н и W одинаковые овалы — изображения окружностей, вписанных в грани куба, — с соотношением осе 1:3. Если заданный диаметр окружности равен 100 мм, то большая ось овала будет равна 106 мм, а малая ось — 35 мм. Обычное построение этого овала и нахождение радиусов попарно-одинаковых дуг, проведенных из центров расположенных симметрично на осях овалов, показано на рис. 5.
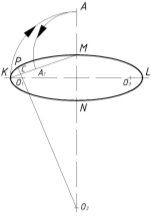
Рис. 5.
Вначале проводим две взаимно перпендикулярные оси (см. овал, расположенный в верхней грани куба на рис. 3, а) и отложим на них размеры осей овалов: ЛД = 1,06d и MN = 1/3 KL, где d — диаметр заданной окружности. Из центра О проведем дугу радиуса КО. Соединим точки К и М отрезком прямой и из точки М, как из центра, опишем дугу радиуса МА (МА=ОК-ОМ) до пересечения с прямой КМ в точке А1 т. е. МА1 = МА. Рисунок 5. Отрезок КА1 разделим пополам в точке С и проведем из нее перпендикуляр до пересечения с осями КL и MN в точках О1 и О2, которые принимаем за центры дуг окружностей радиусов r = О1К и R = О2Р. Точка Р, лежащая на линии центров О2О1, является точкой внутреннего касания (сопряжения) этих двух дуг окружностей. На большой и малой осях овала находим две точки лученных точек, как из центров, строим овал радиусами R и r. Из подобия прямоугольных треугольников КОМ и О1ОО2 можно записать: ОО2:ОО1= ОК:ОМ = R:R3=3, т. е. ОО2 втрое больше, чем ОО1. Для нахождения центра О1 надо полуось овала ОК разделить на пять равных частей, так как КО1= 1/5R=0,2R. Центр О2 находится на продолжении малой оси овала на расстоянии ОО2 = 3·ОО1= 3·4/5P=2,4P. На рис. 3, а и б показаны в плоскостях Н и W одинаковые овалы — изображение окружностей, вписанных в грани куба, с соотношением осей 1:3. В случае когда диаметр окружности равен 100 мм, оси овала будут равны 106 мм и 35 мм. При построении овала меньший радиус дуги rd = 0,1d; большие радиус дуги Rd = 1,36d (где rd и Rd — радиусы овала в диметрической проекции с соотношением осей 1:3). При d = 200 мм rd = (2 · 106): 5 = 21,2 мм; Rd = 3(106–21,2)+35,2 = 272 мм. Прибор, показанный на рис. 6, а, также служит для построения изображения в аксонометрических проекциях. Он состоит из сплошного прямоугольного треугольника с острыми углами в 30º и 60º. На лицевой плоскости треугольника нанесены лучи, проведенные из трех точек (d, И, Д) большого катета, равного 240 мм. Эти точки являются центрами больших дуг овалов. В треугольнике ИОК с лучами ИК и ИИ1 для изометрических проекций находится треугольник ДОК с лучами ДК, ДД1 и ДМ1 для диметрических проекций. По своим параметрам они полностью совпадают с данными на рис. 2, а. Зона треугольника используется для определения параметров прямоугольной и косоугольной диметрических проекций при построении овалов с соотношением осей 1:3. Прямая dК — геометрическое место концов больших полуосей овалов, прямая dd1 — геометрическое место центров малых радиусов rd, а также геометрическое место точек внутреннего касания малых и больших дуг овала; прямая dN — геометрическое место концов малых полуосей овалов. Установив движок 1 так, чтобы крайний луч dК пересекал его шкалу в делении 42 мм, получим в пересечении с лучом dd1 размер радиуса rd = 0,1·84 =8,4 мм, Rd = 1,36·8,4=114,2 мм. По этим размерам с помощью циркуля построена четвертая часть четырехцентрового овала. Остальную часть как симметрическую легко достроить по тем же размерам дуг окружностей.
Верхнее положение движка соответствует зоне треугольника ИОК.
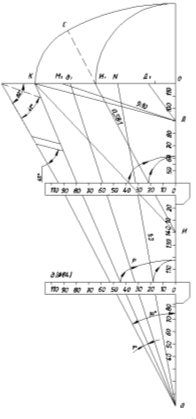
а)
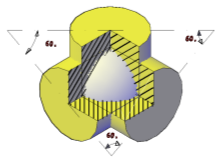
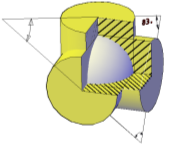
б)
Рис. 6.
Все параметры в этой зоне находятся аналогично тому, как это делалось на рис. 6, а. На оборотной стороне треугольника показаны части цилиндров с вырезом четвертой части (рис. 6, б). Основания цилиндров — круги расположены параллельно плоскостям проекций Н, V и W: И — в изометрической проекции; Д — в диметрической проекции. Для удобства построения некоторых углов со стороны гипотенузы прямоугольного треугольника сделаны вырезы. С их помощью в аксонометрической проекции можно получить углы не только в 30º и 60º, но и 7, 41º и 45º. Описание чертежного прибора позволит изготовить его учащимся средних школ, с тем чтобы использовать на практических занятиях и в кружках по техническому черчению.
Литература:
- Ш. К. Мурадов и д. Курс начертательная геометрия.–Т., Иқтисод-молия, 2009.







