Статья посвящена проблеме отсутствующей информации в теории баз данных, а именно, концепции, позволяющей определить, имеет ли атрибут значение или его значение не определено. Эта концепция так и называется — «Концепция трехзначной логики». Именно на ней мы остановимся более подробно.
Ключевые слова: базы данных, трехзначная логика, отсутствующая информация
Для дальнейшего рассмотрения вопроса разберемся, что есть трехзначная логика. Рассмотрим пример. Цвет детали под номером D1 может быть неизвестен, поэтому упрощенно можно сказать, что её цвет «является неопределенным». В более широком смысле это выражение подразумевает следующее:
1) деталь существует,
2) эта деталь имеет цвет,
3) цвет детали не известен. Другими словами, можно сказать, что мы не знаем точного цвета детали, которое можно использовать в качестве значения для атрибута цвета детали COLOR в кортеже, который описывает рассматриваемую деталь. Значение этого атрибута помечается как неопределенное.
Для удобства можно неформально сказать, что атрибут COLOR «содержит неопределенное значение» или значение этого атрибута «равно NULL или UNK». На практике подобные выражения используются довольно часто, так как нередко возникают ситуации, когда какие-либо данные неизвестны (относительно рассматриваемой в примере детали это может быть цвет, вес, расположение и др.). Но следует четко понимать, что подобные выражения немного неточны, так как под NULL-значением (то есть UNK) имеется ввиду, что кортеж вообще не содержит никакого значения атрибута COLOR. Поэтому выражение «неопределенное значение» или «значение UNK» часто использовать не рекомендуется.
При сравнении любых скалярных значений, в которых какой-либо из операндов не определен, вместо значения true (истина) или false (ложь) будет получено логическое значение unknown (не известно). Именно поэтому приходится оперировать тремя логическими значениями — true, false и unk (производная от unknown). Значение unk, в данном случае, и является «третьим логическим значением».
Ниже приведены таблицы истинности для операторов AND (рис. 1), OR (рис. 2) и NOT (рис. 3) в трехзначной логике (t-true, f-false, u-unk).
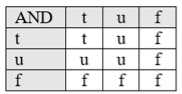
Рис. 1. Оператор AND
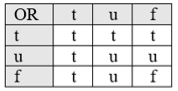
Рис. 2. Оператор OR
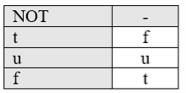
Рис. 3. Оператор NOT
Предположим, что A=1, B=2 и C — это величина UNK. Тогда показанные ниже выражения будут иметь следующие результаты:
A > B AND B > C: false
A > B OR B > C: unk
A < B OR B < C: true
NOT (A = C): unk
Если говорить о трехзначной логике, то этих трех операторов недостаточно. Один из наиболее часто используемых операторов — MAYBE (возможно). Таблица истинности приведена на рис.4.
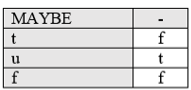
Рис. 4. Оператор MAYBE
Чтобы продемонстрировать необходимость этого оператора, рассмотрим запрос «Получить сведения о сотрудниках компании «Газпром» с годовой зарплатой не менее 40 тыс. долл., которые могут быть (но это точно не известно) инженерами-электриками и родились до 1 мая 1986 года». С помощью оператора MAYBE данный запрос можно достаточно кратко записать в следующем виде:
EMP WHERE MAYBE (JOB = 'MEngineer' AND DOB < DATE (1986–5-1)
AND SALARY < 40000.00)
Но следует понимать, что MAYBE — не единственный дополнительный логический параметр, который необходим в трехзначной логике. Существуют и другие весьма полезные операторы, которые применяются на практике.
В заключение, нужно указать, что значение UNK (неопределенное значение вида «значение неизвестно») и unk (логическое значение unknown) — это не одно и то же. В действительности, это является следствием того, что unk — это логическое значение, а UNK не является значением вообще.
Таким образом, в данной статье были рассмотрены основные проблемы отсутствующей информации в теории баз данных, а также концепция трехзначной логики, для которой были приведены соответствующие примеры и представлены таблицы.
Литература:
- Дейт К. Дж. Введение в системы баз данных, 8-е издание: Пер. с англ. — М.: Издательский дом «Вильяме», 2005. — 1328 с.: ил. — Парал. тит. англ.







