Метод прогнозирования течения сепсиса у детей раннего возраста



Патометрология, изучающая способы вычислительной диагностики и подходы математического прогнозирования, имеет ряд проблем, заключающихся в наличие области слабого распознавания и трудоёмкость разработки комплексных прогностических функций.

Мы разработали качественно новый способ распознавания и прогнозирования течения септического шока у детей раннего возраста с использованием термодинамических и синергетических функций, а также новый подход в прогнозировании течения неотложного состояния на примере септического шока с высокой прогностической ценностью, определённый нами как фазово-фрактальный анализ роста информационной энтропии.

Ключевые слова: сепсис, септический шок, шкалы, вычислительная диагностика, прогнозирование

Септический шок у детей, как причина смерти встречается в 4,5 % случаев вскрытий. У половины всех детей с сепсисом развивается шок. Смертность детей с септическим шоком достигает 45 % [3]. Факторами риска развития сепсиса являются ранний грудной возраст, мужской пол, недоношенность, неклассифицируемые иммунодефициты (35 % случаев сепсиса), транзиторная недостаточность иммунной системы (14 % случаев сепсиса). Среди умерших детей от септического шока несостоятельность иммунной системы была обнаружена в 57 % случаев [9].

Современное представление о септическом шоке основывается на предположении существования «цитокинового взрыва» — лавинообразного нарастания молекул активирующих иммунные клетки и приводящего к незавершённости фагоцитоза, увеличения уровня молекул определяющие интоксикацию организма, разрушение клеток и запускающие механизмы расстройств микроциркуляции.

Несмотря на успешное развитие способов интенсивной терапии, в том числе методов экстракорпоральной детоксикации смертность от септического шока в стадии декомпенсации составляет 47–50 % [3]. Важно различать развитие септического шока на начальном этапе развития, а также предположить его дальнейшее развитие для предотвращения трагических результатов. Разработка и внедрение подхода способного прогнозировать течение и исход септического шока в ранние сроки его развития сможет снизить смертность детей от этого неотложного состояния. Применяемые в медицине методы прогнозирования, основанные на разработке математических моделей, имеют прогностическую точность, не превышающую 90 % в распознавании сроков и выраженности эпизодов критических состояний. Это связано с трудностью получения максимальной модели прогнозирования, охватывающей цельный патологический процесс. Удаётся лишь получить модели отдельных подпроцессов. При увеличении количества диагностических тестов прогнозной шкалы уменьшается точность прогнозирования.

Исходя из этих положений, мы задались целью разработать подход в патометрологии позволяющий управлять этой ситуацией. Для этого мы изучили возможность применения математического аппарата термодинамики — области теоретической физики изучающую закономерности энергообмена систем, а также синергетики — область физико-математики изучающей проблемы устойчивости систем.

Материалы иметоды.

Для применения подходов термодинамики и синергетики мы нашли способ формализации клинической информации, построив шкалы относительного типа, в виде феноменологического ряда событий, то есть каждая градация шкалы является самостоятельным событием в цепи последовательного ряда развития, начиная с нормального состояния. Также мы нашли способ измерения клинической информации, вычисляя информационную энтропию — меру неустойчивости системы, применив для этого формулу Больцмана [2]:

S = k Ln W

Где S — значение энтропии, k — термодинамический коэффициент, равный 1,34; W — статистический вес макросостояния системы.

Каждая градация в последовательном ряде событий обладает статистическим весом, равному номеру градации и, следовательно, обладает энтропией. Чем больше статистический вес, тем выше значение энтропии. Так как энтропия сопряжённых систем обладает аддитивностью [2], то мы можем суммировать значения энтропии всех шкал и получить энтропию всей диагностической системы (Z).

Используя этот подход, мы разработали термодинамическую шкалу, которая была испытана в отделениях реанимации и интенсивной терапии трёх детских больниц на 52 детях с верифицированным септическим шоком и 159 детях с сепсисом, у которых не развился шок в когортном проспективном исследовании.

Дальнейшим этапом исследования была разработка способа прогнозирования неотложного состояния у детей. Решение мы нашли, применив метод Б. Мандельброта [2, 5, 6], для значений энтропии клинической информации полученных из шкалы. Для использования этого метода, необходимо было доказать, что течение неотложного состояния обладает фрактальностью — свойство системы развиваться по определённой закономерности, которой обладают большинство природных объектов [7, 8].

Процедура анализа начинается с выбора градации в шкалах 24 диагностических тестов. Затем значения энтропии каждой шкалы суммируется, и мы узнаём энтропию всей диагностической системы. Уже на этом этапе мы можем установить степень угрозы исследуемого неотложного состояния. Затем полученное значение мы переводим в относительную форму по формуле:

Z = 1 — (S_max — S_fakt) / S_max

Где Z — значение относительной энтропии, S_{max —} максимальная энтропия диагностической таблицы, S_fakt — фактическая энтропия по диагностической таблице.

На втором этапе, мы в динамическом исследовании по двум и более значениям относительной энтропии с помощью формулы Мандельброта узнаём прогноз роста энтропии:

Z_n+1 = Z₀ + Z_n + Z₀² + 2Z₀Z_n — Z_n²

Где Z_{0 —} значение относительной энтропии при первом измерении, Z_{n —} значение относительной энтропии при измерении через принятый интервал времени (например 30 минут), Z_{n+1 —} прогнозируемое значение относительной энтропии через принятый интервал времени.

Для определения степени стабильности состояния пациента и наличие резерва времени имеет значение продукции энтропии:

Z = Z_{n+1 —} Z_n

Представленный способ математического прогнозирования течения неотложного состояния предлагается определить как фазово-фрактальный метод.

Наблюдение проводилось на 52 детях в возрасте от 1 месяца до 3 лет в отделениях реанимации и интенсивной терапии детских больниц. Также было проведено наблюдение за 159 детьми с наличием гнойных очагов мягких тканей и сепсисом без развития шока.

Результаты иобсуждение.

Анализ информативности диагностических тестов по Вальду выявил, что ценностью для распознавания септического шока у детей и последующего использования их в показателей в прогностической модели имеют 21 из них (таблица).

Таблица 1

Диагностическая таблица для распознавания и прогнозирования течения септического шока

Баллы / Тест	0	1,0	1,4	2,0	2,2	2,4	2,6
Данные первичной и вторичной АВСД оценки
Оценка дыхания	Нормального объёма и звучания	Увеличенного объёма	Звучное дыхание	Патологическое	Апноэ	-	-
Оценка кровообращения	Пульс нормальный	Тахикардия	Отсутствие пульса на периферической артерии	Отсутствие пульса на центральной артерии	-	-	-
Оценка сознания	Вербальная реакция адекватная	Возбуждение	Сонливый при МЗ*	Сонливый без МЗ*	Кома при МЗ*	Кома без МЗ *	-
Мышечный тонус	Нормальный	Повышенный	Тремор	Приступ локализованный судорог	Приступ генерализованных судорог	Серия судорог	Судорожный статус
Цианоз	Нет	Периоральный	Акроцианоз	Разлитой с эффектом от 100 % КИ**	Разлитой без эффектом от 100 % КИ**	-	-
Тактильная оценка кожи конечностей	Нормальной сухости и теплоты	Влажные холодные	Сухая горячая	Холодные конечности	-	-	—
Ретракция	Нет	Крылья носа	Надключичные ямки	Межреберья	Подреберья	Кивательные движения	-
Частота дыхания	До 60/50/40***	Более 60/50/40***	Менее 10	Нет	-	-	-
Частота сердечных сокращений	До 120 в покое	121–160	160–180	181–200	Более 200	Менее 60	Нет
Температура тела	36,5–37	37,1–38	38,1–39,5	39,6–40,5	40,6 и выше	36,4 и менее	-
Диурез	Регулярный	Обильный, частый	Редкий	Не мочился	-	-	-
Тахиаритмия	Нет	Трепетание предсердий	Фибрилляция предсердий	Желудочковая тахикардия	Суправентрикулярная тахикардия	-	-
АВ блок	Нет	1 степени	2 степени тип 1	2 степени тип 2	3 степени	Ритм соединения	Идеовентрикулярный ритм
Тест на выявление сепсиса и септического шока
Прокальцитонин плазмы крови	< 0,05 нг/мл	0,05–0,5 нг/мл	0,5–2 нг/мл	2–10 нг/мл	> 10 нг/мл	-	-
Лейкоциты крови	4000–12000	> 12000	< 4000	-	-	-	-
РаСО2	> 4,3 кРа	< 4,3 кРа		-	-	-	-
Калий сыворотки крови	3–4,9 ммоль/л	< 3 ммоль/л	> 5 моль/л	-	-	-	-
Натрий сыворотки крови	125–144 ммоль/л	< 125 или > 144 ммоль/л		-	-	-	-
НСО3 сыворотки крови	15–19 ммоль/л	> 20 моль/л	< 15 ммоль/л	-	-	-	-
Билирубин сыворотки крови	68,4–102.5 моль/л	> 102,6 моль/л	< 68,4 ммоль/л	-	-	-	-
Суточный диурез	< 500 мл/сут	500–900 мл/сут	> 1000 мл/сут	-	-	-	-

Примечание: * — МЗ — медикаментозное загружение; ** — КИ — кислородная ингаляция; *** — 60/50/40–60 — частота дыхания у ребёнка в возрасте до 1 месяца, 50 — до 1 года, 40 — старше 1 года

Графики прогнозной функции и данных фактического нарастания энтропии демонстрируют наличие пиков их возрастания. При достижении показателя энтропии 0,2 у детей начиналось состояния гемодинамической нестабильности. При достижении показателя 0,3 развивался «теплый» (компенсированный-субкомпенсированный) шок. Показатель 0,4 и выше встречался у всех детей с признаками «холодного» (декомпенсированного) шока (рисунок 1).

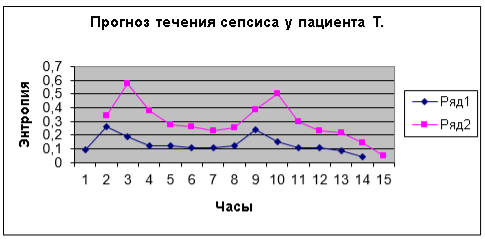
Рис. 1. Ряд 1 – Фактический рост энтропии; ряд 2 — Предсказанный рост энтропии по данным первых двух наблюдений

Данные прогноза с точностью до 60 минут указывали на сроки начала развития шока и скорости нарастания симптоматики. Однако предсказанные амплитуды нарастания энтропии отличались от фактических показателей, указывая на более угрожающие показатели. Дети, у которых не был распознан сепсис, имели в прогнозе и в катамнезе отсутствие пиков нарастание показателей энтропии.

Корреляционный анализ роста энтропии по Пирсону фактических пациентов с сепсисом с сопутствующей кардиомиопатией и значениями предсказанной функции показал её высокую эффективность в пределах 0,92–0,99 в разные сроки наблюдения. Специфичность прогнозной шкалы на этапе вычислительной диагностики составило 95 %, чувствительность шкалы составило 93 % при доверительном интервале 95 %.

Вывод. Графики прогнозных функций предсказывают с точностью до 2 часа +/- 23 мин сроки наступления шока. Предложенный метод прогнозирования роста энтропии клинической информации обладает высокой прогностической ценностью.

Литература:

1. Брейеуэлл Р. Н. В мире науки — 1986, № 8, с. 48.
2. Волькенштейн М. В. Биофизика. — М.: Наука, 1988 с. 301–312.
3. Недашковский Э. В., Киров М. Ю., Егорина Е. М., Совершаев М. А., Середкина Н. Е., Евгенов О. В. SAPS II — опыт применения для оценки тяжести состояния больных с септическим шоком. Вестник интенсивной терапии, 1999, № 2. с. 3–7.
4. Кратчфилд Дж., Фармер Дж. Д., Паккард Н. Х., Шоу Р. С. Хаос / В мире науки. — 1987, № 3. с. 16–28.
5. Сандер Л. М. Фрактальный рост / В мире науки. — 1987, С. 62–69.
6. Bracewell R. N. The Hartley transform. Oxford University Press, 1986.
7. Mandelbrot B. B. The fractal geometry of nature. WH Freeman and Company, 1982.
8. Packard N. H., Crutchfield J. P., Farmer G. D., Show R. S. Geometry from a time series / Physical Review Letters. 1980, Vol. 45, № 9, p. 712–716.
9. J. Pugin, M. Meisner, A. Leon, D. Gendrel, A. Lopez Gude for the clinical use of procalcitonin in diagnostis fnd monitoring of sepsis. BRAHMS, 7^th edition, 2008.