Данная работа является продолжением статьи [1], в которой проекции векторов ![]() и
и ![]() были получены на выходе апериодических звеньев. В этой статье проекции векторов выведены на основе интегрирующих звеньев.
были получены на выходе апериодических звеньев. В этой статье проекции векторов выведены на основе интегрирующих звеньев.
В работе [1] было получено уравнение (13):
![]()
Потокосцепление ψrx по оси (+1) определится в следующей форме:
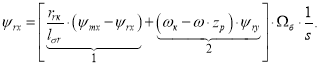
Структурная схема для определения ψrx приведена на рис. 1.
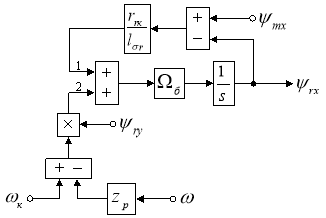
Рис. 1. Структурная схема для определения потокосцепления ψrx
Для определения ψmx приведем уравнение (14) из работы [1]:
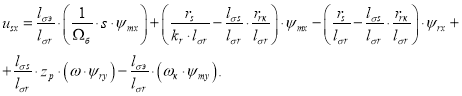
Перенесем слагаемое
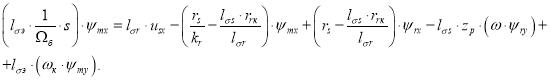
Обозначим ![]() и
и ![]()
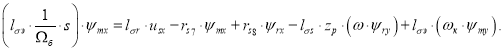
Тогда ψmx определится в следующей форме:
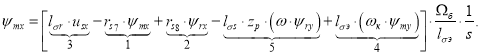
Структурная схема для определения ψmx представлена на рис. 2.
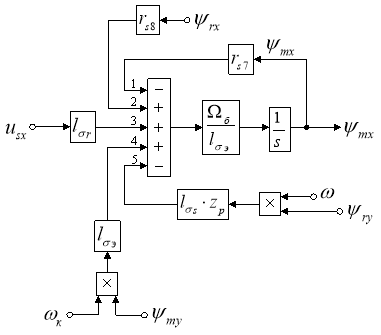
Рис. 2. Структурная схема для определения ψmx
Аналогично, определим ψry и ψmy по оси (+j).
Выразим ψry из уравнения (15), полученного в работе [1]:
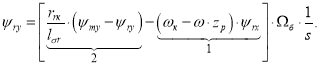
Структурная схема для определения ψry приведена на рис. 3.
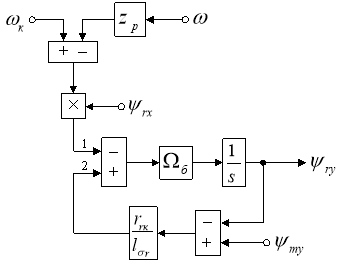
Рис. 3. Структурная схема для определения ψry
Для определения ψmy приведем уравнение (16) из работы [1]:
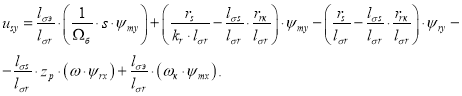
Перенесем слагаемое ![]() в левую часть и умножим обе части уравнения на
в левую часть и умножим обе части уравнения на ![]() :
:
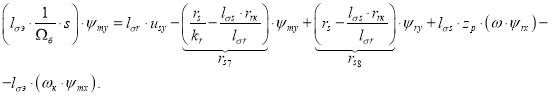
Отсюда потокосцепление ψmy определится в следующей форме:
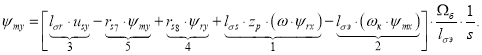
Структурная схема для определения ψmy дана на рис. 4.
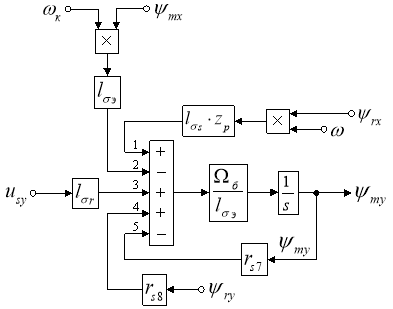
Рис. 4. Структурная схема для определения ψmy
На рис. 5 представлена структурная схема для реализации уравнения электромагнитного момента:
![]()
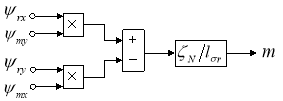
Рис. 5. Математическая модель определения электромагнитного момента m
Из уравнения движения выразим механическую угловую скорость вращения вала двигателя (рис. 6):
![]()
![]()
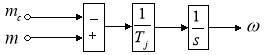
Рис. 6. Математическая модель уравнения движения
Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными ψr – ψm на выходе интегрирующих звеньев приведена на рис. 7. Параметры асинхронного двигателя рассмотрены в работах [2] и [3].
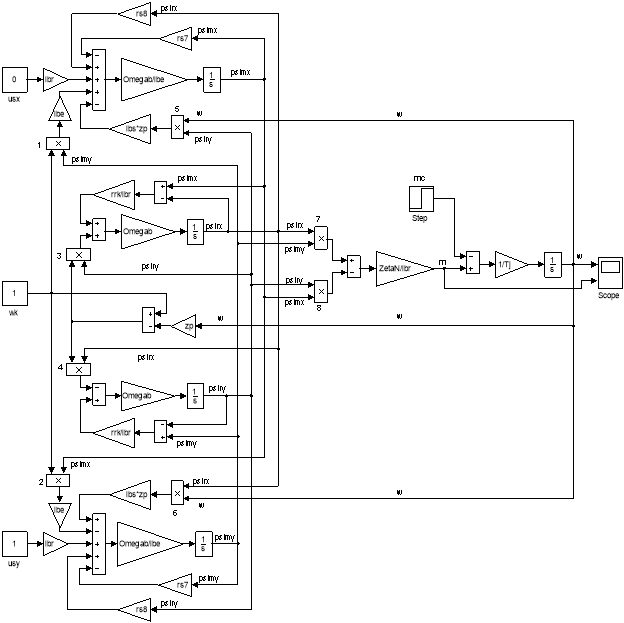
Рис. 7. Математическая модель асинхронного двигателя с переменными ψr – ψm на выходе интегрирующих звеньев
Расчет параметров производим в Script:
|
PN=320000; UsN=380; IsN=324; fN=50; Omega0N=104.7; OmegaN=102.83; nN=0.944; cos_phiN=0.92; zp=3; Rs=0.0178; Xs=0.118; Rr=0.0194; Xr=0.123; Xm=4.552; |
J=28; Ub=sqrt(2)*UsN; Ib=sqrt(2)*IsN; OmegasN=2*pi*fN; Omegab=OmegasN; Omegarb=Omegab/zp; Zb=Ub/Ib; Psib=Ub/Omegab; Lb=Psib/Ib; kd=1.0084; Mb=kd*PN/OmegaN; Pb=Mb*Omegarb; rs=Rs/Zb; lbs=Xs/Zb; |
rr=Rr/Zb; lbr=Xr/Zb; lm=Xm/Zb; Tj=J*Omegarb/Mb; betaN=(Omega0N-OmegaN)/Omega0N; SsN=3*UsN*IsN; ZetaN=SsN/Pb; ks=lm/(lm+lbs); kr=lm/(lm+lbr); lbe=lbs+lbr+lbs*lbr*lm^(-1); roN=0.9962; rrk=roN*betaN; rs7=rs/kr-lbs*rrk/lbr; rs8=rs-lbs*rrk/lbr; |
Результаты моделирования асинхронного двигателя представлены на рис. 8.
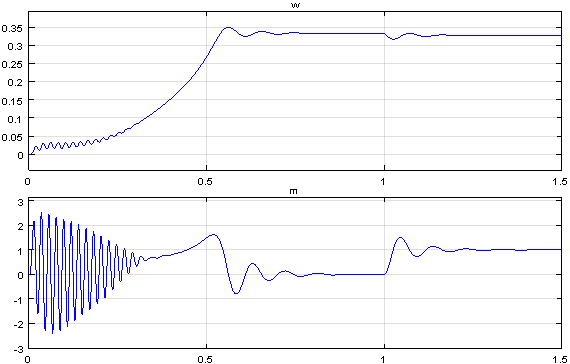
Рис. 8. Графики скорости и момента
Литература:
- Емельянов А.А., Бесклеткин В.В., Забузов Е.И., Волков Е.Н., Попов С.Ю., Соснин А.С., Вандышев Д.М., Найф А.В., Воротилкин Е.А., Камолов И.И. Математическая модель асинхронного двигателя с переменными ψr – ψm на выходе апериодических звеньев в Simulink-Script // Молодой ученый. - 2017. - №10.
- Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. - 654 с.
- Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.







