Нам известно, что построение квадратурных формул, основанное на методах функционального анализа была начата в работах А.Сарда [1] и С. М. Никольского [2], для кубатурных формул С. Л. Соболева [3]. Работы многих авторов, например (см. [1–3]) священны квадратурные формулы в которых входят значения производных интегрируемых функций. Если известны не только значения функции ![]() в точках
в точках ![]() на
на ![]() , но и значения её производные некоторых порядков, то естественно, что при правильном использовании всех этих данных можно ожидать более точный результат, чем в случае в случае использования только значений функций [2].
, но и значения её производные некоторых порядков, то естественно, что при правильном использовании всех этих данных можно ожидать более точный результат, чем в случае в случае использования только значений функций [2].
В связи с этим рассмотрим квадратурную формулу типа Эрмита
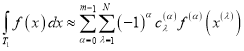 ,(1)
,(1)
с функционалом погрешности ![]() (2)
(2)
над пространством С. Л. Соболева ![]() . Где соответственно
. Где соответственно ![]() и
и ![]() являются произвольными коэффициентами и узлами квадратурной формулы (1),
являются произвольными коэффициентами и узлами квадратурной формулы (1), ![]() ,
, ![]() — одномерный тор, т. е. окружность длины равной единицы и
— одномерный тор, т. е. окружность длины равной единицы и ![]() — порядок производных,
— порядок производных, ![]() характеристическая функция
характеристическая функция![]() , и
, и ![]() — дельта функция Дирака.
— дельта функция Дирака.
Определение. Пространство ![]() — определяется как пространство функций заданных на одномерном торе
— определяется как пространство функций заданных на одномерном торе ![]() и имеющих все обобщённые производные порядка
и имеющих все обобщённые производные порядка ![]() суммируемые с квадратом в норме [3]
суммируемые с квадратом в норме [3]
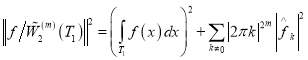 , (3)
, (3)
где ![]() — коэффициенты Фурье т. е.
— коэффициенты Фурье т. е. 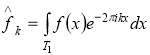 .
.
В работе [3] доказана следующая теорема.
Теорема 1. Квадрат нормы функционала погрешности (2) квадратурной формулы типа Эрмита вида (1) над пространством ![]() равен
равен
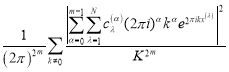 , (4)
, (4)
где ![]() — коэффициенты,
— коэффициенты, ![]() — узлы квадратурной формулы (1).
— узлы квадратурной формулы (1).
Отыскание минимума нормы функционала погрешности по ![]() и
и ![]() есть задача исследование функции на экстремум. Значения
есть задача исследование функции на экстремум. Значения ![]() и
и ![]() , реализующие этот минимум, определяют оптимальную квадратурную формулу.
, реализующие этот минимум, определяют оптимальную квадратурную формулу.
Основным результатом настоящей работы является
Теорема 2. Оптимальная квадратурная формула типа Эрмита вида (1) в периодическом пространстве ![]() при
при ![]() , имеет равноотстоящие узлы
, имеет равноотстоящие узлы ![]() ,
, ![]() и равные коэффициенты
и равные коэффициенты ![]() =
= ![]() = … =
= … = ![]() =
= ![]() и
и ![]() , которые выражаются формулой
, которые выражаются формулой
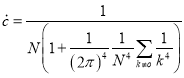 и
и ![]() . (5)
. (5)
Доказательство. Пусть в равенстве (4) ![]() , тогда
, тогда ![]() и в этом случае после некоторых преобразований над вторым слагаемым в равенстве (4) получаем
и в этом случае после некоторых преобразований над вторым слагаемым в равенстве (4) получаем
![]() =
=![]() +
+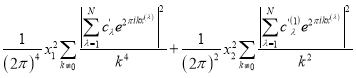 . (6)
. (6)
Используя результаты работы [9,10], из (6) получим
![]() =
=![]() +
+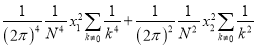 . (7)
. (7)
Здесь мы учитывали, что суммы 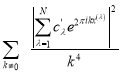 и
и 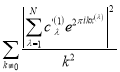
достигает своего наименьшего значения, равного соответственно
![]() и
и ![]() ,
,
когда узлы ![]() квадратурной формулы (1) равноотстоящие и все
квадратурной формулы (1) равноотстоящие и все
коэффициенты ![]() , также
, также ![]() равны между собой, т. е.
равны между собой, т. е.
![]() ,
, ![]() и
и ![]() . (8)
. (8)
Правую часть (7) будем рассматривать, как функцию от ![]() ,
,![]() и обозначим ее через
и обозначим ее через ![]() т. е.
т. е.
![]() =
=![]() +
+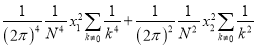 . (9)
. (9)
Тогда из необходимого условия экстремума из (7) получим систему уравнений с двумя неизвестными ![]() и
и ![]() .
.
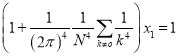 ,
, 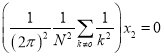 (10)
(10)
Решая систему (10) и введя некоторые преобразование, последовательно находим ![]() и
и ![]() , т. е.
, т. е. 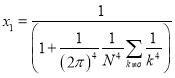 , и
, и ![]() . (11)
. (11)
Пусть ![]() и
и ![]() ,
, ![]() тогда имеем
тогда имеем ![]() и
и ![]() . Отсюда следует, что
. Отсюда следует, что
Подставляя (11) в (12) находим оптимальные коэффициенты квадратурных формул типа Эрмита вида (1), т. е.
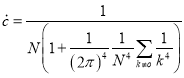 (13)
(13)
и ![]() , что и требовалось доказать.
, что и требовалось доказать.
Литература:
- Sard. A. Integral representations of remainders, Duke Math J. 1948. V15, 333–345
- Никольский С. М. К вопросу об оценках приближений квадратурными формулами успехи математических наук, 1950, Т.5, вып 2 (36), с. 165–177.
- Соболев С. Л. Введение в теорию кубатурных формул М.Наука 1974, 808с.







