В статье приводятся примеры использования компьютерных моделей электростатических полей точечных зарядов для формирования понятия электрического поля.
Ключевые слова: обучение физике, теория поля, визуализация, компьютерное моделирование, компьютерная модель, модель, электростатическое поле, силовые линии, эквипотенциальные линии, линии равного потенциала, электрический заряд
Кратко визуализацию можно охарактеризовать как мысленное представление некоторых образов. Каждый из нас занимается визуализацией, только зачастую этот процесс происходит неосознанно. Например, визуализация происходит, когда возникают образы при чтении книги. Человек не прилагает для этого специальных усилий, эти образы появляются сами собой. Однако бывает, что люди визуализируют и осознанно. Человек может представлять мысленно ту или иную ситуацию, например, предстоящее выступление с докладом на конференции.
Компьютерная визуализация предполагает визуальное представление результатов каких-либо исследований с помощью средств компьютерной графики [2]. Она помогает человеку переводить абстрактные образы в визуальные. Такое представление данных облегчает обработку информации и обмен ею. Наиболее важная особенность этой визуализации заключается в создании оптических образов объектов, которые нельзя увидеть. Многие физические эксперименты имеют цель, заключающуюся в том, что нужно сделать физические процессы или пространственные распределения видимыми. Например, к ним можно отнести эксперименты в камере Вильсона, подкрашивание ламинарных потоков жидкости, эксперименты в аэродинамической трубе и т. п.
Одной из целей изучения физики в школе является формирование у учащихся представлений о физической картине мира [5, с. 4; 6, с. 4]. Среди задач, решение которых обеспечивает достижение этой цели, можно выделить знакомство учащихся с методом научного познания и методами исследования объектов и явлений природы [5, с. 4]. Важным инструментом научного познания на современном этапе является компьютерное моделирование [4], поэтому учащиеся должны быть знакомы с ними понимать, как можно его использовать для познания окружающего мира. Продемонстрировать возможности компьютера при моделировании тех или иных физических объектов можно, рассматривая на уроках физики понятие электрического поля [1, с. 4–29; 3, с. 4–10; 6, с. 29].
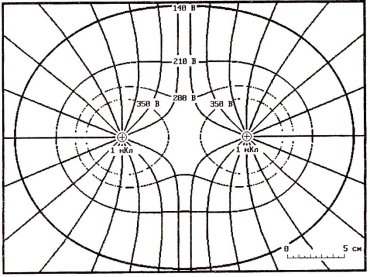
Рис. 1. Изображение линий равного потенциала и силовых линий поля двух одинаковых по величине точечных зарядов одного знака
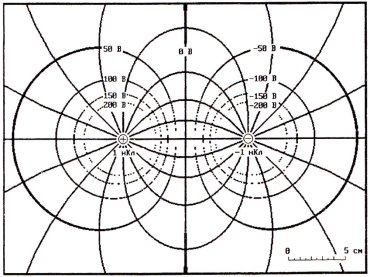
Рис. 2. Изображение линий равного потенциала и силовых линий поля двух одинаковых по величине точечных зарядов противоположных знаков
Графическое представление электростатического поля с помощью векторов напряженности, изображенных в различных точках поля, неудобно. Векторы накладываются друг на друга, при этом получается очень запутанная и непонятная для обучающихся картина. Считается, что более наглядным является метод, предложенный М. Фарадеем, который заключается в изображении электростатических полей с помощью силовых линий (линий напряженности). Эти линии не пересекаются, так как в каждой точке вектор напряженности имеет только одно направление. Кроме того, для изображения полей используются линии равного потенциала (или эквипотенциальные линии), то есть такие, в каждой точке которых электростатический потенциал имеет одно и то же значение. На рис. 1 показано поле двух точечных электрических зарядов, изображенное с помощью силовых и эквипотенциальных линий.
При обучении важно показать школьникам, чем отличаются поля двух одинаковых по модулю точечных электрических зарядов, если в одном случае имеем заряды одного знака (рис. 1), а в другом — разных знаков (рис. 2). Также с дидактической точки зрения важной является демонстрация, показывающая, как изменяется картина поля, если абсолютные величины зарядов изменяются (рис. 2 и 3).
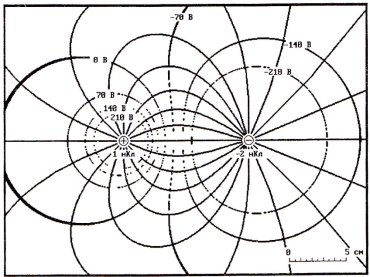
Рис. 3. Изображение линий равного потенциала и силовых линий поля двух разных по величине точечных зарядов противоположных знаков
Часто преподаватель ограничивается демонстрацией полей только двух зарядов, что является явно недостаточным. Необходимо показать учащимся, как выглядят и более сложные по конфигурации поля (рис. 4 и 5), созданные большим, чем два, количеством точечных зарядов.
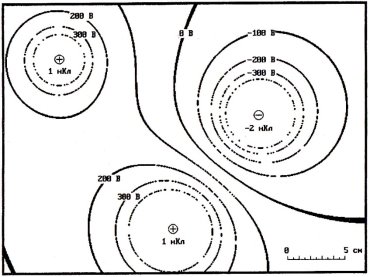
Рис. 4. Линии равного потенциала поля трех точечных зарядов
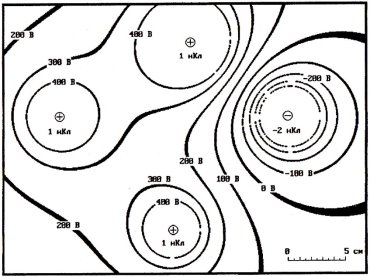
Рис. 5. Линии равного потенциала поля четырех точечных зарядов
Наглядное изображение поля в виде силовых линий дает представление о топологии поля. Наибольшей наглядностью при этом обладают двумерные поля или поля, обладающие аксиальной симметрией, для которых можно построить двумерные карты линий поля. Делать это «вручную» достаточно точно очень сложно. Картина получается очень приблизительной. В этом случае на помощь может прийти компьютер. Существует огромное количество пакетов программ, способных по заданным параметрам представить наглядную картину поля. Однако их недостатком является закрытость, или точнее, недоступность пользователю алгоритма визуализации поля. Бо́льшую ценность имеет обучение учащихся построению картины поля с помощью алгоритмических языков, когда применение алгоритма построения помогает понять теорию поля, математический аппарат которой довольно сложен и недоступен учащимся для понимания.
Например, вряд ли большинство школьников способны понять запись:
Однако они довольно легко способны понять геометрическую интерпретацию этого математического выражения: вектор напряженности электрического поля всегда направлен в сторону, противоположную наибыстрейшему возрастанию электрического потенциала поля. Это и может быть реализовано ими в алгоритме построения линий напряженности электрического поля. Иными словами, при построении линий поля последовательность действий будет следующая. Построение каждой линии начинается от места размещения точечного электрического заряда. При этом заранее определяется число направлений, в которых будет осуществляться построение линий (обычно сначала они равноудалены друг от друга). Выбирается шаг вдоль линии (длину прямолинейного отрезка). Из таких прямолинейных отрезков небольшой длины и будет состоять линия напряженности. Перемещаясь в заданном направлении, попадаем в точку, вокруг которой находится множество равноудаленных точек, в которых определяется значение электрического потенциала. Ясно, что эти точки размещены на окружности с радиусом, равным шагу вдоль линии. Определяются разности потенциалов точки в центре окружности и точек на ее дуге. Находится наибольшее значение разности. В результате осуществляется построение линии в противоположную сторону. Перемещаемся в следующую точку и повторяем все действия. Построение одной линии завершается тогда, когда линия достигает места размещения другого точечного заряда. Затем алгоритм применяется для построения следующей линии. Таким образом основы теории поля запоминаются и осознаются учащимися именно при составлении такой компьютерной программы.
Построение эквипотенциальных линий осуществляется проще. Нужно выбрать интервал, через который будут строиться такие линии, и отмечать точки, в которых потенциал одинаков. Однако, учитывая то, что экран компьютера дискретен, а расчет потенциала приблизителен, таких точек вообще может не быть. Поэтому строятся не линии, в каждой точке которых потенциал одинаков, а линии, в точках которых значения потенциала находятся в некотором заданном небольшом интервале. В связи с этим линии будут иметь неодинаковую толщину, так как в некоторых частях поля значения потенциала изменяются по мере продвижения по полю быстрее (рис. 4 и 5).
Рассмотренные в статье алгоритмы построения линий напряженности и равного потенциала не являются оптимальными в плане программирования и наиболее точно отражающими картину поля, они оптимальны в плане обучения. Строя с их помощью картину поля на экране компьютера, учащиеся знакомятся с элементами теории поля, изучить которые с помощью математического аппарата они пока не могут.
Литература:
- Голубева И. С. Физика 10: Электростатика: Рабочая тетрадь / И. С. Голубева, О. Е. Данилов, Р. В. Майер, А. В. Проказов; Под ред. В. В. Майера. — Глазов: ГГПИ, 1997. — 80 с.
- Данилов О. Е. Компьютерная визуализация учебной информации по физике / О. Е. Данилов // Школьная педагогика. — 2016. — № 2. — С. 26–30.
- Данилов О. Е. Физика 8: Электрические и магнитные явления: Рабочая тетрадь / О. Е. Данилов, Ю. В. Иванов, Т. Г. Мельм, Е. Г. Московкина; Под ред. В. В. Майера. — Глазов: ГГПИ, 1997. — 80 с.
- Данилов О. Е. Формирование умения проводить теоретическое исследование при изучении распределения физической величины в пространстве с помощью компьютерной модели / О. Е. Данилов // Дистанционное и виртуальное обучение. — 2013. — № 7. — С. 84–94.
- Примерные программы по учебным предметам. Физика. 7–9 классы. Естествознание. 5 класс: проект. — 2-е изд. — М.: Просвещение, 2010. — 80 с.
- Примерные программы по учебным предметам. Физика. 7–9 классы: проект. — М.: Просвещение, 2011. — 48 с.







