Обучение в военном вузе — сложный и многогранный процесс, на протяжении которого у курсантов закладываются основы профессиональных знаний.
Организация самостоятельной работы курсантов является одним из важнейших вопросов в условиях реализации компетентностной модели образования [1, с.4].
Особую категорию внеаудиторной самостоятельной работы курсантов представляет военно-научное общество (ВНО), включающее в себя углубленное изучение отдельных вопросов учебной программы, конструирование, моделирование, написание рефератов и сообщений, участие в научных конференциях и т. д. Творческая составляющая работы курсантов в ВНО должна активно формировать практические навыки, необходимые для профессиональной подготовки будущих военных специалистов.
Активная самостоятельная работа курсантов военного ВУЗа возможна, например, при организации учебно-познавательной деятельности, результатом которой станет создание проекта. Учебный проект — это интегративное дидактическое средство обучения, воспитания и развития, позволяющее сформировать ряд учебных компетенций.
В окружающем нас мире самыми распространенными процессами являются колебательные. Это и биологические ритмы — колебания, которые присущи всем живым организмам, и колебания ионов и атомов в твердых телах, и вращательное движение космических объектов, представляющих суперпозицию двух взаимно перпендикулярных колебаний, и колебательное движение самолетов при посадке в сложных метеорологических условиях. Изучение физики колебаний базируется на применении абстрактной модели.
Согласно работе [2, с. 9], модель — это мысленно представленная или реально существующая система, находящаяся в определенных отношениях с другой системой, называемой объектом или оригиналом. Объектом может быть физический процесс, явление, тело.
Целостная физическая модель, имея границы применения, должна позволить установить сходство модели и оригинала по ряду признаков, разрешить заменять реальный объект физической моделью, экстраполировать полученную информацию при изучении модели на реальный физический объект. Например, модель «математический маятник» используется при изучении гармонических колебаний тела в однородном поле тяготения.
Темой нашего проекта стали «Свободные незатухающие гармонические колебания».
Описание нашего проекта:
1) по характеру преобладающей деятельности: практико-ориентированный;
2) по цели: решение практической задачи изучения гармонического колебания на примере математического маятника;
3) по типу деятельности обучающегося: практическая деятельность в определенной учебно-предметной области;
4) по предметно-содержательной области: монопроект по физике;
5) по числу участников: коллективный;
6) по продолжительности: длинный (в течение семестра в часы самостоятельной работы в рамках работы в секции ВНО кафедры физики);
7) по проектному продукту: действующая модель для наглядной демонстрации гармонических колебаний;
8) по формируемым компетенциям: деятельностная, мыслительная.
При изучении законов колебаний математического маятника следует показать, что: 1) период и частота колебаний не зависят от массы и амплитуды колебаний; 2) период колебаний прямо пропорционален квадратному корню из длины математического маятника; 3) при небольших затуханиях выполняется закон сохранений механической энергии; 4) осцилляторы будут двигаться в одном направлении при равенстве их фаз.
Изучение гармонических колебаний начнем с рассмотрения поведения математических маятников при их центральном ударе в случае плоского движения.
Чтобы колебания происходили в одной плоскости и удары были центральными, лучше подвесить каждый шарик на двух нитях одинаковой длины, расположенных под небольшим углом друг к другу на прочно укрепленной раме.
Наблюдаемые колебания будут гармоническими только при соблюдении двух условий: 1) нерастяжимость нитей подвеса; 2) малый угол отклонения от положения равновесия за счет внесенной энергии в замкнутую систему. Трением нитей о раму будем пренебрегать.
Проанализируем случай центрального удара трех математических маятников, расположенных на одной прямой. Первому маятнику, масса которого
, сообщается энергия, его скорость становится равной 
. Он абсолютно упруго соударяется со вторым покоящимся маятником с массой 
. Затем второй маятник — с третьим массой
, который вначале находится в состоянии покоя. Если массы маятников неодинаковы, то следует определить массу второго маятника, чтобы скорость третьего была максимальной.
Исследуем столкновение первого и второго маятников на основе законов сохранения импульса и энергии:
где 
, 
скорости первого и второго маятников после центрального удара.
Решение этой системы дает формулы по определению искомых скоростей:
Аналогичный расчет для второго соударения приводит к выражению по определению скорости третьего маятника:
Проанализируем полученную формулу.
Вследствие того, что 
= const, максимум дроби будет при минимуме знаменателя, в котором массы первого и третьего маятников являются постоянными величинами.
Перепишем часть знаменателя выражения (3) и преобразуем его математически:
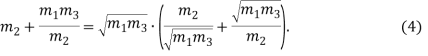
Для поиска экстремума воспользуемся математическим соотношением:
, если 
. В нашем случае искомый максимум скорости достигается, если 
.
Если же массы маятников одинаковы, то согласно законам сохранения импульса и энергии для замкнутой системы начальная скорость первого и последнего маятников в цепочке будут равны, т. е. 
. Максимальная кинетическая энергия первого маятника превращается в максимальную потенциальную энергию последнего. Крайний маятник свободно движется, поднимается на высоту h, останавливается и начинает движение вниз. Все повторяется.
Второй задачей, которую нужно было экспериментально решить: определить момент времени начала плоского движения в одном направлении соседних маятников с разным периодом колебаний.
Маятники, совершающие колебания по гармоническим законам c равной амплитудой 
будут двигаться в одном направлении только тогда, когда их фазы будут одинаковыми:
.
Следовательно, момент времени начала движения соседних маятников разной длины в одном направлении будет определяться выражением:
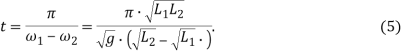
На раме подвесили 15 маятников одинаковой массы. Длины нитей отличались приблизительно на 1 см. Мы рассчитали их периоды и собственные частоты колебаний, а также моменты времени начала движения соседних маятников разной длины в одном направлении. Данные представлены в таблице.
Таблица
Параметры пятнадцати математических маятников
|
№ |
L, см |
t, с |
T, c |
n |
t, c |
|
1 |
21 |
60 |
0,923 |
65 |
|
|
2 |
22 |
60 |
0,942 |
64 |
19,5 |
|
3 |
23 |
60 |
1,140 |
63 |
20,7 |
|
… |
… |
… |
… |
… |
|
|
14 |
33 |
60 |
1,158 |
52 |
40,6 |
|
15 |
34 |
60 |
1,176 |
51 |
37,2 |
Движения маятников отличаются периодом, собственной частотой и фазой колебаний. Из таблицы видно, что самый короткий математический маятник делает 65 колебаний в минуту, каждый следующий совершает на одно колебаний больше, чем предыдущий, а самый длинный — 51 колебание.
Можно наглядно продемонстрировать изменение времени движения соседних математических маятников, частоты колебаний которых отличаются на единицу (рис.1). Небольшие отклонения связаны с погрешностью обработки результатов. Линия тренда описана линейной зависимостью у(х).
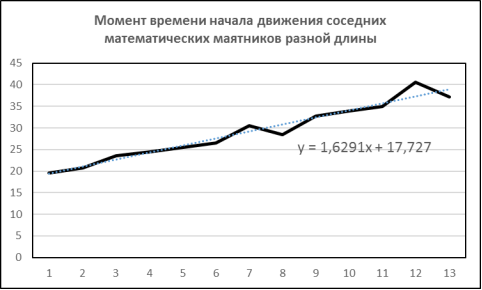
Рис.1. Моменты времени начала движения соседних маятников разной длины
Понятие о фазе и тем более о сдвиге фаз трудны в усвоении, желательно их наглядно продемонстрировать.
В нашем проекте математические маятники имеют нити разной длины, т. е. разные частоты колебаний. Таким образом, с их помощью можно наглядно получить картину фаз всех маятников во времени и продемонстрировать сложение 15 гармонических колебаний одного направления, но разных периодов колебаний. Для этого следует отклонить их на одинаковый угол от положения равновесия (например, линейкой) и привести в колебательное движение. Поскольку угол отклонения нити маятников от положения равновесия невелик, то можно считать, что мы наблюдаем гармонические колебания.
Таким образом, в ходе проведенной работы над проектом были рассмотрены особенности незатухающих свободных гармонических колебаний, разработана демонстрационная модель основных законов колебательного движения осцилляторов на примере нескольких математических маятников. Использование проектного метода позволило развить у курсантов познавательные и экспериментальные навыки, способность к самообразованию, целеустремленность и настойчивость для достижения поставленной цели.
Литература:
- Рекомендации по организации самостоятельной работы обучающихся. М.: РГТУ, 2013. 62 с.
- Штофф В. А. Моделирование и философия. М.: Наука, 1966. 304 с.
