В данной статье рассматривается создание автомата Мили на примере вычисления простейших логических операций. В ходе данной работы будет проведена оценка экономических затрат на построение схемы, оценку её быстродействия, а также проведен сравнительный анализ экономической эффективности этой задачи с автоматом Мура.
В предыдущей работе был подробно рассмотрен принцип построения автомата Мура. Реализация данного автомата не несет в себе никаких принципиальных отличий, за исключением основных правил моделирования этих автоматов.
Проведём аналогичные действия для синтеза автомата Мили, с учётом правил построения данного автомата.
Синтез автомата Мили слегка отличается [1] от синтеза автомата Мура: входные сигналы являются не только функциями состояний, но и логических условий. Также отличается способ обозначения состояний.
Формирование граф-схемы алгоритма. На этом этапе в ГСА вводятся состояния автомата Мили по следующим правилам:
‒ выход начальной и вход конечной вершин обозначаются состоянием а0
‒ выходы операторных вершин отмечаются состояниями начиная с а1. Если выходы нескольких операторных вершин объединяются они обозначаются одним состоянием.
Таблица 1
Прямая структурная таблица для автомата Мили
|
am |
K(am) |
as |
K(as) |
X |
Y |
F |
|
a0 |
00000 |
a1 |
00001 |
1 |
y1, y2, y4, y5 |
S0 |
|
a1 |
00001 |
a2 |
00010 |
1 |
y3, y6, y16, y17, y29, y10 |
S1 R0 |
|
a2 |
00010 |
a3 |
00011 |
1 |
y13, y24, y30, y6 |
S0 |
|
a3 |
00011 |
a4 |
00100 |
|
y21, y19, y30, y8, y18, y32, y9 |
S2 R1 R0 |
|
a6 |
00110 |
|
y15, y34, y11 |
S2 R0 |
||
|
a8 |
01000 |
|
y13, y17, y31, y10 |
S3 R1 R0 |
||
|
a4 |
00100 |
a5 |
00101 |
1 |
y21, y24, y29, y8, y15, y33, y4 |
S0 |
|
a5 |
00101 |
a11 |
01011 |
1 |
y21, y27, y29, y12 |
S4 S1 R2 |
|
a6 |
00110 |
a7 |
00111 |
1 |
y16, y27, y29, y12, y18, y33, y7 |
S0 |
|
a7 |
00111 |
a11 |
01011 |
1 |
y26, y22, y30, y10 |
S4 R2 |
|
a8 |
01000 |
a9 |
01001 |
1 |
y25, y33, y9 |
S0 |
|
a9 |
01001 |
a10 |
01010 |
1 |
y21, y24, y30, y8 |
S1 R0 |
|
a10 |
01010 |
a11 |
01011 |
1 |
y23, y35, y11 |
S0 |
|
a11 |
01011 |
a12 |
01100 |
|
y20, y32, y9 |
S2 R1 R0 |
|
a14 |
01110 |
|
y28, y34, y7 |
S2 R0 |
||
|
a12 |
01100 |
a13 |
01101 |
1 |
y16, y24, y29, y10 |
S0 |
|
a13 |
01101 |
a16 |
10000 |
|
y18, y33, y7 |
S4 R3 R2 R0 |
|
a19 |
10011 |
|
y13, y19, y30, y10, y18, y32, y7 |
S4 S1 R3 R2 |
||
|
a14 |
01110 |
a15 |
01111 |
1 |
y21, y27, y30, y8 |
S0 |
|
a15 |
01111 |
a0 |
00000 |
1 |
y23, y36, y7 |
R3 R2 R1 R0 |
|
a16 |
10000 |
a17 |
10001 |
1 |
y21, y17, y30, y8 |
S0 |
|
a17 |
10001 |
a23 |
10010 |
|
y21, y14, y29, y8 |
S1 R0 |
|
a18 |
10011 |
|
y21, y14, y29, y8 |
S1 |
||
|
a18 |
10010 |
a23 |
10111 |
1 |
y23, y37, y7 |
S2 S0 |
|
a19 |
10011 |
a20 |
10100 |
1 |
y21, y24, y29, y10 |
S2 R1 R0 |
|
a20 |
10100 |
a21 |
10101 |
1 |
y25, y33, y7 |
S0 |
|
a21 |
10101 |
a22 |
10110 |
1 |
y21, y24, y29, y8 |
S0 R1 |
|
a22 |
10110 |
a23 |
10111 |
1 |
y21, y24, y29, y8 |
S0 |
|
a23 |
10111 |
a24 |
11000 |
1 |
y23, y32, y7 |
S3 R2 R1 R0 |
|
a24 |
11000 |
a0 |
00000 |
1 |
y25, y22, y29, y8 |
R4 R3 |
Далее определим функции возбуждения памяти.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
После определения функций возбуждения памяти необходимо составить уравнения выходных сигналов в заданном базисе:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]()
![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]()
![]()
Проведем синтез дешифратора в заданном базисе, построив карту Карно для данного автомата.
Таблица 2
Карта Карно для дешифратора 5→25 для автомата Мили
|
|
000 |
001 |
011 |
010 |
110 |
111 |
101 |
100 |
|
00 |
|
|
|
|
|
|
|
|
|
01 |
|
|
|
|
|
|
|
|
|
11 |
|
* |
* |
* |
* |
* |
* |
* |
|
10 |
|
|
|
|
|
|
|
|
![]()
…………………………………………………
![]()
![]()
…………………………………………………
![]()
![]()
![]()
…………………………………………………
![]()
![]()
На рисунке 1 представлена принципиальная схема автомата Мили.
В данной работе для организации операционной части был выбран IMp [2] — автомат имеющий средние по цене и скорости показатели относительно других видов автоматов. Как видно из таблицы 3 количество элементов необходимых для реализации задачи на автоматах Мура и Мили отличаются. Схема автомата Мура для решения исходной задачи показала более высокую экономическую эффективность и более высокую скорость работы.
Также стоит отметить, что если реализовать эту задачу на других элементах, то результат может отличаться от полученного.
Таблица 3
Оценка аппаратных затрат
|
КА |
Количество дискретных элементов |
Триггер |
DC |
|
Мура |
134 |
5 |
5→30 |
|
Мили |
151 |
5 |
5→25 |
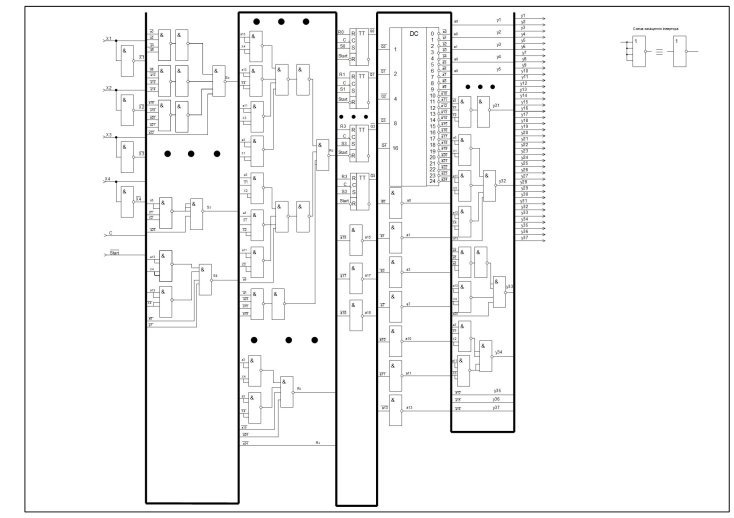
Рис. 1. Сокращённая схема автомата Мили
Литература:
- Баркалов А. А., Титаренко Л. А.. Прикладная теория цифровых автоматов.. — Донецк: ДонНТУ, Технопарк ДонНТУ УНИТЕХ, 2010. — 320 с.
- Баркалов А. А., Титаренко Л. А.. Синтез операционных устройств. — Донецк: РВА ДонНТУ, 2003. — 306 с.







