В работе исследован критерий оптимального распределения активной нагрузки между тремя агрегатами тепловой электрической станции с использованием программного комплекса Маtlab. Рассмотрен пример оптимального покрытия нагрузки энергосистемы всех суточных интервалов, обеспечивающих минимальный расход топлива.
Одной из основных задач, решаемых при управлении режимами электроэнергетических систем (ЭЭС) на современном этапе является оптимизация режимов работы тепловых электростанции (ТЭС). Она предусматривает определения оптимальных значений мощности, в регулируемых диапазонах агрегатов обеспечивающих минимальный расход топлива. В настоящее время используемые на практике методы и алгоритмы решения этой задачи имеют некоторые недостатки, связанные с ненадёжностью сходимости итеративного расчетного процесса при оптимизации тяжелых режимов электрических сетей с учетом программной реализации [1–3].
Для тепловой электрической станции, на которой работают m энергоблоков, баланс активных мощностей запишется в виде:
 ,
,
где Рi — активная мощность, генерируемая i-ым энергоблоком;Рн — нагрузка станции; m — количество энергоблоков.
Суммарный расход топлива на электростанции составит:
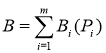 .
.
Здесь Вi — расход топлива на генерацию мощности Рi на i-том энергоблоке.
Для получения минимального расхода топлива (В) на ТЭС с учётом соблюдения баланса мощностей воспользуемся методом Лагранжа с функцией:
где — некоторый постоянный коэффициент, называемый множителем Лагранжа.
Минимум L можно определить, взяв частные производные от L по Рi и приравняв их нулю:
![]()
![]()
![]() .....
..... ![]()
Отсюда:
![]() .
.
Производная ![]() — это относительный прирост расхода топлива (ОПРТ) на i -ом энергоблоке ТЭС.
— это относительный прирост расхода топлива (ОПРТ) на i -ом энергоблоке ТЭС.
Тогда критерием оптимального распределения нагрузки между агрегатами ТЭС является
b1 = b2 = … = bm = idem,
то есть равенство ОПРТ всех энергоблоков станции.
Практическое решение задачи получения минимального расхода топлива на ТЭС можно осуществить по следующему алгоритму:
- По заданным характеристикам ОПРТ энергоблоков станции bi=f(Pi) произвести их суммирование и получить эквивалентную характеристику ТЭС bс = f(Pс).
- Для рассматриваемой нагрузки электростанции на эквивалентной характеристике определяется bс по значению Рс.
- На характеристике ОПРТ каждого энергоблока отыскиваются мощности Р1, Р2, …, Рm, соответствующие значению Рс.
Пункт 1 выполняется следующим образом (рис. 1).
Первая точка суммарной характеристики — это точка с координатами: [PCmin = P1min + P2min + P3min; bCmin], где bCmin — наименьшее значение ОПРТ из всех блоков. Далее задаются значением ![]() и проводят прямую, параллельную оси абсцисс, по всем трём графикам до пересечения с ними. Полученные значения
и проводят прямую, параллельную оси абсцисс, по всем трём графикам до пересечения с ними. Полученные значения ![]() и
и ![]() суммируются, в результате чего определяется
суммируются, в результате чего определяется ![]() :
:
![]()
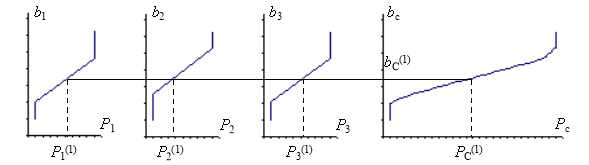
Рис. 1. Характеристики ОПРТ ТЭС
На эквивалентной характеристике ОПРТ ТЭС таким образом получена точка с координатами [![]() ;
;![]() ]. Повторяется эта операция, задаваясь значениями
]. Повторяется эта операция, задаваясь значениями ![]() ,
, ![]() , до получения
, до получения
PCmax = P1max + P2max + P3max.
Построив суммарную характеристику ОПРТ ТЭС, можно теперь, отложив на оси активных мощностей Рс, определить bc и по нему обратным ходом получить Р1, Р2, Р3, то есть выполнить пункты 2 и 3.
На основе полученного вывода разработан программный комплекс на базе Маtlab. Программа составлена для оптимального распределения графиков суммарных активных нагрузок энергосистемы между тепловыми электрическими станциями. Она позволяет определить оптимальные графики нагрузок всех электростанций, участвующих в оптимизации, с учетом технологических ограничений. Программа предусматривает выполнения оптимизации в условиях наличия в энергосистеме множества тепловых электростанций.
Она дает возможность определить оптимальные режимы электростанций и энергосистемы с высокой точностью и надежностью [4].
Эффективность данного алгоритма исследовано на примере в оптимальном покрытии суммарного графика нагрузки энергосистемы (табл. 1) за цикл регулирования, состоящий из пяти интервалов, тремя ТЭС со следующими расходными характеристиками:
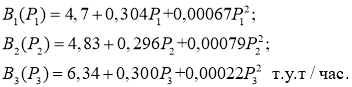
Таблица 1
Суммарный график нагрузки энергосистемы
|
Время суток, ч |
0–6 |
6–14 |
14–20 |
20–22 |
22–24 |
|
Суммарная нагрузка PН, МВт |
330 |
520 |
580 |
540 |
420 |
Таблица 2
Оптимальное покрытие исходного графика нагрузки
|
Время суток, ч |
0–6 |
6–14 |
14–20 |
20–22 |
22–24 |
|
|
РС, МВт |
330 |
520 |
580 |
540 |
420 |
|
|
1 ТЭС |
Р1, МВт |
85,0000 |
126,6630 |
159,1287 |
137,4849 |
85,0000 |
|
В1, т.у.т./ч |
35,3807 |
53,9547 |
70,0408 |
59,1598 |
35,3807 |
|
|
2 ТЭС |
Р2, МВт |
90,0000 |
112,4863 |
140,0205 |
121,6644 |
90,0000 |
|
В2, т.у.т./ч |
37,8690 |
48,1219 |
61,7646 |
52,5364 |
37,8690 |
|
|
3 ТЭС |
Р3, МВт |
155,0000 |
280,0000 |
280,0000 |
280,0000 |
245,0000 |
|
В3, т.у.т./ч |
58,1255 |
107,5880 |
107,5880 |
107,5880 |
93,0455 |
|
Результаты оптимального покрытия исходного графика нагрузки энергосистемы тремя расчетными ТЭС приведены на рисунке и табл. 2.
В результате оптимального покрытия графика нагрузки суммарный расход условного топлива в расчетных ТЭС за цикл регулирования составляет 4673,087 т.у.т.
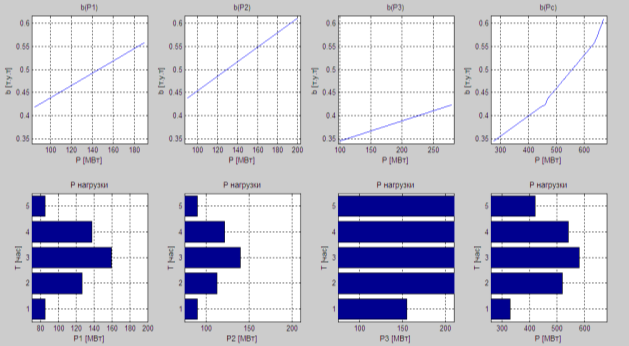
Рис. 2. Результаты расчета в программе Маtlab
Вывод
Данная программа может быть использована диспетчерскими пунктами энергосистем для оптимального управления их режимами, также при проведении лабораторных и практических занятий по курсам «Электрические сети и системы», «АСУ и оптимизация режимов электрических станций и систем».
Литература:
- Фазылов Х. Ф., Насыров Т. Х. Установившиеся режимы электроэнергетических систем и их оптимизация. Ташкент. Изд-во Молия, 1999. С.370
- C. K. Panigrahi, P. K. Chattopadhyay and U. Prasad, “Linear Programming Approach for Bidding of Generators in Restructured Power Industry, ”International Electrical Engineering Journal, 2012, vol. 3, no. 1, pp. 589–594.
- Ю. Н. Руденко., В. А. Семенова. Автоматизация диспетчерского управления в электроэнергетике. Москва. Изд-во МЭИ, 2000. С.648.
- Гайибов Т. Ш., Реймов К. М. Программа «TESGES» для оптимального покрытия графиков нагрузок энергосистемы тепловыми и гидравлическими электрическими станциями. /Программа для ЭВМ/ № DGU 03033. 10.02.2015 г. Агентство по интеллектуальной собственности Республики Узбекистан.







