Приводится численное исследование изменения скорости и диаметра жидкой горящей капли при ее взаимодействии с акустическим потоком газа в длинной цилиндрической трубе. При моделировании учитывают аэродинамическое взаимодействие капли с газовым потоком и процессы испарения и горения. Расчеты проводились для этилового спирта, которые реагируют с кислородом воздуха. Исследованы влияния начальных значений диаметра капли, ее положения и скорости на изменение ее диаметра. Построены зависимости по результатам расчетов. Приведенная методика позволяет подобрать такие значения геометрических и термодинамических параметров трубки Рийке, которые были бы оптимальны для рабочего процесса горения жидкого топлива.
Ключевые слова: трубка Рийке, теплоподвод, время жизни капли, изменение диаметра
Рассматривается цилиндрическая труба длины L, диаметра d, причем d<<L. Ось трубы 0 наклонена к горизонту под углом . В сечении ![]() имеется теплоподвод шириной
имеется теплоподвод шириной ![]() (трубка Рийке). Схема трубы и положение капли представлены на рис. 1.
(трубка Рийке). Схема трубы и положение капли представлены на рис. 1.
Приведем условия моделирования поведения капли в акустическом поле трубы
- Рассматривается трёхмерное движение капли в одномерном акустическом поле трубы.
- Капли в трубе не дробятся, предварительная подготовка их к испарению (дробление, прогрев, самовоспламенение) происходит в резонаторной трубе.
- Обратные токи отсутствуют. Процесс испарения поддерживается за счёт самовоспламенения компонентов непосредственно после поступления их в трубу.
- Рассматривается движение капли наибольшего диаметра, образованной в результате газодинамического распыла. Считается, что рассматриваемая капля изолирована от более мелких капель и имеет определённую начальную скорость.
- В процессе движения капель не происходит их коалесценции (соприкосновения).
- Испаряющиеся капли не влияют на характер движения газовой среды.
- Лучистый теплообмен при нагреве и испарении капель не учитывается.
- Начальная температура капель и газа равна той, с которой они поступают в камеру сгорания.
- Колебания давления в камере не влияют на температуру в ней.
При решении задачи рассмотрим частный случай — труба закрыта с одного конца. Давление на входе и выходе полагаются постоянным. Решение строится на совместном решении системы волновых уравнений, уравнений движения и испарения [1–4]. В статье [5] представлены опыты на экспериментальной установке аналогичной задачи для исследования гидродинамических параметров на начальном участке течения жидкости.
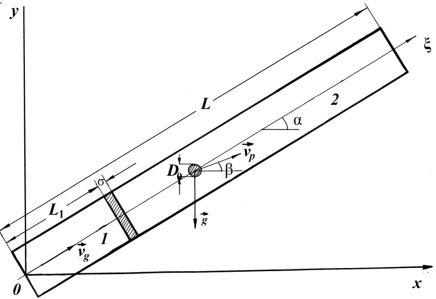
Рис. 1. Схема трубы
Расчеты проводились для случая испарения капель дизельного топлива в кислороде воздуха. Приведем конкретные значения геометрических и термодинамических параметров: ![]() =2,5 м,
=2,5 м, ![]() =0,5 м,
=0,5 м, ![]() =0,2 м,
=0,2 м, ![]() =633,5 К,
=633,5 К, ![]() =293 K,
=293 K, ![]() =293 K,
=293 K, ![]() =45°,
=45°, ![]() =0,44310–4,
=0,44310–4, ![]() =45°,
=45°, ![]() =0,0691Дж/(мК),
=0,0691Дж/(мК), ![]() =29 кг/кмоль,
=29 кг/кмоль, ![]() =1.4,
=1.4, ![]() =8314 Дж/(кмоль∙К),
=8314 Дж/(кмоль∙К), ![]() =1880 Дж/(кг∙К),
=1880 Дж/(кг∙К), ![]() =1,13910–4 м3/с,
=1,13910–4 м3/с, ![]() =860 кг/м3,
=860 кг/м3, ![]() =9.8 м/с2,
=9.8 м/с2, ![]() =381000 Дж/кг,
=381000 Дж/кг, ![]() =1,29 г/м3,
=1,29 г/м3, ![]() =0,0283
=0,0283![]() м2/с.
м2/с.
При заданных геометрических параметрах и ![]() = 0,71,
= 0,71, ![]() = 0,11 и замеренных значениях
= 0,11 и замеренных значениях ![]() = 293 K,
= 293 K, ![]() = 1025 K значение
= 1025 K значение ![]() = 0,3933 м-1 получается из решения волнового уравнения [6, c. 182], а определенное экспериментально максимальное давление в начале трубы
= 0,3933 м-1 получается из решения волнового уравнения [6, c. 182], а определенное экспериментально максимальное давление в начале трубы ![]() = 5120 Па.
= 5120 Па.
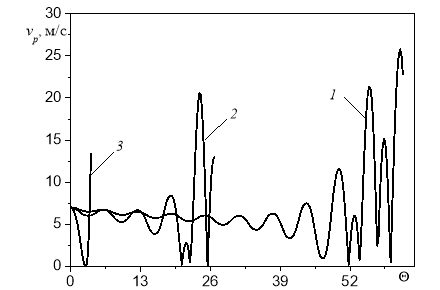
На рис. 2 представлены изменения модуля скорости капли при начальной скорости ![]() =7м/с и различных значениях диаметра в зависимости от безразмерного времени . При испарении скорость капли начинает пульсировать.
=7м/с и различных значениях диаметра в зависимости от безразмерного времени . При испарении скорость капли начинает пульсировать.
|
|
|
Рис. 2. Изменение модуля скорости капли при |
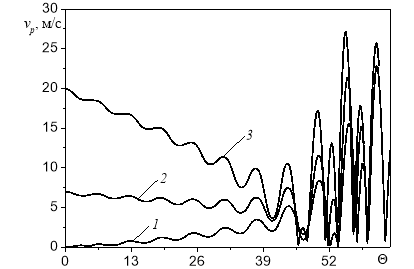
На рис. 3 представлены изменения модуля скорости капли для различных значений скорости в зависимости от безразмерного времени . При увеличении начальной скорости капли пульсации усиливаются.
|
|
|
Рис. 3. Изменение модуля скорости капли D0=500 мкм для различных значений скорости в зависимости от безразмерного времени: 1 — |
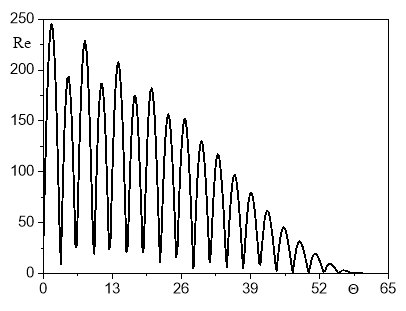
На рис. 4 представлены изменения числа Re в зависимости от безразмерного времени . Для приведенных выше значений параметров число Re совершает затухающие колебания.
|
|
||
|
Рис. 4. Зависимость числа Re от безразмерного времени |
||
На рис.5 представлена зависимость диаметра капли от безразмерного времени при постоянной скорости.
|
|
|
Рис. 5 Изменение диаметра капли в зависимости от безразмерного времени при постоянной скорости |

Рис. 6. Изменение диаметра капли в зависимости от безразмерного времени при различных значениях начальной скорости
По рис.6 можно судить о времени жизни капли ![]() = 700 мкм при различных значениях начальной скорости. Увеличение
= 700 мкм при различных значениях начальной скорости. Увеличение ![]() интенсифицирует взаимодействие капли с потоком и сокращает время ее жизни, но не очень сильно.
интенсифицирует взаимодействие капли с потоком и сокращает время ее жизни, но не очень сильно.
Литература:
- Carvalho J. A., Mcquay M. Q. and Gotac P. R. The Interaction of Liquid Reacting Droplets with the Pulsating flow in a Rijke-Tube Combustor. Combustion and Flame. 108: 87–103, 1997.
- Зверев И. Н., Смирнов Н. Н. Газодинамика горения. М: Изд-во МГУ, 1987, 308 с.
- Нигматулин Р. И. Динамика многофазных сред. Часть 1. М: Наука, 1987, 464 с.
- Самарский А. А., Попов Ю. П. Разностные методы решения задач газовой динамики. М.: Наука, 1980. 352 c.
- Шарипов И. И., Салимханов М. М. Исследование течения жидкости на начальном участке контактного устройства для струйно-барботажной колонны // Молодой ученый. — 2017. — № 4. C. 85–89.
- Попкова О. С., Медведева П. В., Шаймухаметова А. Ш., Шаймухаметов М. И. Определение параметров горящей капли при ее взаимодействии с акустическим потоком газа в трубке// Молодой ученый. — 2015. — № 24. C. 181–184.