В работе рассматривается формализация проблемы синтеза интегрированной системы безопасности в виде задачи целочисленного программирования с использованием метода экспертных оценок для определения вычислительных параметров.
Ключевые слова: интегрированные системы безопасности; экспертные оценки; метод Саати; задача о минимальном покрытии множества, метод Гомори
Безопасность предприятия либо иного объекта является одной из важнейших задач. При построении системы безопасности предприятия приоритетна проблема оптимального выбора средств охранной сигнализации, контроля доступа и видеонаблюдения, являющихся основой обнаружения нарушителя. Для решения поставленных задач в настоящее время на объектах устанавливаются интегрированные системы безопасности (ИСБ), представляющие собой аппаратно-программный комплекс технических средств с технической, программной, информационной совместимостью. При этом в состав ИСБ могут входить компоненты различных производителей. Задачей специалистов становится определение оптимального набора элементов оборудования для оснащения конкретного объекта [1].
Пусть для ИСБ задано множество технических параметров. Обозначим через ![]() - совокупность требований, предъявляемых к ним. Далее,
- совокупность требований, предъявляемых к ним. Далее,![]() — множество элементов оборудования, т.ч. каждому
— множество элементов оборудования, т.ч. каждому ![]() соответствует некоторое подмножество требований
соответствует некоторое подмножество требований ![]() . При этом можно утверждать, что для каждого объекта
. При этом можно утверждать, что для каждого объекта ![]() выполнено требование
выполнено требование ![]() или выполнены функции из
или выполнены функции из ![]() с определенным качеством. Множество всех
с определенным качеством. Множество всех ![]() назовём покрытием множества R, если выполнено условие:
назовём покрытием множества R, если выполнено условие: ![]() .
.
Вводим матрицу ![]() т.ч.:
т.ч.: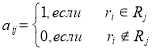 .
.
Другими словами, ![]() 1, если требование
1, если требование ![]() выполнено (покрыто), и
выполнено (покрыто), и ![]() в противном случае.
в противном случае.
Полагаем, что ![]() — стоимость требуемого элемента оборудования, тогда целевое значение функции
— стоимость требуемого элемента оборудования, тогда целевое значение функции ![]() равно минимальной суммарной стоимости всех компонентов ИСБ, удовлетворяющих полной совокупности требований, предъявляемых к системе.
равно минимальной суммарной стоимости всех компонентов ИСБ, удовлетворяющих полной совокупности требований, предъявляемых к системе.
Таким образом, задача определения оптимальной структуры, образованной элементами ![]() с учетом реализации всего набора требований
с учетом реализации всего набора требований ![]() может быть сформулирована как задача целочисленного программирования следующего вида:
может быть сформулирована как задача целочисленного программирования следующего вида:
![]() (1)
(1)
при условиях:
![]() .(3)
.(3)
Другими словами, задача определения оптимальной структуры сводится к целочисленной минимизации целевой функции (1) при ограничениях (2),(3).
Пусть ![]() - эффективность элементов системы, тогда задача максимизации:
- эффективность элементов системы, тогда задача максимизации:
![]() (4)
(4)
при условиях:
![]() (5)
(5)
![]() ,(6)
,(6)
интерпретируется как задача определения структуры системы, обладающей максимальной эффективностью.
Таким образом, рассматриваемая задача синтеза ИСБ сводится к решению задачи о минимальном покрытии множества R. В ряде случаев рассматриваются обобщённые задачи о покрытии, тогда ограничение (5) имеет вид:
![]() где
где ![]() ,(7)
,(7)
то есть вводится требование, чтобы i-ое требование было покрыто не менее
Для определения величины b могут быть использованы известные методы нахождения экспертных оценок, например, метод Саати, метод парных сравнений и нормализации по каждому условию ![]() . Используем парные сравнения. Для того, чтобы зафиксировать результат сравнения пары альтернатив из множества
. Используем парные сравнения. Для того, чтобы зафиксировать результат сравнения пары альтернатив из множества ![]() , будем использовать шкалу превосходства, предложенную Саати, следующего вида: 1- равноценность, 3-умеренное превосходство, 5-сильное превосходство, 7-очень сильное превосходство, 9-высшее превосходство. Пусть, m=4. Лицо, принимающее решение (ЛПР) попарно сравнивает альтернативы, оформляя результат сравнения в виде таблицы следующего вида:
, будем использовать шкалу превосходства, предложенную Саати, следующего вида: 1- равноценность, 3-умеренное превосходство, 5-сильное превосходство, 7-очень сильное превосходство, 9-высшее превосходство. Пусть, m=4. Лицо, принимающее решение (ЛПР) попарно сравнивает альтернативы, оформляя результат сравнения в виде таблицы следующего вида:
Таблица 1
|
|
|
|
|
|
|
|
1/1 |
1/4 |
4/1 |
1/6 |
|
|
4/1 |
1/1 |
4/1 |
1/4 |
|
|
1/4 |
1/4 |
1/1 |
1/5 |
|
|
6/1 |
4/1 |
5/1 |
1/1 |
Здесь дробь на пересечении i-ой строки и j-го столбца (например, 4/1) выражает мнение ЛПР, трактующееся в виде: альтернатива ![]() важнее альтернативы
важнее альтернативы ![]() в 4 раза.
в 4 раза.
Переведем обыкновенные дроби в десятичные. Приходим к таблице результатов парных сравнений:
Таблица 2
|
|
|
|
|
|
Сумма по строке |
|
|
1,0 |
0,25 |
4,00 |
0,17 |
5,42 |
|
|
4,00 |
1,00 |
4,00 |
0,25 |
9,25 |
|
|
0,25 |
0,25 |
1,00 |
0,20 |
1,70 |
|
|
6,00 |
4,00 |
5,00 |
1,00 |
16,00 |
|
|
Сумма строчных сумм |
32,27 |
|||
Нормируем суммы так, чтобы их сумма равнялась 1, для чего делим сумму по каждой строке на 32,27. Получаем:
Таблица 3
|
|
|
|
|
|
Сумма по строке |
|
|
1,0 |
0,25 |
4,00 |
0,17 |
0,116 |
|
|
4,00 |
1,00 |
4,00 |
0,25 |
0,247 |
|
|
0,25 |
0,25 |
1,00 |
0,20 |
0,060 |
|
|
6,00 |
4,00 |
5,00 |
1,00 |
0,577 |
|
|
Сумма |
1,00 |
|||
Приведенные нормированные суммы равны оценкам альтернатив (![]() ) по критерию важности с точки зрения ЛПР. Подставляя полученные значения в (7), получаем задачу целочисленного программирования, для приближенного решения которой может быть применен широкий спектр вычислительных методов [2,3].
) по критерию важности с точки зрения ЛПР. Подставляя полученные значения в (7), получаем задачу целочисленного программирования, для приближенного решения которой может быть применен широкий спектр вычислительных методов [2,3].
Таким образом, предложенные математические модели позволяют на основе анализа требований, предъявляемых к обеспечению безопасности объекта, определить оптимальный набор оборудования из различных подсистем, предлагаемых на рынке.
Литература:
- Белокуров С. В., Зыбин Д. Г., Джоган В. К., Сидельников А. П. Моделирование процессов выбора для защиты информации в интегрированных системах безопасности на основе экспертных знаний.- Воронежский институт ФСИН России.- Воронеж, 2014.
- Нгуен Минь Ханг. Применение генетического алгоритма для задачи нахождения покрытия меножества.- Вычислительный центр им. А. А. Дородницына РАН. Москва.- Динамика неоднородных систем, 2008.
- Царькова Е. Г., Бырков А. Ю., Петрова О. Е. Математическая модель задачи управления процессом обучения слушателей учебного центра и её решение численными методами.- Фундаментальные и прикладные исследования: актуальные вопросы, достижения и инновации. Сборник статей победителей международной научно-практической конференции.- МЦНС ”Наука и Просвещение”, 2016.







