О реализации программного движения алгоритмом управления по принципу обратной связи



Рассмотрим систему, состоящую из исполнительной электрической машины (ЭМ), механизма передачи вращательного движения с коэффициентом редукции i₁ и объектом управления (ОУ). В качестве исполнительного элемента принимается электрическая машина (ЭМ) постоянного тока с независимым возбуждением. Обозначим через момент инерции якоря электрической машины (ЭМ), J_p — момент инерции редуктора. Пусть угол поворота вала электрической машины (ЭМ) (якоря) есть _я. Если М_н — момент, прикладываемый к объекту управления (ОУ) со стороны электрической машины (ЭМ) в режиме двигателя, то уравнение вращательного движения, согласно работам Крутько П. Д. [1–4], а также Джолдасбекова У. А. и Молдабекова М. М. [5, 6], можно записать в виде:

,(1)

Где q есть n – мерный вектор столбец обобщенных координат, характеризующих конфигурацию системы; A(q) — матрица инерции подвижных элементов системы; – матрица кориолисовых и центробежных сил инерции, а также сил трения; C(q) — матрица, обусловленная силами тяжести; M – электромагнитный момент, развиваемый электрической машиной (ЭМ).

Систему (1) можно привести к одному уравнению, если использовать кинематическое соотношение и провести пересчет моментов, стоящих в правой части первого уравнения, к второй. Выполняя указанные действия, получим:

(2)

Где

Электрическая часть системы, согласно работам Чиликина М. Г. и Сандлера А. С. [7], Лунца Я. Л. [8], Крутько Л. Д. [1–4], описывается уравнениями:

,

M = K_mI,(3)

,

Где L, R₁ — индуктивность и активное сопротивление якорной цепи; I, U — ток и напряжение цепи якоря; K_w, K_m — коэффициент противо-ЭДС и вращательного момента; к_y, _y – коэффициент усиления и постоянная времени усилителя; — входное напряжение усилителя.

Вводим электрическую постоянную времени:

Обычно, согласно Крутько П. Д. [1–4]_y<<_э. Отсюда . Тогда в качестве управляющей функции выступает напряжение и. Умножая первое уравнение (3) на , приведем его к виду:

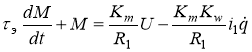(4)

Наряду с полной моделью (4) будем использовать далее так же упрощенную модель, в которой не учитываются процессы в якорных цепях исполнительных электрических машин ЭМ. В (4) принимая электрическую постоянную времени _э=0, будем иметь:

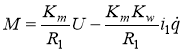,(5)

При безынерционном усилителе (_у=0) из (2), (3) получим:

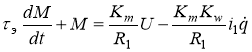(6)

Следуя Крутько Л. Д. [1–4], проблему управления движением сформулируем следующим образом: в начальный момент времени t=0 состояние управляемой системы характеризуется значениями:

q_j(o)=q_jo,,(j=1,…,n)(7)

Требуется синтезировать такой алгоритм вычисления управляющих напряжений

, (j=1,…,n)(7a)

при котором, управляемая система перемещается за конечное время из точки (7) в окрестность траектории:

q_j^* = q_j(t), (j=1,…,n)(8)

и остается в этой окрестности при последующем движении.

Согласно сформулированным требованиям, следуя Бойчуку Л. М. [9], отклонения _j(t)=q_j⁰-q_j должны подчиняться в процессе управления дифференциальным уравнениям:

, (j=1,…,n)(9)

Где — положительные константы.

Следуя Крутько Л. Д. [1–4], и на основании (9) заключаем, что программное движение (8) будет реализовано только в том случае, когда ускорения изменяются по закону:

, (j=1,…,n)(10)

Следовательно, искомые законы (7а) формирования управляющих напряжений, которые обеспечивают реализацию программного движения (8), могут быть найдены подстановкой ускорения из (10) в (2). Такая подстановка дает

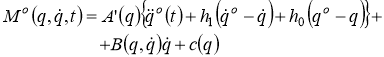(11)

Где h_e – диагональные матрицы

h_e = diag {h_1e, h_2e,…,h_ne}, (e=o,…,1)

Для окончательного решения задачи синтеза, т. е. для определения закона формирования управляющих напряжений, подставим выражение М⁰ из (11) в соотношение (5):

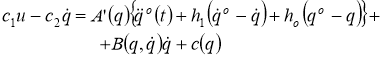(12)

Где C_m = diag {C_m1, C_m2,…,C_mn},(m=1,…,2), элементы которой ,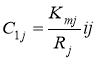

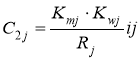
(j=1,…,n)

и откуда

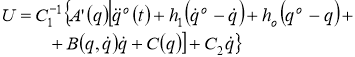(13)

Таким образом, основу алгоритма управления по принципу обратной связи составляют соотношения (11) и (12). На рис.1 представлена структурная схема замкнутой системы автоматического управления.

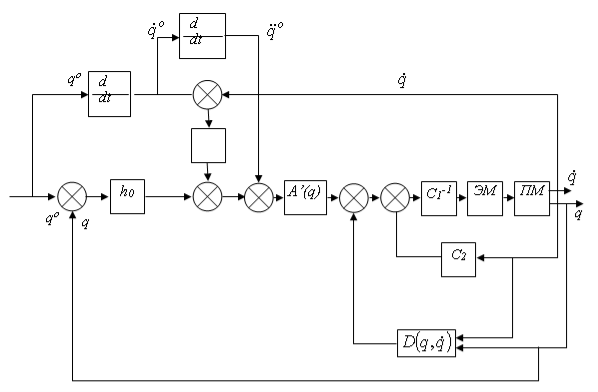
Рис. 1.

Здесь

Из рисунка видно, что замыкание контуров приводных электрических машин ЭМ осуществляется по переменным , значения которых используются при вычислении сигналов, C(q) и C₂q, а также при определении рассогласований по положению и скорости. На практике вместо производных могут использоваться угловые скорости , (j=1,…,n). Управляющие напряжения для каждой исполнительной электрической машины ЭМ вычисляются согласно (13) по текущим значениям всех управляемых кинематических переменных и скоростей их изменения q_j(t),, т. е. управляющее напряжение на отдельный привод формируется с учетом состояния управляемого механизма по всем степеням подвижности.

Из работ Малкина И. Г. [10] и Меркина Г. Д. [11] известно, что для устойчивой реализации этого алгоритма необходимо и достаточно, чтобы корни характеристического уравнения системы (9)

P²+h₁p+h_o=0,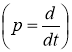

имели отрицательные вещественные части. Поскольку, по условию, h₁,h_o — положительные постоянные, необходимые и достаточные условия устойчивости

Reh_e<0(e=0,…,1) выполняются для любых h₁, h_o.

Литература:

1. Крутько Л. Д. Алгоритмы адаптивного управления исполнительными системами манипуляторов // Изв. АН. СССР. Техническая кибернетика. — 1988. — № 4. – С. 3–13.
2. Крутько П. Д. Обратные задачи динамики управляемых систем. Линейные модели. М.: Наука, 1983. – 271 с.
3. Крутько П. Д., Лакота Н. А. Метод обратных задач динамики в теории конструирования алгоритмов управления манипуляционных роботов. Осуществление назначенных траекторий // Изв. АН СССР. Техническая кибернетика. — 1978. № 4. – С. 190–199.
4. Крутько П. Д., Лакота Н. Я. Метод обратных задач динамики в теории конструирования алгоритмов управления манипуляционных роботов. Задача стабилизации // Изв. АН СССР. Техническая кибернетика. — 1987. — № 3. – С. 127–135.
5. Джолдасбеков У. А., Молдабеков М. М. Уравнения динамики манипуляционных устройств высоких классов // В сборнике: Математическое моделирование задач теории механизмов и машин. — Алма-Ата. 1987. – С. 3–9.
6. Джолдасбеков У. А., Бияров Т. Н. Динамика двухзвенного робота — манипулятора // В сборнике: Вопросы теории механизмов и управления машинами. Алма-Ата, 1986. – С. 3–8.
7. Чиликин М. Г., Сандлер А. С. Общий курс электропривода, М.: Энергоиздат, 1981. – 576 с.
8. Лунц Я. Л. Введение в теорию гироскопов. — М.: Наука, 1972. – 296 с.
9. Бойчук Л. М. Метод структурного синтеза нелинейных систем автоматического управления, М.: Энергия, 1972. — 112 с.
10. Малкин И. Г. Теория устойчивости движения. – М.: Наука, 1966. – 532 с.
11. Меркин Г. Д. Введение в теорию устойчивости. М.: Наука,1987. – 304 с.