Пусть прямоугольная декартова система координат связана с пластиной так, что движение происходит в плоскости Х, Z. Внешние поверхности пластины задаются условиями Z = h1 и Z = — h 2. Пусть верхняя пластина, определенная условием 0 < Z < h1, характеризуется величинами 
. 
. [1,3]
Уравнения плоской деформации теории упругости имеют вид:
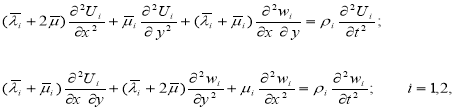
где U и w — компоненты смещения по х и z.
Граничные условия для пластины со свободными границами при у=h1 и у=h2 и жестко связанной при у = 0 имеют вид:
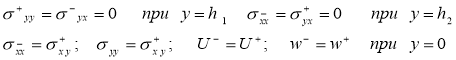(1)
Чтобы исследовать распространение серии волн, положим
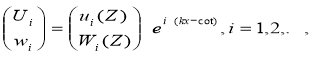(2)
где k — волновое число, 
— комплексная частота; С = СR+iCI — комплексная фазовая скорость. Подставляя решение задачи (2) в (1), получаем
- амплитудная комплексная векторная функция [4]
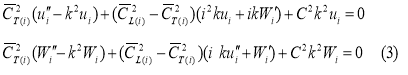
Теперь граничные условия (2) преобразуются в виде:
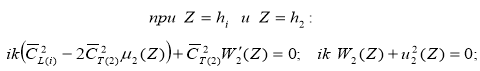
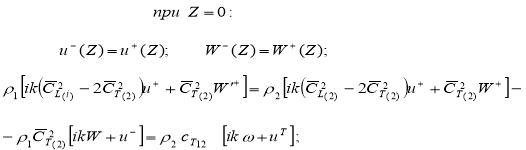(4)
где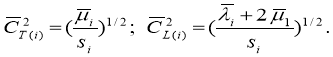 
Итак, имеем два уравнения (3) и (4) второго порядка для двух областей и восьми граничных условий. Будем решать задачу, не сводя её к уравнению четвертого порядка. Все рассуждения приводятся для одного слоя. Находим частное решение системы (3) в виде:
(5)
Подставляя (5) в (3) и (4) сокращая на е rZ, получим алгебраическую систему. Она имеет непрерывное решение, если ее определитель равен нулю, т. е.
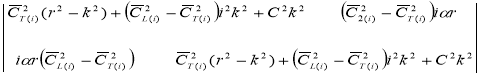=0. (6)
Уравнение (2.10) можно решить относительно ri,так как
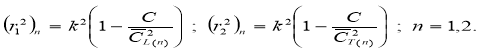(7)
Найдя ri (i=1,2,... 4), вернемся к системе для Аi и Вi и решим ее для каждого значения ri. В результате найдём четыре частных решения вида (5) (для первого и второго слоев)
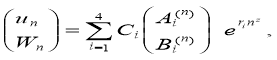n = 1,2.
Здесь А(j)i и В(j)i (j = 1,2; i = 1,2,...., 4) — линейно-зависимые. С(1)i и С(2)i — произвольные постоянные, которые определяются из граничных условий (2). Выражения для перемещений имеют вид:
+
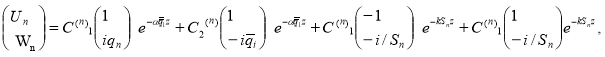
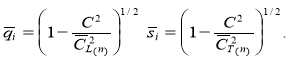
Следовательно, для (4) получим совокупность восьми граничных условий, которые приводят к восьми однородным уравнениям с восемью неизвестными С(1)j и С(2)j (j =1,4). Для того, чтобы такая система уравнений имела нетривиальные решения, определитель коэффициентов должен быть равен нулю. Последнее условие дает зависимость частот (ωR) и коэффициентов демпфирования (поглощения) (ωI) от волнового числа (или других параметров системы) [5]. Уравнение дисперсии имеет вид:
где
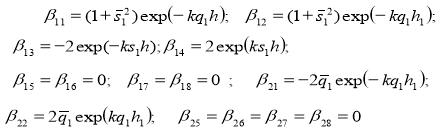
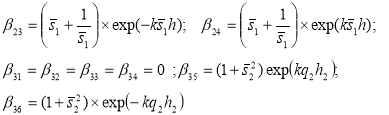
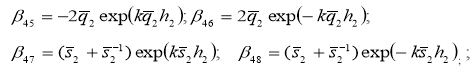
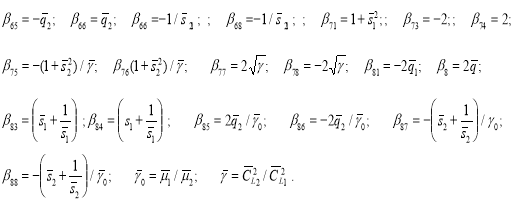
Теперь это уравнение будет решено относительно ω/k для различных значений k.
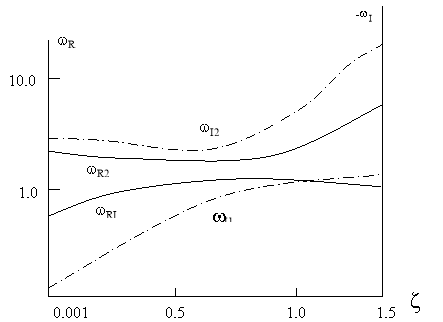
Рис. 1. Изменение собственных частот от волнового числа. Диссипативно однородная система
Численные расчеты. Корни уравнения рассчитаны на ЭВМ при следующих значениях безразмерных параметров:
С2L1=0.622; С2L2=3.360; С2T1=3.360; С2T2 = 0.776; μ1=0.170; μ 2=0.830:
Результаты представлены графически в виде кривых зависимостей (ξ = kH, H = h1+h2) от ω для h1 / H =0.5. Рассмотрим два варианта системы.
В первом варианте рассмотрена однородная система.
Результаты расчетов приведены на рис 1. Зависимость частот (ωR) и коэффициентов демпфирования от ξ оказалась монотонной, причем характер ее одинаков для частот коэффициентов демпфирования.
Во втором варианте рассмотрена неоднородная система: первый слой упругий; остальные параметры совпадают с указанными выше [2].
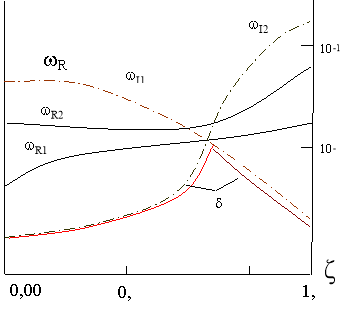
Рис. 2. Изменение собственных частот от волнового числа. Диссипативно неоднородная система
Результаты расчетов, представлены на рис. 2. Зависимость частот от ξ оказалась такой же, как и для диссипативно однородной системы: соответствующие кривые совпадают с точностью до 5 %.
Что же касается коэффициентов демпфирования, то их поведение изменилось радикальным образом: зависимость ωI ~ ξ стала немонотонной. Глобальный коэффициент демпфирования при указанном характерном значении ξ имеет ярко выраженный максимум [6].
Литература:
- Болтаев З. И. Распространение линейных гармонических волн в протяженных плоских и цилиндрических телах с учетом вязкоупругих свойств материала. Ташкент. Фан.-2013.-136с.
- Голоскоков Д. П. Уравнения математической физика. Решение задач в системе MAPLE.-СПб: Питер,2004.-539с.
- Каюмов С. С., Сафаров И. И. Распространение и дифракция волн в диссипативно–неоднородных цилиндрических деформируемых механических систем. Ташкент: ФАН, 2002г,
- Кристенсен Р. Введение в теорию вязкоупругости. Мир, 1974
- Сафаров И. И., Тешаев М. Х., Болтаев З. И. Волновые процессы в механическом волноводе. LAP LAMBERT Academic publishing (Германия). 2012.,217 с.
- Сафаров И. И. Распространения волн в слое, лежащем в вязкоупругом полупространстве.- Тезисы докладов конфер. «Опыт применения композитных материалов в сельскохозяйственном машиностроении», Чернягов, 1985, с.91–92.
