Каждая задача может служить многим конкретным целям обучения. И все же в обучении математики главная цель задач — развивать математический стиль мышления учащихся, заинтересованность их математической деятельностью. Достижение этих целей с помощью одних стандартных задач невозможно.
С этой целью просто необходимо широкое применение задач с практическим содержанием. Это воспитывает интерес к предмету: математика уже не кажется сухой и скучной наукой. Использование задач с практическим содержанием создает условия для реализации на этапе введения нового материала межпредметных связей, связи обучения математике с жизнью.
В техникуме связь математики с предметами производственного цикла особенно важна. Покажем точки соприкосновения математики с разними специальностями, например, с электромеханикой.
Рабочие этого профиля обеспечивают создание, воспроизводство и эксплуатацию технических систем, функционирующих на основе реализации теорий электростатики и электродинамики.
Для понимания рабочими этого профиля профессий принципов действия оборудования обязательна система понятий, опирающаяся на общность знания по математике и электротехнике. Например, при изучении темы «Переменный ток» широко используются знания тригонометрических функций. Тригонометрические тождества используются при выводе формулы мгновенного знания мощности в цепи переменного тока, включающей активное и реактивное сопротивление (при наличии в цепи индуктивности).
При изучении машин переменного тока используются логарифмическая и степенная функции. Любое электротехническое устройство и его элементы имеют определенную форму, т. е. характеризуются такими параметрами, как длина, сечение, объем, поверхность и т. д. Поэтому выбор размеров этих устройств требует знаний геометрических соотношений между указанными параметрами.
При изучении темы «Исследование функций» можно использовать систему знаний с графиками различных зависимостей (например, поведение тока в катушке индуктивности). Используя эти графики можно рассмотреть задания, связанные с профессиональной подготовкой электриков. С помощью производной можно рассчитывать оптимальные режимы работы электротехнических устройств.
Для газоэлектросварщиков важную роль играют такие темы по геометрии, как «Площадь поверхностей тел» и «Объемы тел». В производственной практике может возникнуть задача на определение соотношения между радиусом и высотой цилиндра, при котором объем цилиндра будет наибольшим (при сварке цилиндрических емкостей). Эту задачу также рационально решать с применением производной.
Особую пользу приносит составление самими учащимися задач с производственным содержанием. Мы предлагаем составить задачи, в которых было бы показано применение математики на практике именно в их профессии. Ребята с интересом и успешно с такими творческими самостоятельными работами справляются. Лучшие из этих работ накапливаются и применяются на уроках.
Предлагаем подборку задач с профессиональной направленностью:
Для профессии «газоэлектросварщик»:
Задача 1. Открытый кузов грузового автомобиля имеет вид прямоугольного параллелепипеда с площадью поверхности S. Каковы должны быть длина и ширина кузова, чтобы его объем был наибольшим, а отношение длины к ширине равнялось 
?
Задача 2. Открытый бак, имеющий форму прямоугольного параллелепипеда с квадратным основанием, должен вмещать 13,5 л. жидкости. При каких размерах бака на его изготовление потребуется наименьшее количество оцинкованного железа?
Задача 3. Требуется сделать из листового железа цилиндрический сосуд вместимостью 
V, закрытый сверху и снизу. Каковы должны быть его размеры, чтобы затраты материала были наименьшими?
Задача 4. Для хранения строительных материалов нужно сделать временное хранилище в виде сварного каркаса, накрытого брезентом. Для изготовления каркаса, имеющего вид правильной четырехугольной призмы, имеется 36 м. металлического прута. Какую нужно выбрать длину, ширину и высоту каркаса, чтобы под навес уместилось как можно больше строительных материалов?
Задача 5. Экспериментально установлено, что расход бензина Y (л) на 100 км пути автомобиля ГАЗ-69 в зависимости от скорости X (км/ч) описывается функцией: 
Определите наиболее экономичную скорость автомобиля, при которой расход бензина будет наименьшим. Найдите это наименьшее количество бензина.
Задача 6. Скорость автомобиля изменяется по закону 
(м/сек). В какой момент времени ускорение движения будет наименьшим, если движение рассматривать за промежуток от 
c до 
с?
Задача 7. Цилиндрический бак, наполовину наполненный бензином, лежит на земле. Бак имеет две вертикальные плоские стенки, диаметр каждой из них 2 м. Определите величину давления на каждую из этих стенок бака, если плотность бензина 0,69 т/
.
Задача 8. Цилиндрическая дымовая труба с диаметром 65 см. имеет высоту 18 м. Сколько жести нужно для ее изготовления, если на заклепку уходит 10 % материала?
Задача 9. Сколько квадратных метров латунного листа потребуется, чтобы сделать рупор, у которого диаметр одного конца 0,43 м, а другого конца 0,0396 м и образующая 1,42 м.
Задача 10. Цистерна состоит из цилиндра и двух шаровых сегментов. Диаметр цистерны 1,2 м, длина цилиндрической части 3,5 м, общая длина 4 м. Сколько листовой стали пойдет на изготовление цистерны (припуск 2 % поверхности).
Задача 11. Вычислить рабочий объем цилиндра двигателя внутреннего сгорания, если диаметр равен 76 мм, и ход поршня 22 мм (
) — S-рабочий ход.
Задача 12. Два бака в форме прямоугольного параллелепипеда размером 
м
каждый наполнен один керосином, другой бензином. На сколько масса керосина в первом баке больше массы бензина во втором, если плотность керосина 0,8 кг/дм
, а бензина 0,7 кг/дм
?
Задача 13. Сколько тонн бензина можно хранить в цистерне цилиндрической формы, если ее диаметр 3 м, длина 5 м? Плотность бензина 0,7 г/см
.
Для профессии «электромонтажник»:
Задача 1. Конденсатор имеет пластины прямоугольной формы.
Периметр одной пластины равен P. При каких размерах сторон пластины емкость конденсатора будет наибольшей?
Задача 2. Железный прямоугольный сердечник трансформатора тока погружен в цилиндрическую катушку с заданным радиусом сечения. Найти размеры сторон сечения сердечника, при которых он наиболее полно заполняет внутреннюю область катушки.
Задача 3. Напряжение в цепи падает в зависимости от времени равномерно (по линейному закону). В начале опыта напряжение было 12 В, по окончанию опыта, длившегося 8 с, напряжение упало до 6,4 В. Выразить напряжение U как функцию времени t и построить график этой функции.
Задача 4. Электромонтажнику необходимо разместить десять мест для элементов схемы по окружности таким образом, чтобы расстояние между центрами было равно 25 мм. Определить необходимый диаметр окружности. (формула, выражающая сторону правильного многоугольника через радиус описанной окружности: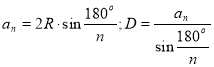 
)
Задача 5. Для обмотки трансформатора большой мощности была выбрана прямоугольная шина сечением 5 мм x 10 мм. Показать, что в этом случае трансформатор может быть больше нагружен, чем при выборе круглого провода с такой же площадью сечения
Задача 6. Шар радиусом 0,1 м имеет заряд 
кл. Определить заряд, приходящийся на единицу поверхности шара.
Задача 7. Два шара имеют одинаковый заряд, но удельный поверхностный заряд одного из шаров больше другого в 4 раза. Определить соотношение между радиусами шаров.
Задача 8. Пластины плоских конденсаторов выполнены в форме круга, квадрата и равностороннего треугольника, которые имеют одинаковый периметр P=0,1 м. Определить, какой из конденсаторов имеет наибольшую емкость, если расстояние между пластинами d=0,05 мм, а относительная диэлектрическая проницаемость 
.
— формула определения емкости плоского конденсатора.
— электрическая постоянная.
Задача 9. Определить минимальный диаметр медной проволоки длиной 100 м, если ее сопротивление не должно превышать 1 Ом.
Чему равно сопротивление 1 м медной проволоки диаметром 0,5 мм?
— сопротивление металлического проводника,
Задача 10. Рамка электроизмерительного прибора представляет собой квадрат со стороной 30 мм. На ней виток к витку намотана единая проволока диаметром 0,05 мм. Какой ширины должна быть выбрана рамка, чтобы сопротивление ее обмотки было не менее 105 Ом?
Задача 11. Исследовать условия работы источника тока, имеющего ЭДС 
и внутреннее сопротивление r. Каким должно быть сопротивление R нагрузки, чтобы получить максимальную полезную мощность?
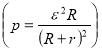
Для профессии «мастер отделочных работ»:
Задача 1. Сколько олифы потребуется для окраски внешней поверхности 100 ведер конической формы, если диаметры ведер 25 см и 30 см, образующая 27,5 см и если на 1 м требуется 150 г олифы?
Задача 2. Крыша имеет форму конуса. Высота крыши 2 м, диаметр 6 м. Сколько краски потребуется на ее окраску, если на 1 м требуется 80 г краски?
Задача 3. Воронка вентиляционной трубы имеет форму правильной четырехугольной усеченной пирамиды со сторонами оснований 120 см и 50 см и расстояниями между основаниями 60 см. Сколько краски понадобится для покраски воронки внутри и снаружи, если на 1 м поверхности требуется 0,25 кг краски?
Задача 4. Цилиндрическая дымовая труба с диаметром 0,65 см имеет высоту 18 м. Сколько краски требуется на ее покрытие, если на 1 м расходуется 100 г краски?
Задача 5. Из каких правильных многоугольников можно выложить паркет?
Задача 6. На сколько увеличится стоимость штукатурки в помещении размером 2,75x2,5x4 м, если толщину штукатурки увеличить на 2 мм. Стоимость 1 м раствора — x руб.
Задача 7. Найти массу песка, пригодного для мозаичных работ, если он ссыпан в кучу, имеющую форму конуса диаметром 3 м и высотой 1,4 м. Объемная масса песка 1700 кг/м, влажность песка 8 %, а при такой влажности его объем надо уменьшить на 15 %.
Задача 8. Требуется оштукатурить две колонны одинаковой высоты: круглого сечения с диаметром 30 см и квадратного сечения со стороной 30 см. На оштукатуривание какой колонны пойдет больше материала и во сколько раз?
Задача 9. При оштукатуривании вручную колонны рабочему потребуется 4 часа. Какую площадь поверхности он оштукатуривает за 1 час, если высота колонны 7 м, диаметр основания 0,8 м?
Задача 10. Сколько времени потребуется рабочему, чтобы оштукатурить колонну высотой 6 м, диаметром 1 м, соблюдая норму времени 0,79 часа на 1 м?
Задача 11. Для облицовки пола имеются плитки основного тона и фризовые, причем плиток основного тона больше. При укладке фризовых плиток в форму прямоугольника, его периметр будет равен 10 м. Какими по размеру должны быть стороны прямоугольника, чтобы имеющимся количеством фризовой плитки ограничить наибольшую поверхность?
Задача 12. Башня квадратного сечения имеет пирамидальную крышу, высота которой равна h(м). Определить площадь крыши, если сторона квадрата равна а(м). Сколько краски потребуется на ее покраску, если на 1 м расходуется b(г) краски.
Задача 13. Крыша башни имеет вид правильной шестиугольной пирамиды.
Сторона основания равна 1,8 м. Высота 12 м. Сколько краски пойдет на покраску крыши, если на 1 м расходуется 200 г краски.
Задача 14. Сколько краски потребуется для покраски в два слоя поверхности цилиндрической трубы длиной 1,43 м, если внешний ее диаметр равен 0,94 м, а толщина стенок 0,07 м, а на покраску 1 м требуется 150 г краски.
Литература:
- И. И. Чичерин. «Общестроительные работы». Москва 1999. Издательский центр «Академия».
- Н. П. Гужов; В. Я. Ольховский. «Системы электроснабжения». Ростов-на-Дону. 2011.
- А. А. Ивлев; А. А. Кальгин. «Отделочные строительные работы». Москва 1999. Издательский центр «Академия».
