Пусть ![]() множество комплексных чисел,
множество комплексных чисел, ![]() - декартовое произведение, а
- декартовое произведение, а ![]() множество матриц размера
множество матриц размера ![]() с комплексными элементами.
с комплексными элементами.
Если для матрицы ![]() имеет место неравенство
имеет место неравенство ![]() при всех
при всех ![]() , то матрица
, то матрица ![]() называется положительно определенным. Если выполняется условие
называется положительно определенным. Если выполняется условие ![]() при всех ненулевых
при всех ненулевых ![]() , то матрица
, то матрица ![]() называется строго положительно определенным.
называется строго положительно определенным.
Если матрица ![]() является положительной, то говорят, что
является положительной, то говорят, что ![]() .
.
Если при всех ![]() выполняется равенство
выполняется равенство ![]() , то матрица
, то матрица ![]() называется эрмитовой или самосопряженной.
называется эрмитовой или самосопряженной.
Приведем некоторые факты о положительно определенных матриц.
Предложение 1. Матрица ![]() является положительной тогда и только тогда, когда она эрмитова и ее все собственные значения неотрицательны. Матрица
является положительной тогда и только тогда, когда она эрмитова и ее все собственные значения неотрицательны. Матрица ![]() является строго положительной тогда и только тогда, когда она эрмитова и ее все собственные значения положительны.
является строго положительной тогда и только тогда, когда она эрмитова и ее все собственные значения положительны.
Предложение 2. Матрица ![]() является положительной тогда и только тогда, когда она эрмитова и ее главные миноры неотрицательные. Матрица
является положительной тогда и только тогда, когда она эрмитова и ее главные миноры неотрицательные. Матрица ![]() является строго положительной тогда и только тогда, когда она эрмитова и ее все главные миноры положительные.
является строго положительной тогда и только тогда, когда она эрмитова и ее все главные миноры положительные.
Предложение 3. Матрица ![]() является положительной тогда и только тогда, когда существует матрица
является положительной тогда и только тогда, когда существует матрица ![]() такая, что
такая, что ![]() . Матрица
. Матрица ![]() является строго положительной тогда и только тогда, когда матрица
является строго положительной тогда и только тогда, когда матрица ![]() не сингулярная.
не сингулярная.
Предложение 4. Матрица ![]() является положительной тогда и только тогда, когда существует положительная матрица
является положительной тогда и только тогда, когда существует положительная матрица ![]() такая, что
такая, что ![]() . Матрица
. Матрица ![]() является строго положительной тогда и только тогда, когда матрица
является строго положительной тогда и только тогда, когда матрица ![]() строго положительна.
строго положительна.
Заметим, что в Предложение 4, матрица является единственной, и она называется квадратным корнем матрицы ![]() и обозначается через
и обозначается через ![]() .
.
Пусть
Теорема 1. Матрица ![]() является положительной тогда и только тогда, когда существуют элементы
является положительной тогда и только тогда, когда существуют элементы ![]() такие, что,
такие, что,
![]() .
.
Матрица ![]() является строго положительной тогда и только тогда, когда элементы
является строго положительной тогда и только тогда, когда элементы ![]() ,
, ![]() линейно независимы.
линейно независимы.
Рассмотрим пример на применении теоремы 1.
Пример 1. Пусть ![]() фиксированные вещественные положительные числа. Определим матрицу
фиксированные вещественные положительные числа. Определим матрицу ![]() размера
размера ![]() с элементами
с элементами
![]() .
.
Такая матрица называется матрицей Коши. Тогда имеет место соотношение
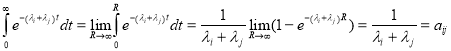 .
.
Если ![]() ,
, ![]() , то
, то ![]() и при всех
и при всех ![]() имеет место равенство
имеет место равенство ![]() , где для элементов
, где для элементов ![]() справедливо равенство
справедливо равенство
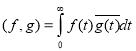 .
.
В силу теоремы 1 матрица
Если ![]() и
и ![]() положительные эрмитовы матрицы, то
положительные эрмитовы матрицы, то ![]() также положительная эрмитова матрица. Произведение матриц
также положительная эрмитова матрица. Произведение матриц ![]() является эрмитовым тогда и только тогда, когда
является эрмитовым тогда и только тогда, когда ![]() и
и ![]() коммутативные матрицы.
коммутативные матрицы.
Матрица ![]() называется симметрическим произведением матриц
называется симметрическим произведением матриц ![]() и
и ![]() . Если матрицы
. Если матрицы ![]() и
и ![]() эрмитовы, то
эрмитовы, то ![]() также эрмитова. Вообще говоря, из положительности матриц
также эрмитова. Вообще говоря, из положительности матриц ![]() и
и ![]() не всегда вытекает положительность матрицы
не всегда вытекает положительность матрицы ![]() .
.
Пример 2. Для любых ![]() определим эрмитовы матрицы
определим эрмитовы матрицы
![]() ,
, ![]() .
.
Видно, что если ![]() , то матрица
, то матрица ![]() является положительно определенной. Для любого элемента
является положительно определенной. Для любого элемента ![]() имеет место равенство
имеет место равенство
![]() .
.
Через ![]() обозначим аргумент комплексного числа
обозначим аргумент комплексного числа ![]() . Тогда имеет место равенство
. Тогда имеет место равенство ![]() . Поэтому квадратичная форма
. Поэтому квадратичная форма ![]() записывается в виде
записывается в виде ![]() . Таким образом, при
. Таким образом, при ![]() матрица
матрица ![]() является положительно определенной. По определению
является положительно определенной. По определению ![]() имеет место равенство
имеет место равенство
![]() ,
,
следовательно, для любого элемента ![]() имеет место равенство
имеет место равенство
![]() .
.
При этом, если
Пусть ![]() и
и ![]() эрмитовы матрицы и матрица
эрмитовы матрицы и матрица ![]() строго положительна. Если симметрическое произведение
строго положительна. Если симметрическое произведение ![]() является положительным (строго положительным), то матрица
является положительным (строго положительным), то матрица ![]() также является положительным (строго положительным).
также является положительным (строго положительным).
Литература:
- R. Bhatia. Matrix analysis. Springer-Verlag, New York, 1997.
- R. Bhatia. Positive definite matrices. In: Princeton Series in Applied Mathematics. Princeton University Press, 1997.







