Обобщеннaя формула Дюпюи



В статье предложена более общая формула, подобная формуле Дюпюи, которая учитывает также влияние начального градиента и инерционных сил.

Ключевые слова: скорость, инерционные силы, начальный градиент

In this article more general formula is proposed. It is similar to the Dupee formula, which also takes into account the influence of the initial gradient and inertial forces.

Keywords: speed, inertial forces, initial gradient

Основной задачей рациональной разработки нефтяных и газовых месторождений является полнота извлечения промышленных запасов нефтей.

При разработке залежей с аномальными свойствами нефтей возникает ряд сложных и специфических задач, связанных с изучением физических и гидродинамических основ проявления неньютоновского характера фильтрации в пористой среде.

Анализ индикаторных линий, снятых при фильтрации однофазной нефти, указывает на структурно-механические свойства нефтей. На оси индикаторных линий отсекается отрезок который идет на преодоление начального градиента давления.

Существуют различные факторы, влияющие на начальный градиент 1–5.

Приведенные факты показывают, что многие жидкости (нефть, пластовая вода), не проявляющие аномальных свойств вне контакта с пористой средой, при малых скоростях фильтрации, могут образовывать неньютоновские системы, взаимодействуя с пористой породой. Наличие начального градиента давления , при достижении которого начинается фильтрация, было обнаружено и при движении флюидов в газонасыщенных пористых средах.

При этом было установлено, что изменяется в широких пределах и в большинстве случаев тем выше, чем больше глинистого материала содержится в пористой среде и чем выше остаточная водонасыщенность газоводяной смеси.

Наряду с этим неньютоновские свойства пластовых нефтей с повышенным содержанием высокомолекулярных компонентов (смол, асфальтенов, парафина и т. д.) могут проявляться в широком диапазоне изменения скоростей.

Таким образом, при малых скоростях течения природа нелинейности закона фильтрации иная, чем в области больших скоростей фильтрации.

Следует также отметить, что наличие у жидкости релаксационных (неравновесных) свойств определяет характер сопротивления при движении в пористой среде. Течение через сужения и расширения поровых каналов сопровождается деформацией жидких частиц. Поскольку релаксирующая жидкость реагирует на изменение условий с некоторым запаздыванием, то в зависимости от скорости движения характер сопротивления будет меняться. Когда течение достаточно медленное, соответственно медленно происходят деформации жидких частиц, и жидкость успевает реагировать на эти изменения. С увеличением скорости движения время прохождения через сужение уменьшается, и жидкие частицы не успевают деформироваться. Это приводит к увеличению сопротивления движения 3.

Следовательно, проведенные исследования показывают, что наличие начального градиента имеет место не только на нефтяных, но и на газовых месторождениях. Кроме того, начальный градиент в основном не остается неизменным в процессе разработки, а часто изменяется. Он может как исчезать, так и возрастать во времени.

В работе делается попытка обобщения закона фильтрации при учете влияния начального градиента и инерционных сил при фильтрации нефти с аномальными свойствами в пористой среде.

В наиболее общем случае закон фильтрации можно представить следующим образом:

(1)

Здесь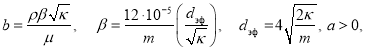

Следует отметить, что все процессы, которые искривляют диаграмму, увеличивают коэффициенты а, b и наоборот.

Как известно, в 1901 г. Форхгеймер, ссылаясь на исследования Мазони, рекомендовал выражать зависимость градиента давления от скорости (при больших градиентах) формулой:

где а и b — эмпирические коэффициенты. Будем считать это выражение моделью 1. Однако ученый отметил, что еще лучше зависимость от u будет выражаться трехчленным законом (модель 2):

где с — эмпирический коэффициент.

Для проверки этого положения были обработаны индикаторные диаграммы некоторых скважин Уренгойского месторождения. Результаты обработки показали, что для прогноза модель 2 дает результаты значительно точнее, чем модель 1.

Таким образом, использование кубического слагаемого в уравнении связано с необходимостью увеличения точности. Однако это необходимо также и для учета неравновесных свойств фильтрационного потока и влияния инерционных сил. Как видно, при из формулы (1) получается закон Дарси. При получается двучленный закон Форхгеймера. А при получается общий закон фильтрации Мирзаджанзаде. Подставляя в уравнение (1) получаем:

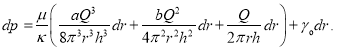
Интегрируя левую часть этого равенства от , а правую часть от , получаем:

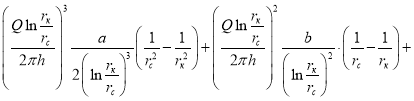
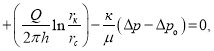
где .(2)

Сделав подстановки ,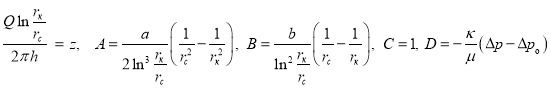

мы получаем кубическое уравнение в виде Для решения этого кубического уравнения используем подстановку Тогда данное кубическое уравнение представится в виде:

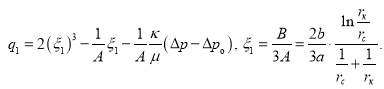
Для поставленной задачи и данное уравнение имеет всего один действительный корень, который можно найти по формуле Кардано.

Решение уравнения (1) по формуле Кардано имеет вид:

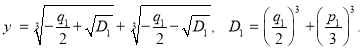
Последнее можно преобразовать в следующий вид:

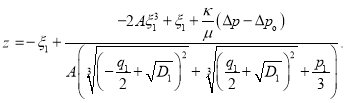
Делая подстановку 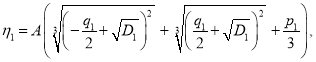мы получаем:

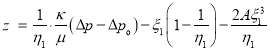.(3)

Здесь — безразмерный параметр, величина которого приблизительно равна единице Однако она — переменная величина. Учитывая в (3) 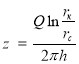, мы получаем:

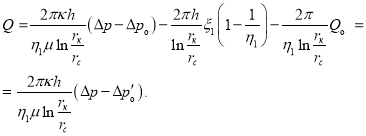(4)

Здесь (5)

Учитывая, что то из формулы (4) получается формула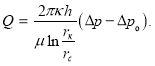

Как видно из (5), градиент давления, который направлен против движения состоит из трех составляющих. Первая — это начальное пластовое давление вторая – и третья —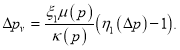

Первая составляющая в основном связана со свойствами флюида, пористой среды и их взаимодействием на призабойной зоне. Вторая составляющая связана с коэффициентами а, b, характером изменения в процессе разработки 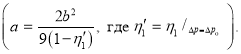А третья составляющая учитывает влияние инерционных сил.

Графики изменения схематично имеют следующий вид:

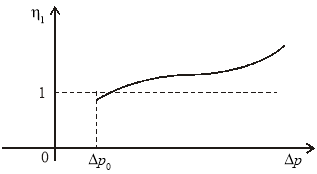
Рис. 1.

График изменения параметра от депрессии

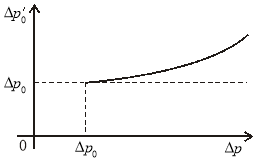
Рис. 2.

График изменения от депрессии

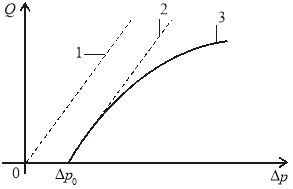
Рис. 3.

График изменения Q от

1 — по формуле Дюпюи; 2 — по формуле 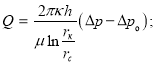3 — по формуле

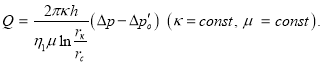
Эта задача актуальна, потому что увеличение градиента, направленное против движения, отрицательно влияет на количество извлекаемых запасов. Со временем актуальность этой задачи будет увеличиваться в связи с тем, что открываемые новые месторождения находятся на все более больших глубинах. А с увеличением глубины увеличивается и скорость, и градиент давления. Поэтому увеличиваются и сопротивления, связанные с влиянием инерционных сил.

Таким образом, в статье получена более общая формула, учитывающая начальный градиент и влияние инерционных сил. В связи с этим ее можно назвать обобщенной формулой Дюпюи.

Литература:

1. А. Х. Мирзаджанзаде, О. Л. Кузнецов, Х. С. Басниев, З. С. Алиев. Основа технологии добычи газа. — М.: Недра, 2003, 880 с.
2. А. Х. Мирзаджанзаде, И. М. Аметов, А. Г. Ковалев. Физика нефтяного и газового пласта. — Москва-Ижевск: Институт компьютерных исследований, 2005, 280 с.
3. А. Х. Мирзаджанзаде, А. Г. Ковалев, Ю. В. Зайцев. Особенности эксплуатации месторождений аномальных нефтей. –М.: Недра, 1972, с.200.
4. А. Х. Мирзаджанзаде, Р. С. Гурбанов. Обзор работ по гидродинамике вязкопластичных сред в бурении. — Баку: 1968, 83 с.
5. А. Т. Горбунов. Разработка аномальных месторождений. — М.: Недра, 1981, 240 с.