Статья посвящена использованию регрессионного анализа для возможности проведения прогнозирования уровня электромагнитного поля в системах подвижной радиосвязи с помощью математического моделирования. Это позволит автоматизировать процесс стабилизации параметров качества сети посредством управления уровнем электромагнитного поля в системах мобильной связи.
Ключевые слова: уровень электромагнитного поля, математическая модель, прогнозирование
До настоящего времени процесс автоматизации контроля за уровнем электромагнитного поля в системах мобильной связи не признан актуальным лишь по причине отсутствия возможности такового контроля. В свете современных научных разработок [1–4] нацеленных на повышение качества самоконтроля систем сотовой связи через увеличение «линий обратной связи» системы в целом, задачей которых является расширение перечня контролируемых параметров сети для повышения степени её устойчивости и, как результат повышения качества предоставляемых услуг в системах беспроводного доступа. Способы мониторинга рассмотрены в работах [1, 4].
Для удалённого мониторинга предлагается установка сенсорных датчиков в зонах обслуживания каждого из секторов базовых станций (БС), которые должны измерять и передавать данные об уровне электромагнитного поля (ЭМП), образуемого антенными системами сотовой связи на центральный контроллер БС по каналам передачи данных или линиям сигнализации системы мобильной связи. Контроллер системы сотовой связи, как система, предназначенная для управления процессами соединения абонентов, одновременно оценивает качество соединений и принимает управляющие решения о переключении каналов с целью предоставления услуг с максимальным качеством. Система также контролирует уровни мощности базовых станций.
Регрессионный анализ — способ моделирования измеряемых данных и исследования их параметров. Основная цель регрессионного анализа состоит в определении связи между некоторой характеристикой Y наблюдаемого явления или объекта и величинами х1, х2, …, хn, которые обусловливают, объясняют изменения Y. Переменная Y называется зависимой переменной (откликом), влияющие переменные х1, х2, …, хn называются факторами (регрессорами). Установление формы зависимости, подбор модели (уравнения) регрессии и оценка её параметров являются задачами регрессионного анализа [7, с. 3].
Допустим, что измеряемые значения будут представлены в виде таблицы (табл.1), измерения сделаны одним датчиком в одном секторе зоны действия базовой станции за период времени ti равным каждым 10 секундам.
Таблица 1
Фрагмент значений мониторинга уровня электромагнитного поля для одного датчика
|
Сетевой номер датчика |
Время, ti, сек |
Уровень электромагнитного поля L, дБ |
|
XX-UUU-1–1 |
10 |
-62 |
|
20 |
-65 |
|
|
30 |
-69 |
|
|
40 |
-67 |
|
|
50 |
-71 |
|
|
60 |
-76 |
|
|
70 |
-80 |
|
|
80 |
-77 |
|
|
90 |
-82 |
|
|
100 |
-85 |
|
|
110 |
-89 |
|
|
120 |
-92 |
Проведём регрессионный анализ и прогнозирование измеряемых значений. Для проведения регрессионного анализа и прогнозирования необходимо построить график исходных данных и попытаться приближённо определить характер зависимости (рис. 1) и выбрать вид функции регрессии, которая может описывать связь исходных данных.
Поскольку исследуется связь между двумя признаками, регрессия будет являться парной. По рисунку 1 видно, что вид функции регрессии вероятнее всего будет линейным.
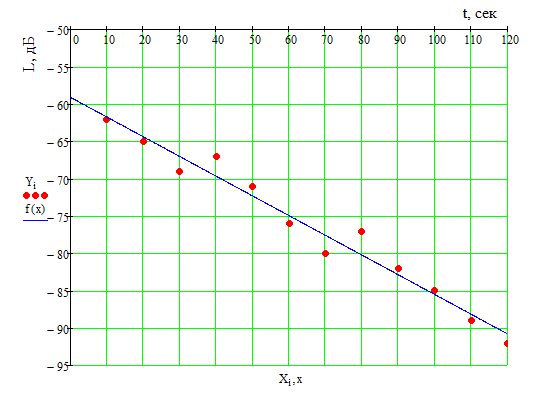
Рис. 1. График измерений, сделанных одним датчиком в одном секторе зоны действия базовой станции за период времени ti равным каждым 10 секундам
Уравнение линейной парной регрессии выглядит следующим образом [6, с. 11]:
![]() (1)
(1)
где [6, с. 12]:
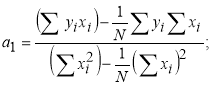 (2)
(2)
![]() (3)
(3)
При помощи этого уравнения переменная y выражается через константу a0 и угол наклона прямой (или угловой коэффициент) а1, умноженный на значение переменной x. Константу a0 также называют свободным членом, а угловой коэффициент — коэффициентом регрессии.
Вычислим коэффициенты линейной регрессии по формулам (2) и (3):
![]()
Таким образом, искомая регрессионная зависимость имеет вид:
![]()
где y(x) это спрогнозированные значения уровня (L, дБ) электромагнитного поля за время (t, сек) измерения x. Определяем направление связи между переменными: знак коэффициента регрессии отрицательный, следовательно, связь также является отрицательной, что подтверждает графическое предположение (рис. 1).
Найденная функция y(x) и будет являться математической моделью данного процесса. С её помощью можно будет прогнозировать вероятные аварии, сбои и ошибки.
Для анализа общего качества уравнения регрессии используют коэффициент детерминации R2, называемый также квадратом коэффициента множественной корреляции. Коэффициент детерминации (мера определённости) всегда находится в пределах интервала [0;1]. Если значение R2 близко к единице, это означает, что построенная модель объясняет почти всю изменчивость соответствующих переменных. И наоборот, значение R2 близкое к нулю, означает плохое качество построенной модели [6, с. 13].
Вычислим коэффициент детерминации по формуле (4):
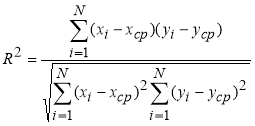 (4)
(4)
где [6, с.13]:
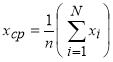 ,(5)
,(5)
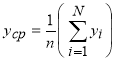 .(6)
.(6)
Тогда: R2=0,98 или 98 %
Таким образом, коэффициент детерминации показывает, что построенная линейная модель объясняет почти изменчивость соответствующих переменных и подтверждает их тесную связь, тем самым доказывая, что данная модель имеет место быть.
Оценка значимости уравнения регрессии осуществляется с помощью критерия Фишера (см. формулу 7) [7, с. 4]. При условии справедливости нулевой гипотезы (R2=0) критерий имеет распределение Фишера с числом степеней свободы k1=p, k2 =n-p-1 (для парной линейной регрессии р = 1). Если нулевая гипотеза отклоняется, как в нашем случае то уравнение регрессии считается статистически значимым. Если нулевая гипотеза не отклоняется, то признается статистическая незначимость или ненадёжность уравнения регрессии [7, с. 4].
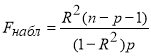 (7)
(7)
Fнабл=242,52
Полученное значение сравнивается с критическим значением из специальной таблицы Значения F-распределения Фишера (для уровня значимости P=0,05). Для степеней свободы k1=1 и k2 =10 значение Fкр=4,96. Т. к. Fнабл=242,52> Fкр=4,96 можно сделать вывод, что уравнение регрессии статистически значимо.
При таком высоком значении коэффициента детерминации и успешной проверке адекватности модели по критерию Фишера, можно делать прогноз о предполагаемом значении уровня электромагнитного поля в определённый промежуток времени измерений.
Вывод.
Проведённые исследования показали возможность автоматизированного управления контролем уровня электромагнитного поля (ЭМП) в системах подвижной радиосвязи, что позволит устанавливать, контролировать и удерживать в максимально стабильном состоянии и другие наиболее критичные параметры (не только ЭМП), влияющие на уровень качества предоставляемых услуг в системах беспроводного доступа.
Литература:
- Пищин О. Н., Хаирова А. Р. Система обратной связи контроля уровня электромагнитного поля на узлах подвижной радиосвязи. Научные тенденции: Вопросы точных наук. Сборник научных трудов по материалам международной научной конференции 12 декабря 2016г. Изд-во ЦНК МНИФ «Общественная наука», 2016. С. 10–16.
- Пищин О. Н., Джамалидинова М. Е. Контроль управления качеством системы управления на основе интеллектуальной системы поддержки принятия решений «Наука, образование, инновации: пути развития». Материалы седьмой всероссийской научно-практ. конф. (24–26 мая 2016 г.) г. Петропавловск-Камчатский: КамчатГТУ, 2016, С. 36–41.
- Пищин О. Н., Залесская Л. В., Покусаев М. А. Модель стабилизации качества параметров систем подвижной радиосвязи. Материалы I международной научной конференции: «Наука в современном мире» 22–23 мая 2015 г. Научно-информационный издательский центр и редакция журнала «Актуальные проблемы гуманитарных и естественных наук» № 6–4–2015, С. 19–22.
- О. Н. Пищин. Альтернативные сети сигнализации и контроля функциональности систем подвижной радиосвязи. Вестник Астраханского государственного технического университета. Серия: Управление, вычислительная техника и информатика. Выпуск 2 — Астрахань: Изд-во АГТУ, 2010. — с. 135–140.
- А. Н. Мелихов, Л. С. Бернштейн, С. Я. Коровин. Ситуационные советующие системы с нечёткой логикой. М.: Наука, 1990. — 272 с.
- Использование регрессионного анализа для исследования процессов управления сложными системами: Метод. указания / СГАУ. Сост. А. Б. Прокофьев, Е. В. Шахматов. — Самара, СГАУ, 2005. — 23 с.
- Интернет ресурс: Парная линейная регрессионная модель // Лекции. Орг — публикация материала для обучения. URL: http://lektsii.org/15–50232.html (дата обращения: 7.04.2017 г.).







