Пусть 
— комплексное гильбертово пространство и 
линейный оператор с областью определения 
. Множество
называется числовым образом оператора 
Из определения видно, что множество 
является подмножеством комплексной плоскости и геометрические свойства множества 
дает некоторые информации об операторе 
.
Изучение числового образа линейного оператора в гильбертовом пространстве является одним из основных методов в изучении местоположения спектра таких операторов. Это понятие впервые введено в работе [1]. Вслед за этим это понятие обобщено разными способами, см. например [2–4].
Пусть 
- 
-мерный тор с условием 
и 
— гильбертово пространство квадратично интегрируемых (комплекснозначных) функций, определенных на 
. Обозначим через прямую сумму пространств 
и 
, т. е. 
.
Рассмотрим обобщенную модель Фридрихса 
действующую в гильбертовом пространстве 
как 
блочно-операторная матрица
,
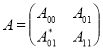где матричные элементы 
, определяются по формулам
, 
Здесь 
, 
, 
и 
вещественнозначные непрерывные функции на 
, а 
сопряженный оператор к 
. Оператор называется оператором уничтожения, а называется оператором рождения.
При этих предположениях операторная матрица 
, является ограниченным и самосопряженным в гильбертовом пространстве 
.
Можно показать, что для существенного спектра оператора 
имеет место равенство 
, где числа 
и 
определяются следующим образом: 
, 
.
Определим регулярную в 
функцию (детерминант Фредгольма, ассоциированный с оператором A)
.
Тогда оператор имеет собственное значение 
тогда и только тогда, когда 
. Далее, в случае существовании собственных значений оператора 
обозначим их через 
, 
. Для определенности предположим, что 
и 
.
Пусть 
−фиксированное натуральное число. На протяжении всей работы будем предполагать, что функция 
имеет невырожденный минимум в точках 
, 
.
Пусть
, 
, 
.
Так как функция 
имеет невырожденный минимум в точках 
, 
, существуют числа 
, 
, 
и 
такие, что
, 
, 
; (1)
, 
. (2)
Имеет место равенство
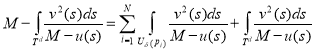(3)
Учитывая неравенства (1) и непрерывность функции 
на 
имеем, что 
- тое (
) слагаемое в правой части (3) оценивается следующим образом:
.
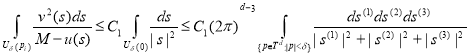Переходя в сферическую систему координат убедимся, что последний интеграл конечна. 
конечность последнего слагаемого в правой части (3), т. е. интеграл по 
вытекает из непрерывности функции 
на 
и неравенства (2).
Положим
.
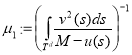Следующая теорема описывает структуру числового образа оператора 
.
Теорема. Пусть 
.
1) Если
, то верно равенство 
.
2) При 
имеет место равенство 
.
Литература:
- O. Toeplitz. Das algebraische Analogon zu einem Satze von Fejer. Math. Z., 2:1–2 (1918), 187–197.
- H. Langer, A. S. Markus, V. I. Matsaev, C. Tretter. A new concept for block operator matrices: the quadratic numerical range. Linear Algebra Appl., 330:1–3 (2001), 89–112.
- L. Rodman, I. M. Spitkovsky. Ratio numerical ranges of operators. Integr. Equ. Oper. Theory, 71 (2011), 245–257.
- M. T. Heydari. Numerical range and compact convex sets. Rend. Circ. Mat. Palermo, 60 (2011), 139–143.
