Евклидова плоскость в четырехмерном пространстве



Определение.Поверхности и называются изометричными, если существует одно-однозначное отображение поверхности на поверхность , при котором соответствующие кривые на этих поверхностях имеют одинаковые длины [1].

Пусть -регулярное поверхность, -какая-нибудь ее регулярная параметризация.

В теории поверхностей важную роль играют первая квадратичная форма, связанные с поверхностью:

Перваяквадратичная форма является положительно определенной, так как она принимает только неотрицательные значения и обращается в нуль только при . Коротко слова,

где , , [4].

Теорема [1]. Если регулярные поверхности и можно параметризовать так, что их первые квадратичные формы будут одинаковы, то поверхности изометричны. Изометрическое отображение заключается в сопоставлении точек с одинаковыми координатами.

Обратно, если поверхности и изометричны, то они могут быть параметризованы, так что их первые квадратичные формы будут одинаковы

Поверхность, представляющая собой геометрическое место прямых линий, называется линейчатой [2].

Все поверхности пространства , изометричные евклидовой плоскости, простираются в бесконечность, так как они необходимо должны быть линейчатыми поверхностями. Напротив, в пространстве существует поверности, изометричные плоскости в малом и не являющиеся линейчатыми поверхностями. Дадим пример подобной поверхности ; она целиком расположена в конечной области и топологически эквивалентна поверхности тора. Это поверхность представляется в параметрической форме очен просто:

Линейный элемент поверхности есть

Таким образом поверхность в самом деле изометрична плоскости с прямоугольными координатами . Эта поверхность целиком расположена в конечной области, так как все координаты лежат между -1 и +1. Впрочем можно представить поверхность как сечение двух трехмерных гиперцилиндров

и .

Все точки поверхности можно получить, если застамить в декартовой плоскости координат пробегать все точки квадрата со сторонами, параллельными осям и имеющими длина . Различным внутренним точкам квадрата соответствуют различные точки поверхности .Наоборот две граничныеточки квадрата представляют одну и ту же точку поверхности , если они расположены но одной и той же прямой и на противоположных сторонах квадрата. Следовательна, есть поверхность тора, а -плоскость есть универсальная поверхность наложения для поверхности .

Можно было бы попытаться осуществить евклидову геометрию на замкнутых поверхностях, не имеющих вида тора. Оказывается, однако, что для этого можно взять только бутылку Клейна. Но на замкнутых поверхностях со связностью и только на них можно осуществить гиперболическую геометрию. Эллиптическая геометрия не может быть осуществлена ни на какой замкнутой поверхности, кроме шара и проективной плоскости. Эти теоремы можно вывести из дифференциально-геометрической формулы Бонне относительно полной кривизны [3].

Существует ещё поверхностьизометрично евклидовой плоскости но неявляется линейчатым поверхностям, параметрической формы

(1)

Линейный элемент поверхности есть

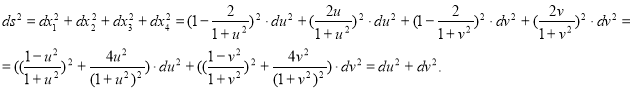
Литература:

1. А. В. Погорелов Дифференциальная геометрия Изд: «наука» Москва 1974
2. П. К. Рашевский, Курс дифференциальной геометрии. Москва 1950
3. Д.Гильберт, С.Кон-Фоссен, Наглядная геометрия,Москва “Наука” 1981
4. Артыкбаев А., Соколов Д. Д. Геометрия в целом в целом в плоском пространстве-времени. Ташкент. Изд. «Фан» 1991
5. С. Б. Кадомцев, исследование некоторых свойств нормального кручения двумерной поверхности в четырехмерном пространстве. «Проблемы геометрии» 1975,7,267–278.