Согласно статистике базы данных Web Of Science за последние 10 лет сфера киберфизических систем приобретает все большую популярность (Рис. 1).
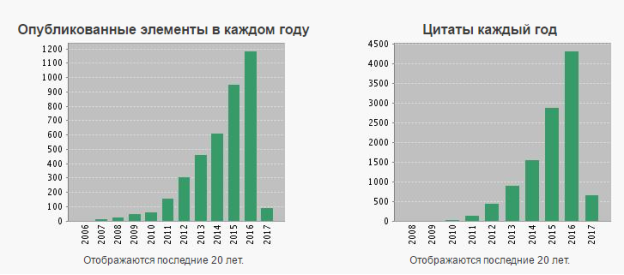
Рис. 1. Отчет по цитированию базы данных Web Of Science по запросу «cyber-physical system» за период 2006–2017 гг.
Большинство источников определяют киберфизическую систему как систему, обладающими неразрывной связью между входящими в них вычислительными и физическими элементами [1].
Однако в данной статье будем рассматривать направление из выделенного класса задач, включающих человека в контуре управления [2]. Конкретно системы захвата движений. При этом фокус внимания будет на постобработке данных, а не на областях применения.
Существует два принципиальных способа для оцифровки движений: маркерный и безмаркерный. Маркерный предполагает наличие специальных датчиков. В нашем случае это трехосевые гироскопов и акселерометры. Безмаркерные способы основаны на компьютерном зрении и распознавании образов.
Постобработка данных методов разительно отличается. Далее будем рассматривать только случай для маркерных систем.
Параметры ориентации, которые определяют гироскоп акселерометры, на практике оказываются сильно зашумленными, что создает серьезные проблемы для получения точных данных. Поэтому существует проблема — необходимость адаптации существующих алгоритмов постобработки сырых данных от плат, совмещающих трехосевые гироскопы и акселерометры. Адаптация алгоритма для постобработки данных, полученных с датчиков, позволит подготовить данные для различных real-time system.
Для сравнения качества постобработки возьмем два фильтра: Калмана и Комплементарный.
Фильтр Калмана.
Используетсявзадачах определения параметров ориентациикак динамической системы,используется уравнение
![]() ,(1)
,(1)
где ![]() – вектор состояния динамической системы;
– вектор состояния динамической системы; ![]() , k – переходная матрица состояния системы;
, k – переходная матрица состояния системы; ![]() – вектор возмущения;
– вектор возмущения;![]() , k – матрица возмущения.
, k – матрица возмущения.
Сигнал на выходе измерительной системы описывается выражением
![]() ,(2)
,(2)
где Zk – вектор измерения; Hk – матрица измерения; νk – вектор ошибки измерения.
Считается, что возмущающая последовательность wk является гауссовской белой последовательностью с нулевым средним:
M[![]() ]=0(3)
]=0(3)
и корреляционной матрицей:
M[![]() ]=
]=![]() .(4)
.(4)
Последовательность ошибок измерения νk представляет собой гауссовскую белую последовательность, для которой
M[
и M[![]() ]=
]=![]() .(6)
.(6)
Случайные процессы ![]() и
и ![]() независимы, так что:
независимы, так что:
![]() (7)
(7)
Оптимальная текущая оценка фильтра Калмана описывается соотношением:
![]() (8)
(8)
где ![]() – матрица передачи фильтра. Матрица
– матрица передачи фильтра. Матрица ![]() определяется соотношениями:
определяется соотношениями:
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
где E – единичная матрица, ![]() ,k – априорная корреляционная матрица ошибок оценивания,
,k – априорная корреляционная матрица ошибок оценивания, ![]() ,k+1 – апостериорная корреляционная матрица ошибок оценивания.
,k+1 – апостериорная корреляционная матрица ошибок оценивания.
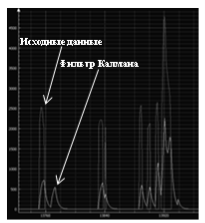
Рис. 2. Фильтр Калмана для единичных
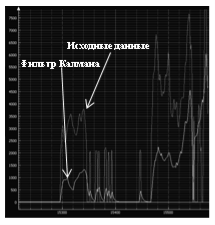
Рис. 3. Фильтр Калмана для группы пиковых значений, различных значений
Комплементарный фильтр.
Применяется для определения угла наклона. Также данный фильтр опирается на показания акселерометра и гироскопа. Ниже приведем формулу для вычисления этого угла:
![]()
где K — коэффициент фильтра (значение находятся в диапазоне от 0 до 1), φ [i],φ [i+1] — угол, вычисленный при помощи фильтра, на текущем и предыдущем шагах.
Приведем выражение для вычисления угла отклонения:
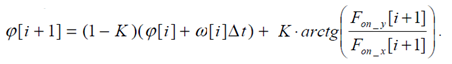
Данный фильтр является сокращенным вариантом фильтра Калмана для одномерного случая, где первое слагаемое являет собой звено предсказания. В данном случае приращение угла определяется исходя из угловой скорости на предыдущем этапе, которая измеряется непосредственно гироскопом.
При этом коэффициент K является определенной величиной. Все эти факты значительным образом упрощают вычислительный процесс, при этом значение угла можно принять достаточно точным приближением к реальному.
Отметим, что использование гироскопа рационально еще и тем, что на его выходе получается величина угловой скорости, тем самым отпадает необходимость дифференцировать величину угла, которая в свою очередь имеет высокочастотную составляющую.
Крайне важным является тот факт, что на его показания не влияют линейные ускорения. Поэтому и при объединении алгоритма управления желательно, чтобы переменные состояния измерялись датчиками, а не просто рассчитывались, при помощи значений других связующих величин. А это в свою очередь должным образом окажет положительное влияние на запас устойчивости, а также качество регулирования.
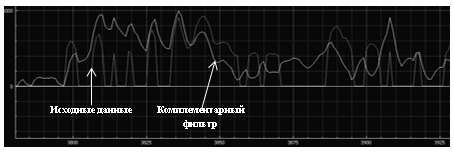
Рис. 4. Пример работы комплементарного фильтра
Сравнение фильтра Калмана и комплементарного фильтра.
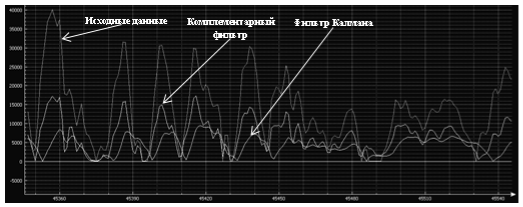
Рис. 5. Сравнение фильтров
Результаты.
Переходной процесс в выходном сигнале фильтра Калмана короче, чем в комплементарном фильтре. Кроме того, ошибка фильтрации для первого значительно меньше, чем для второго. То есть установившиеся значения выходных сигналов для фильтра Калмана гораздо ближе к истинным значениям ωx, ωy, ωz. Можно утверждать, что фильтр Калмана позволяет производить более эффективную фильтрацию сильно зашумленных сигналов.
Литература:
- //. URL: http://www.tu32.ru/article3-Киберфизические-системы (дата обращения: 15.04.2017).
- Schirner G. et al. The future of human-in-the-loop cyber-physical systems //Computer. — 2013. — Т. 46. — №. 1. — С. 36–45.
- Madgwick S. An efficient orientation filter for inertial and inertial/magnetic sensor arrays // Bristol (UK), 2010.
- Kalman R. E. A new approach to linear filtering and prediction problems // Journal of Basic Engineering.1960, N82. P. 35–45.







