В чистой математике живет всегда художник, архитектор и даже поэт.
Принсгейм А.
Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес.
Часто построение графиков связано с исследованием поведения функций. Однако необходимость построения графиков не ограничивается только этим. В ряде случаев графики облегчают нахождение решений уравнений и неравенств, сокращая и упрощая аналитические выкладки, и часто при этом являются единственным методом решения таких задач.
Не все учащиеся владеющие теорией успешно справляются с построением графиков, причины бывают разные: недостаток терпения, аккуратности или интереса. Но рисовать любят многие, поэтому если объединить рисование и построение графиков, то можно добиться отличного результата.
На своих уроках при изучении темы «График квадратичной функции» я применяю подобное объединение следующим образом. На начальном этапе даю готовые уравнения на заданном отрезке и предлагаю изобразить графики в системе координат. Более продвинутым учащимся я предлагаю самим нарисовать рисунок и попробовать задать его с помощью графиков по следующей схеме
1 этап
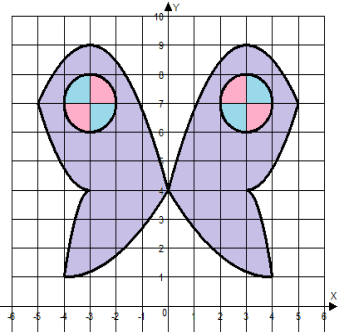
Рисуем, например, крылья бабочки
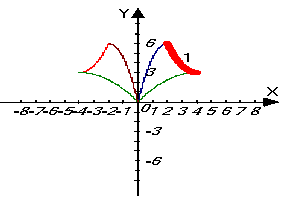
Рис. 1.
2 этап
Определим линию, которую хотим задать с помощью уравнения № 1. Пусть точка (4;3) — вершина параболы (1), построим систему новую систему координат в вершине.
![]()
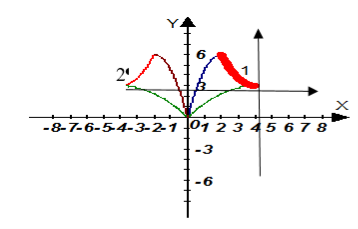
Рис. 2.
Таким образом, уравнение вида ![]() новой системе координат примет более простой вид
новой системе координат примет более простой вид ![]() задача сводиться к нахождению коэффициента a.
задача сводиться к нахождению коэффициента a.
3 этап
Вычислим a, подставляя в уравнение координаты второй точки (в новой системе):(-2;3)
![]()
![]()
![]()
4этап
Вернемся к основной системе координат и получим уравнение
![]() Значит, линия 1 на рисунке задана формулой
Значит, линия 1 на рисунке задана формулой
![]() . Но нам требуется не вся парабола, а лишь та её часть, которая лежит на промежутке
. Но нам требуется не вся парабола, а лишь та её часть, которая лежит на промежутке ![]() .
.
Получим линию 1 на рисунке 1.
Продолжая дальше, получаем: уравнение для линии 2
![]() .
.
Очевидно, что составлять уравнения для графиков симметричных относительно оси ОУ проще, т. к. меняются только координаты вершины параболы в «новой системе координат»
В таблице представлены несколько рисунков и соответствующих им уравнений
|
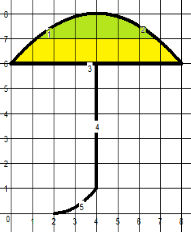
Зонтик |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
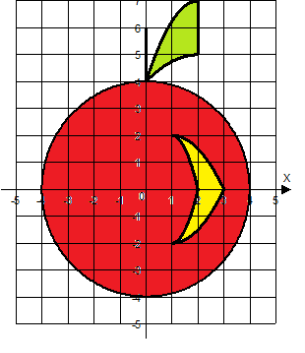
Яблоко |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Бабочка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
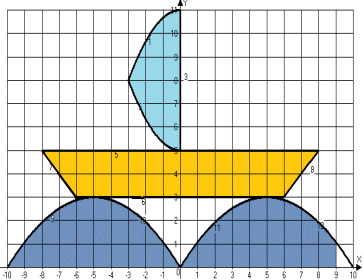
Лодка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|