В этой работе описывается методика решения задач и численных результатов о распространении волн в бесконечных протяженных пластинках переменной толщины. Вязкие свойства материала учитываются с помощью интегрального оператора Вольтера. Исследование проводится в рамках пространственной теории вязкой упругости. Методика основана на разделении пространственных переменных и формулировании краевой задачи на собственные значения, которые решаются методом ортогональной прогонки Годунова. Получены числовые значения реальной и мнимой части фазовой скорости в зависимости от волновых чисел. При этом получено совпадение числовых результатов с известными данными.
Ключевые слова: пластинка, переменная толщина, вязкие свойства, ортогональная прогонка, фазовая скорость, волна.
Известно [7, 8], что нормальные волны в деформируемом слое (волны Лэмба) не ортогональны по толщине слоя, т. е. интеграл от скалярного произведения векторов смещений двух различных волн, рассматриваемых как функции координаты, перпендикулярной поверхностям слоя, не равен нулю. Они также не ортогональны сопряженным волнам, получающимся из рассмотрения сопряженной задачи. Это обстоятельство вносит дополнительные трудности при решении практических задач [2, 4, 9]. В этой работе построена сопряженная спектральная задача и условия биортогональности для рассматриваемой задачи.
Математическая постановка задачи
Рассматриваем вязкоупругий волновод в виде бесконечной вдоль оси Х1 переменной толщины (рис. 1). Основные соотношения классической теории пластин переменной толщины можно получить на основе принципа возможных перемещений. Вариационное уравнение задачи теории вязкоупругости в трехмерной постановке имеет вид
![]()
![]() ,(1)
,(1)
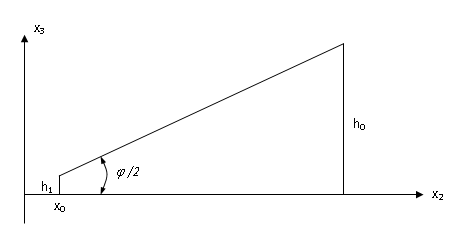
Рис. 1. Расчетная схема пластин переменной толщины
где ρ – плотность материала; ![]() i — компоненты перемещений; ij и ij — компоненты тензора напряжений и деформаций; V — объем, занимаемый телом. В соответствии с гипотезами Кирхгофа-Лява
i — компоненты перемещений; ij и ij — компоненты тензора напряжений и деформаций; V — объем, занимаемый телом. В соответствии с гипотезами Кирхгофа-Лява
Пренебрегая в (1) членами, учитывающими инерцию вращения нормали к срединной плоскости, будем иметь следующее вариационное равенство:
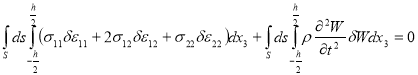 (3)
(3)
Исходя из геометрических соотношений и соотношений обобщенного закона Гука с учетом кинематических гипотез (2) выражения для компонент тензоров деформаций и напряжений имеют вид
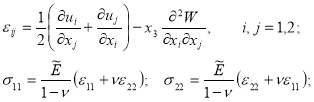 (4)
(4)
![]()
где ![]() – операторный модуль упругости, который имеет вид [5]:
– операторный модуль упругости, который имеет вид [5]:
![]() (5)
(5)
![]() — произвольная функция времени;
— произвольная функция времени; ![]() — ядро релаксации;
— ядро релаксации; ![]() — мгновенный модуль упругости;
— мгновенный модуль упругости; ![]() — коэффициент Пуассона, предлагается, что постоянная величина; принимаем интегральные члены в (5) малыми, тогда функции
— коэффициент Пуассона, предлагается, что постоянная величина; принимаем интегральные члены в (5) малыми, тогда функции ![]() , где
, где ![]() – медленно меняющаяся функция времени,
– медленно меняющаяся функция времени, ![]() – действительная константа. Далее, применяя процедуру замораживания [1], заменим соотношения (2) приближенными вида:
– действительная константа. Далее, применяя процедуру замораживания [1], заменим соотношения (2) приближенными вида:
![]() .
.
Здесь ![]() ,
, 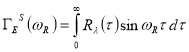 – соответственно косинус и синус ‑ образы Фурье ядра релаксации материала.
– соответственно косинус и синус ‑ образы Фурье ядра релаксации материала.
Вводя обозначение для моментов
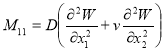 ;
;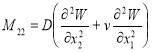 ;
; ![]()
и интегрируя по толщине полосы, приведем равенства (3) ее к следующему виду
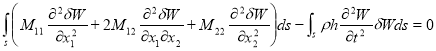 (6)
(6)
Интегрируя дважды по частям и приравнивая к нулю коэффициенты при вариациях ![]() W внутри тела и на его границе, получаем следующее дифференциальное уравнение
W внутри тела и на его границе, получаем следующее дифференциальное уравнение
![]() (7)
(7)
с естественными граничными условиями
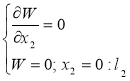 (8)
(8)
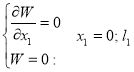 (9)
(9)
и главными альтернативными к ним
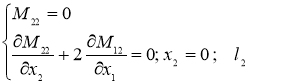 (10)
(10)
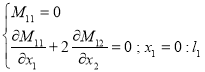 (11)
(11)
Для построения спектральной задачи введем следующую замену переменных:
W=W; ![]()
![]()
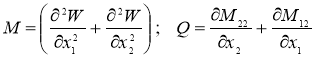 (12)
(12)
Подставляя (12) в (7), получим систему дифференциальных уравнения в частных производных, разрешенную относительно первых производных по х2:
![]() ;
;
![]() ;
;
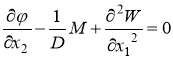 (13)
(13)
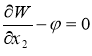 :
:
и альтернативные граничные условия на х2 = 0: x2 = l2:
![]() или
или 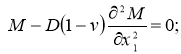 (14)
(14)
![]() или
или ![]() и на х1=0, х1=l1,
и на х1=0, х1=l1,
Рассмотрим теперь бесконечную вдоль оси х1 полосу с произвольным законом изменения толщины* h=h(x2). Будем искать решение задачи (13) - (15) в виде
![]() ,(16)
,(16)
описывающие гармонические плоские волны, распространяющиеся вдоль оси х1. Подставляя (16) в (13), получим дифференциальные уравнения первого порядка, разрешенные относительно производных
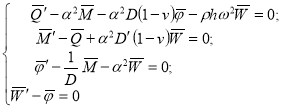 (17)
(17)
с граничными условиями на торцах полосы х2=0, l2, одного из четырех типов:
шарнирное опирание: ![]() (18)
(18)
скользящий зажим: ![]() (19)
(19)
жесткая заделка: ![]() (20)
(20)
свободный край: 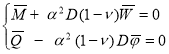 (21)
(21)
Таким образом, сформулирована спектральная задача (17 - 21) по параметру 2, описывающая распространение изгибных плоских волн в волноводе, выполненном в виде полосы с произвольным законом изменения толщины по координате х2. Показано, что спектральный параметр 2 принимает только действительные значения (при RE =0).
Преобразуя для этого систему (17), имеем:
![]() , откуда
, откуда
![]() .
.
Кроме того:
![]() .
.
Таким образом, преобразованная система имеет вид:
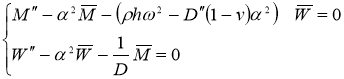 (22)
(22)
Граничные условия (18–21) в переменных ![]() имеют вид:
имеют вид:
шарнирное опирание: ![]() (23)
(23)
скользящий зажим: ![]() (24)
(24)
жесткая заделка: ![]() (25)
(25)
свободный край:
при х2=0 или х2=+е2
Пусть ![]() и
и ![]() некоторые собственные функции системы (22)‑(26), возможно комплексное значение. Помножим уравнения системы (22) на
некоторые собственные функции системы (22)‑(26), возможно комплексное значение. Помножим уравнения системы (22) на ![]() и
и ![]() , комплексно сопряженные к функциям
, комплексно сопряженные к функциям ![]() и
и ![]() . Тождественно преобразовав первое уравнение, проинтегрируем полученные равенства по х2 и составим следующую линейную комбинацию:
. Тождественно преобразовав первое уравнение, проинтегрируем полученные равенства по х2 и составим следующую линейную комбинацию:
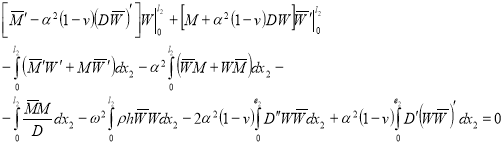 (27)
(27)
Легко убедиться, что члены, не входящие в интегралы равенства (27), обращаются в нуль при любой комбинации граничных условий (23)‑(26). Необходимо заметить также, что все подинтегральные функции действительны. Выражая 2 из (27), получим (RE =0), что
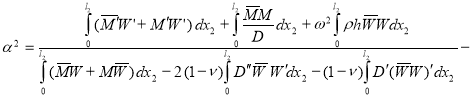 действительное число. Таким образом показано, что квадрат собственного волнового числа для бесконечной полосы переменной толщины действителен при любой комбинации граничных условий.
действительное число. Таким образом показано, что квадрат собственного волнового числа для бесконечной полосы переменной толщины действителен при любой комбинации граничных условий.
Заключение
- На основе вариационного уравнения теории упругости предложена математическая постановка задачи о распространении волн в протяженных пластинках переменной толщины. Получены системы дифференциальных уравнений с соответствующим граничным условием.
- Установлено, что квадрат собственного волнового числа для бесконечной полосы переменной толщины действителен при любой комбинации граничных условий.
- Сформулированная спектральная задача не является самосопряженной. Построена для нее сопряженная задача. Сопряженная система состоит из обыкновенных дифференциальных уравнений с соответствующим граничным условием. С помощью формулы Лагранжа получены условия биортогональности форм. Поставленная задача решается численно, методом ортогональной прогонки С. К. Годунова в сочетании с методом Мюллера.
Литература
- Бозоров, М. Б.; Сафаров, И. И.; Шокин, Ю. И. Численное моделирование колебаний диссипативно однородных и неоднородных механических систем. СО РАН, Новосибирск, 1996. – 188 с.
- Гахов, Ф. Д. Краевые задачи. М.: Физматгиз, 1963. – 639 с.
- Годунов, С. К. О численных решениях краевых задач для систем линейных обыкновенных дифференциальных уравнений. — Успехи математических наук, 1061, Т. 16, вып. 3, ‑ С 171–174.
- Гринченко, В. Т.; Мелешко В. В. Гармонические колебания и волны в упругих телах. К.: Наука думка, 1981. – 283 с.
- Колтунов, М. А. Ползучесть и релаксация. М.: Высшая школа, 1976. –
276 с.
- Неймарк, М. А. Линейные дифференциальные операторы. М.: Наука, 1969. – 526 с.
- Сафаров, И. И.; Болтаев, З. И. Распространение гармонических волн в пластинке переменной толщины. Изв. высших учебных заведений. Поволжский регион. Серия: физ.–мат. науки, № 4, 2011. ‑ С. 31–39.
- Сафаров, И. И.; Тешаев, М. Х.; Болтаев, З. И. Волновые процессы в механическом волноводе. LAP LAMBERT Academic publishing (Германия). 2012. ‑ 217 с.
- Сунчалиев, Р. М.; Филатов, А. О некоторых методах исследования нелинейных задач теории вязкоупругости //ДАН СССР, 1972. ‑ № 1. с. 201–203.







