В этой работе изучается поле динамических напряжений и смещений, возникающее вблизи цилиндрической полости (подкрепленной или неподкрепленной) в вязкоупругой среде при прохождении плоской волны. Показано, что в случае неподкрепленной полости динамические напряжения зависят от волнового числа падающей волны, от коэффициента Пуассона и от параметров ядра релаксации, а также от мгновенного модуля упругости.
Ключевые слова: потенциалы перемещений, напряженно-деформированное состояние, продольные и поперечные волны, гармонических волны, метод Гаусса
Введение. Воздействие продольных и поперечных волн на цилиндрическое тело, исследовалось многими авторами [1, 2, 3, 4]. При этом рассматривались осе симметричные, (не осе симметричные) задачи применялись различные модели для жидкости и слоя (или оболочек). В предыдущих работах цилиндрическое тело рассматривалось в виде цилиндрической оболочки и уравнение движения получено на основе гипотезы Кирхгофа — Лява [5,6,7,8]. Также окружающая среда рассматривалась как упругая, т. е. связь напряженного и деформированного состояния подчиняется закону Гука [9,10]. Настоящая работа отличается от предыдущих тем, что цилиндрическую оболочку окружает среда, обладающая вязкие свойства, т. е. связи напряжения и деформации подчиняются интегральному соотношению Больцмана — Вольтера [12]. Модели воздействия продольных и поперечных волн на цилиндрические слои и жидкости базируются на методах, которые разработаны в динамике тел, взаимодействующих с деформируемой средой, например, в книге [11].
Подстановка задачи. На бесконечно длинный, однородный, изотропно-деформируемый цилиндр, находящийся в бесконечной вязкоупругой среде, падает гармоническая плоская волна расширения (или сдвига) (рис.1). Фронт волны является параллельным оси цилиндра. Таким образом, рассматривается задача о плоской деформации. Здесь ![]() внешнего и
внешнего и ![]() -внутреннего радиусов цилиндрического слоя. Основной целью работы является определение напряженно — деформированного состояния цилиндрического слоя и окружающей среды при воздействии продольных (или поперечных) гармонических волн. В предположении обобщенного плоско деформированного состояния уравнение движения в смещениях имеет вид [1]
-внутреннего радиусов цилиндрического слоя. Основной целью работы является определение напряженно — деформированного состояния цилиндрического слоя и окружающей среды при воздействии продольных (или поперечных) гармонических волн. В предположении обобщенного плоско деформированного состояния уравнение движения в смещениях имеет вид [1]
![]() (1)
(1)
где ![]() и
и![]() (
(![]() ,
, ![]() -относятся к окружающей среде,
-относятся к окружающей среде, ![]() - к слою) операторные модули упругости
- к слою) операторные модули упругости
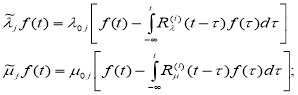 (2)
(2)
![]() — вектор плотности объемных сил
— вектор плотности объемных сил ![]() ;
; ![]() — некоторая функция;
— некоторая функция; ![]() — плотности материалов,
— плотности материалов, ![]() и
и ![]() -ядро релаксации,
-ядро релаксации, ![]() -мгновенные модули упругости вязкоупругого материала,
-мгновенные модули упругости вязкоупругого материала, ![]() -вектор смещения, который зависит от
-вектор смещения, который зависит от ![]() . На контакте двух тел r= R выполняется равенство смещений и напряжений (условие жесткого контакта)
. На контакте двух тел r= R выполняется равенство смещений и напряжений (условие жесткого контакта)
![]()
![]()
![]()
![]() . (3)
. (3)
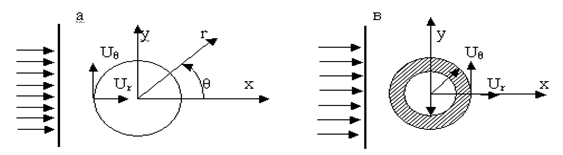
Рис. 1. Цилиндрическое тело, находящееся в деформируемой среде: а. цилиндрическая полость; в. цилиндрическая оболочка
Отметим, что в случае скользящего контакта грунта по поверхности трубы последнее уравнение в (3) примет вид [2,10,11,13]: ![]() .
.
Пусть падающая плоская волна распространяются в положительном направление оси х: ![]() -при воздействии продольных волн (или
-при воздействии продольных волн (или ![]()
![]() - при воздействии волн сдвига);
- при воздействии волн сдвига); ![]() и
и ![]() -величины амплитуды падающих волн;
-величины амплитуды падающих волн; ![]() -круговая частота падающих волн; α1 и β1 — волновое число, которое может быть комплексным числом α1 = αR1 + i αI1;
-круговая частота падающих волн; α1 и β1 — волновое число, которое может быть комплексным числом α1 = αR1 + i αI1;
β1 = βR1+ i βI1, αI1< 0 и βI1< 0 обозначают коэффициенты затухания; αR1 и βR1 обозначает волновое число продольных волн и волн сдвига соответственно. Выражение ![]() (или
(или ![]() ) можно представить в полярных координатах цилиндрического слоя
) можно представить в полярных координатах цилиндрического слоя ![]() посредства ряда
посредства ряда
![]() (4)
(4)
где ![]() ,
, ![]() -цилиндрическая функция Бесселя первого рода.
-цилиндрическая функция Бесселя первого рода.
Методы решения
Поставленная задача решается в потенциалах перемещений, для этого представим вектор перемещения в виде:
![]() ,
,
где ![]() — потенциал продольных волн;
— потенциал продольных волн; ![]() — векторного потенциала поперечных волн.Основные уравнения теории вязко упругости (1) для этой задачи о плоской деформации сводятся к следующему уравнению
— векторного потенциала поперечных волн.Основные уравнения теории вязко упругости (1) для этой задачи о плоской деформации сводятся к следующему уравнению
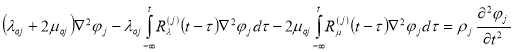
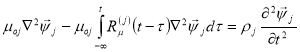 (5)
(5)
где ![]() – дифференциальные операторы в цилиндрических координатах и
– дифференциальные операторы в цилиндрических координатах и ![]() — коэффициент Пуассона [12].
— коэффициент Пуассона [12].
На бесконечности r → ∞потенциалы продольных и поперечных волн при![]() удовлетворят условию излучения Зоммерфельда [1]:
удовлетворят условию излучения Зоммерфельда [1]:
![]()
![]() , (6)
, (6)
![]()
![]() .
.
Решение уравнения (5) можно искать в виде:
![]() (7)
(7)
где ![]() и
и ![]() — комплексная функция, которое является решение уравнениям
— комплексная функция, которое является решение уравнениям
![]()
![]() (8)
(8)
где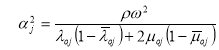 ,
, 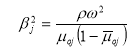 ,
,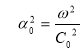
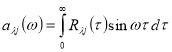 ,
, 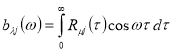 .
.
Решение уравнения (5) с учетом (8) выражается через функции Ханкеля 1-го и 2-го рода n-го порядка:
![]()
![]()
![]() (9)
(9)
![]()
где ![]() и
и![]() – коэффициенты разложения, которые определяются соответствующими граничными условиями;
– коэффициенты разложения, которые определяются соответствующими граничными условиями; ![]() и
и ![]() — соответственно функция Ханкеля 1-го и 2-го рода n-го порядка
— соответственно функция Ханкеля 1-го и 2-го рода n-го порядка![]() . Решение (9) при j=1 удовлетворяет на бесконечности r→∞условию излучения Зоммерфельда (6) и представляется в виде:
. Решение (9) при j=1 удовлетворяет на бесконечности r→∞условию излучения Зоммерфельда (6) и представляется в виде:
![]()
Полный потенциал можно определить путем наложения потенциалов падающих и отраженных волн. Таким образом, потенциалы смещений будут
![]() ,
,![]() (10)
(10)
Отсюда следует, что напряжения, и смещения легко могут быть выражены через потенциалы смещений [2],
![]() (11)
(11)
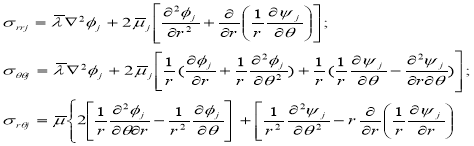
После подставляя (10) в (11) с учетом (9), получим следующее выражение для перемещения и напряжения:
![]()
![]()
![]()
![]()
![]()
![]() (12)
(12)
![]()
![]()
![]() где
где
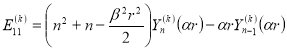
![]()
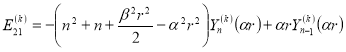
![]()
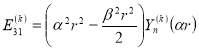
![]()
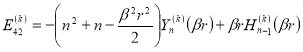
![]()
![]()
![]()
где ![]() .
.
Неопределенные коэффициенты ![]() определяются из системы линейных алгебраических уравнений седьмого порядка
определяются из системы линейных алгебраических уравнений седьмого порядка
![]() (13)
(13)
где {q}-вектор столбец, содержащий произвольные постоянные; {F}-вектор столбец внешних нагрузок; [C]-квадратная матрица, элементы -которого выражаются через функции Бесселя и Ханкеля. Уравнение (13) решается методом Гаусса с выделением главного элемента [14]
Результаты расчетов ивыводы
Для данных падающих волы напряжения и смещения определяются рядами, описываемыми выражениями (9)-(12) в случае жесткого контакта. Вычисления были выполнены на компьютерном программном комплексе «Matlab», ряды вычислены с точностью до 10–8. С увеличением их аргумента ряд (9)–(11) сходится. Поэтому на основе численных экспериментов установлено, что точность из 5–6 членов ряды точность достигла 10–6–10–8. В качестве ядра релаксации вязкоупругого материала примем трехпараметрическое ядро ![]() Рижаницена –Колтунова [3], обладающее слабое сингулярностью, где
Рижаницена –Колтунова [3], обладающее слабое сингулярностью, где ![]() -параметры материалы [3]. Примем следующие параметры:
-параметры материалы [3]. Примем следующие параметры:![]() ;
;![]()
В табл. 1 приведены значения контурного напряжения в зависимости от α0а, полученные в работе [2] и наши результаты.
Таблица 1
Контурное напряжение | σ*θθ| (σθθ / σ0) взависимости от волнового числа (θ = π / 2).
|
α0а |
PaoY.H., MowC.C. |
Наши результаты |
|
|
[2] |
R (t) =0 |
При малой вязкости |
|
|
0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 |
2.254366 1.862148 1.715704 1.701800 1.471240 1.266527 1.370846 1263184 |
2.225087 1.863807 1.718236 1.703247 1.473521 1.268716 1.372605 1.265393 |
1.983207 1.710337 1.589253 1.513627 1.309041 1.127835 1.197730 1.065339 |
При воздействии поперечных волн в цилиндрической полости максимальное контурное напряжение достигнет значения ![]() .
.
Учет вязких свойств материала (или окружающей среды) при расчете на действие продольных и поперечных гармонических волн, снижает напряжения и перемещения на 10–16 %. Максимальное радиальное напряжение при воздействии продольных волн достигается в = 900 и 2700.Следует отметить, что максимальное радиальное напряжение при воздействии поперечных волн достигается в = 450 и 1350; а также распределение напряжение при 1R1= 0,099 почти такой же как в статическом случае (λ→ ∞), в то время как при более высоких волновых (![]() ) числах распределение напряжений значительно отличается от статического. Отношения плотностей =1/2 оказывает большое влияние на напряжения и смещения слоя. По мере возрастания плотности слоя максимальные величины напряжения и смещения слоя возрастают. Таким образом, разработанная методика и алгоритм для решения поставленных задач, позволяют найти напряженно-деформированное состояние цилиндрических тел при воздействии гармонических волн.
) числах распределение напряжений значительно отличается от статического. Отношения плотностей =1/2 оказывает большое влияние на напряжения и смещения слоя. По мере возрастания плотности слоя максимальные величины напряжения и смещения слоя возрастают. Таким образом, разработанная методика и алгоритм для решения поставленных задач, позволяют найти напряженно-деформированное состояние цилиндрических тел при воздействии гармонических волн.
Литература:
- Гузь А. Н., Кубенко В. Д., Черевенко М. А. Дифракция упругих волн. «Наук», 1978. 308 с.
- Pao Y. H., Mow C. C. diffraction of elastic waves and dynamic stress concentration. № 4, Grane, Russak, 1973 694 p.
- Колтунов М. А. Ползучесть и релаксация. — М.: Высшая школа, 1976.- 276с.
- Datta S. K. Tensional waves in an infinite elastic solid containing a penny — shaped crack.-z. answer. Math. And Phys., 1970, 21, № 3, р.343–351
- Мубариков Я. Н., Сафаров И. И. О действии упругой волны на цилиндрическую оболочку. Изв.АнУзССР, серия технических наук, 1987. № 4. с. 34–40
- Сафаров И. И. Оценка сейсмонапряженного состояния подземных сооружений методики волновой динамики Сборник «Сейсмодинамика заданий и сооружений» Ташкент, Фан. 1988.
- Филиппов И. Г., Егорычев О. А. Нестационарные колебания и дифракция волн в акустических и упругих средах.. — М.: Машиностроение, 1977.-304 с.
- Сафаров И. И. Взаимодействие волн в многослойных цилиндрических слоях, находящихся в безграничной упругой среде. Труды VII вссоюз. конференция «Динамика основный, фундаментов и подземных сооружений» Днепропетровск, 1989. с. 56–57
- Сафаров И. И., Жумаев З. Ф. О разрушении тоннеля при сильных движениях земли. Международная конференция по сейсмостойкому строительству. С-Петрбург, 2000, с. 71–78
- Авлиякулов Н. Н., Сафаров И. И. Современные задачи статики и динамики подземных трубопроводов. Ташкент, Fanvatexnologiya. 2007. 306 с.
- Бозоров М. Б., Сафаров И. И., Шокин Ю. И. Численное моделирование колебаний диссипативно однородных и неоднородных механических систем. Новосибирск: Изд. СО РАН. 1996.189 с.
- Рашидов Т. Р., Сафаров И. И. и др. О двух основных методах изучения сейсмонапряженного состояния подземных сооружений при действии сейсмических волн. Ташкент: ДАН. № 6, 1989. С. 13–17.
- Сафаров И. И. Авлиякулов Н. Н. Методы повышения сейсмостойкости подземных пластмассовых трубопроводов // Узбекский журнал нефти и газа, 2005, № 4.С.42–44.
- Грейс Э., Мэтьюз Г. Б. Функции Бесселля и их приложение к физике и механике.-М.: Изд.воиностр.лит., 1953, — 371 с.







