Геометрическое образование должно начинаться с первых шагов пребывания ученика в школе — на уроках труда, природоведения, рисования, а в средних классах — географии и черчения.
Геометрия — это «не только раздел математики, школьный предмет, это, прежде всего, феномен общечеловеческой культуры, являющийся носителем собственного метода познания мира».
В настоящее время изучение систематического курса геометрии начинается с 7 класса средней школы. Однако со многими геометрическими фигурами посредством практической деятельности дети знакомятся намного раньше. Это происходит уже на занятиях в детском саду и на уроках рисования, труда, математики в начальной школе.
В большинстве школ элементы геометрии в 5–6 классах изучаются в рамках одного предмета: математики. В связи с этим возникает вопрос о совершенствовании методики изучения элементов геометрии в курсе математики 5–6 классов.
Цель нашей работы заключается в следующем- показать возможность непрерывного изучения геометрии на уроках математики, а также на кружках, составить задачный материал для данной работы.
При описании психических процессов детей 11–13 лет будем опираться на психические особенности младших школьников, поскольку дети 5–6 классов близки к младшему школьному возрасту.
Как показали исследования психологов, возраст детей от 7–12 лет наиболее благоприятен для формирования геометрических представлений. Детям этого возраста присуще яркость восприятия, наглядная образная память, большой интерес к окружающему миру, богатое воображение, способность легко усваивать материал и др.
Ещё в дошкольном возрасте ребёнок встречается с различными линиями, фигурами, поверхностями, формами, под влиянием которых у него формируются геометрические представления. Геометрические представления в этом возрасте носят случайный и хаотичный характер, они не всегда правильные, преимущественно «плоскостные». В начальной школе продолжается процесс накопления детьми представлений о пространстве, необходимых для усвоения элементарных понятий, а затем учащиеся приступают к дальнейшей стадии обобщения и конкретизации свойств и отношений предметов и явлений материального мира по разным признакам: временным, количественным, пространственным.
На уроках математики в начальной школе имеют большое значение практические работы: изготовление геометрических фигур, их вычерчивание, вырезание, получение прямого угла перегибанием бумаги, упражнения на формирование навыков работы с наиболее употребляемыми чертёжными инструментами (линейка, угольник, циркуль). Большое внимание уделяется приёму сопоставления и противопоставления фигур.
В начальной школе учащиеся должны уметь:
1 класс:
‒ изображать прямую, кривую, отрезок, многоугольник;
‒ находить длину отрезка в см;
‒ начертить отрезок заданной длины;
‒ увеличить или уменьшить отрезок на заданное количество см;
‒ различать углы прямые и непрямые, прямоугольники и квадраты;
‒ распознавать эти фигуры, называть их и изображать на клеточной бумаге;
2 класс:
‒ делить отрезок на равные части;
‒ распознавать и изображать ломаную, окружность, круг, многоугольник;
‒ измерять длину ломаной.
К окончанию начальной школы пространственные представления учащихся становятся более осознанными, полными. Учащиеся, как правило, уже почти свободно ориентируются в пространстве, отмечают направления, определяют положение предметов по отношению к другим предметам, к сторонам горизонта. У них накоплен определённый запас геометрических представлений, терминов. Они могут узнавать пространственный объект в окружающей действительности и находить его графическое изображение. Учащиеся уже могут воспроизвести несложные представления в памяти, в воображении и словесно их описать, а также воспроизвести представления графически в виде предметной модели.
Уроки труда, рисования, математики содержат определённую систему предметов, методов и средств, создающих в уме школьника многообразную категорию пространственных представлений и отношений. Всё это определяет содержание пропедевтической работы учителя по развитию геометрических представлений учащихся начальных классов.
Наши первые учителя — наши руки, ноги, глаза. Заменить все это книгами, это значит научить нас не рассуждать, а пользоваться разумом других людей; это значит научить нас многое принимать на веру и никогда ничего не знать. Руссо
1.1 Упражнения, направленные на развитие графической культуры
Характеристика заданий:
‒ задания на развитие тонкой моторики руки;
‒ задания на наблюдательность, внимательность и аккуратность;
‒ навыки работы с циркулем и линейкой.
Учимся чертить правильно.
- Начертите по линейке и линии тетради несколько линий так, чтобы они не пересекались.
- Возьмите угольник и обрисуйте его. Рядом повторите то же самое, не обрисовывая, а используя только одну сторону линейки.
- Возьмите циркуль и начертите окружность
а) любого радиуса.
б) радиуса 2 см.
- Дорисуйте окружность
- Начертите кусок орнамента в тетради и продлите его по всей длине страницы.
- Положите 12 спичек так, чтобы получилось 5 квадратов. Переложите 3 спички так, чтобы получилось 3 равных квадрата.
В геометрии очень важно уметь смотреть и видеть, замечать различные особенности геометрических фигур, делать выводы из замеченных особенностей. Эти умения, которые вместе можно назвать «геометрическим зрением», необходимо постоянно тренировать и развивать.
Задачи по геометрии, решаемые методами оригами
Слово «оригами» происходит от двух японских слов: «ори» — сложенный, «ками» — бумага, и может быть переведено как «сложенная бумага». Складывание фигурок из бумаги имеет многовековую историю и своими корнями тесно связано с культурой Востока.
Неопределяемыми понятиями геометрии являются: точка, прямая и плоскость. В традиционном школьном курсе геометрии решаются задачи на построение при помощи циркуля и линейки. В решении таких задач с помощью линейки можно провести произвольную прямую; произвольную прямую, проходящую через данную точку; прямую, проходящую через две данные точки. При помощи циркуля можно описать окружность данного радиуса и отложить отрезок на данной прямой от данной точки.
Возможности перегибания листа бумаги включают в себя не только «геометрию линейки», но и «геометрию циркуля», что обеспечивает возможность решения большого разнообразия серьезных, а порой и забавных задач. Как правило, решение задач методами перегибаний (оригами) проще и нагляднее. Некоторые задачи, решаемые методами оригами, при помощи циркуля и линейки просто не имеют решения!
Наглядность и относительная простота освоения оригами могут помочь и при изучении геометрии. Такой подход оживляет и заметно облегчает освоение целого ряда абстрактных, и потому сложных для освоения многим учащимся геометрических понятий, делает их изучение более ясным и доступным, убеждает в правильности классических утверждений, теорем и побуждает к дальнейшим исследованиям. Ученики учатся понимать то, о чем говорят сами, и то, что говорят другие, учатся мыслить.
Из произвольного листа бумаги при помощи сгибов можно получить квадрат. Если на этом листе бумаги дан отрезок, который требуется разделить, то всегда сначала можно построить квадрат со стороной равной этому отрезку, а затем разделить сторону квадрата.
В задачах этого раздела происходит деление на равные части стороны квадрата (прямоугольника) при этом подразумевается, что длина заданного отрезка равна стороне квадрата.
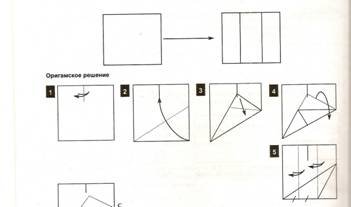
Методом перегибания точно разделить сторону квадрата на три равные части.
Геометрия на клетчатой бумаге
Рекомендации по проведению уроков
‒ Начинать обучать школьников желательно с пятого класса.
‒ Преподавание должно вестись непринужденно, почти в импровизационном стиле. Эта видимая легкость на самом деле требует от учителя большой и серьезной подготовки.
‒ Занятия лучше проводить в нестандартной форме.
‒ Необходимо использовать на уроках как можно больше наглядного материала: различных карточек, картинок, наборов фигур, иллюстраций к решению задач, схем.
‒ При разборе темы нужно стараться добиваться понимания, а не зазубривания.
Исследуя структуру пропедевтического курса геометрии, мы пришли к выводу, что формирование начальных геометрических представлений может проходить в рамках одного предмета — математики, однако с целью углубления и расширения интеллектуального уровня учащихся и развития их пространственных представлений можно изучать элементы геометрии отдельным блоком.
Литература:
- Белим, С. Н. Задачи по геометрии, решаемые методами складывания (оригами) [Текст] — М.: Аким, 1998]
- Гусев, В. А. Психолого-педагогические основы обучения математике // В. А. Гусев. — М.: Вербум, Академия, 2003. — 432 с.
- Методика обучения геометрии [Текст]: Учеб. Пособие для студ. Высш. Пед. Учеб. Заведений / В. А. Гусев, В. В. Орлов, В. А. Панчищина и др.; Под ред. В. А. Гусева.-М.: Академия.-2004.-368 с.







