В статье анализируются задача на устойчивость железобетонного изгибаемого элемента под действием равномерно распределенного изгибающего момента, решенная ПК «ANSYS».
Определяются формы потери устойчивости и значение критического изгибающего момента. Итоговые значения сравниваются со значениями теоретических результатов по книге А. В. Перельмутера, В. И. Сливкера «Устойчивость равновесия конструкций и родственные проблемы» на стр. 582.
Ключевые слова: устойчивость, железобетонная балка, изгибаемый элемент, изгибающий момент, критические нагрузки
Железобетонная балка задана в виде двух КЭ-моделей:
1.В стрежневой, где изгибающий момент задан сосредоточенными моментами, приложенными на узлы.
2.В объемной, где рассматривалось два варианта закрепления балки: по нижней грани и на уровне половины высоты торца балки, а изгибающий момент задавался как пара сил, равномерно распределенных по верхней и нижней граням.
Момент задавался со значением mизг= 1 т∙м/м.
Определения критических моментов и форм потери устойчивости решались методом Ланцоша. Задавались 10 шагов нахождения критических моментов и соответствующих им потери устойчивости.
Таблица 1
Сопоставление результатов расчёта
|
|
|
Критический погонный изгибающий момент, mизг, |
||||
|
№задачи |
№формы |
|
ANSYS |
т∙м/м |
Теория |
δ(%) |
|
|
|
Стержневая |
Объмная |
Объмная |
[1] |
|
|
КЭ-модель |
КЭ-модель |
КЭ-модель* |
||||
|
1 |
1 |
756,727 |
723,615 |
657,227 |
755,567 |
0,154 |
|
2 |
1322,000 |
1350,000 |
1344,000 |
- |
||
*- закрепление по нижней грани балки.
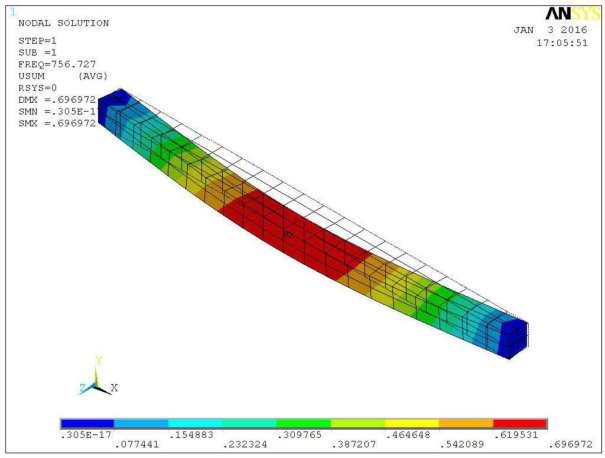
Рис. 1. 1-я форма потери устойчивости для объемной КЭ-модели (закреплена по нижней грани). mизг = 756,727 т·м/м
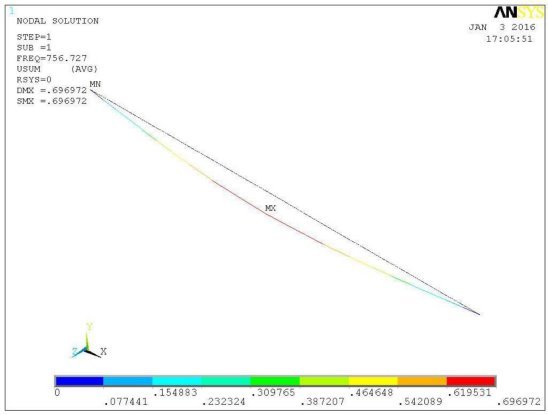
Рис. 2. 1-я форма потери устойчивости для стержневой КЭ-модели. mизг =756,727 т·м/м
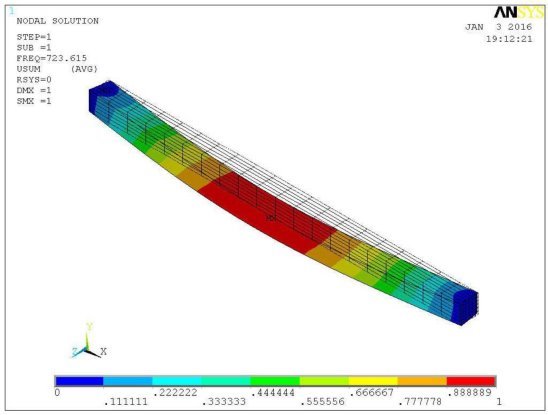
Рис. 3. 1-я форма потери устойчивости для объемной КЭ-модели (закреплена на уровне половины высоты торца). mизг = 723,615т·м/м

Рис. 4. 2-я форма потери устойчивости для объемной КЭ-модели (закреплена по нижней грани). mизг = 1322,000т·м/м
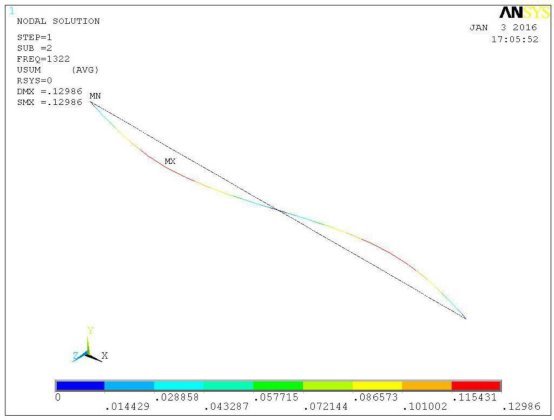
Рис. 5. 2-я форма потери устойчивости для стержневой КЭ-модели. mизг =1322,000т ·м/м

Рис. 6. 2-я форма потери устойчивости для объемной КЭ-модели (закреплена на уровне половины высоты торца). mизг = 1344,000·м/м
Литература:
- Перельмутер А. В., Сливкер В. И. Устойчивость равновесия конструкций и родственные проблемы — М.,“СКАД СОФТ”, 2007 — С. 551–554
- Баженов Ю. М. Технология бетона. — М.: Высшая школа, 1978.
- Ахметзянов Ф. Х. К особенностям деформирования, повреждаемости, изменения физико-механических характеристик бетона в конструкциях // Известия вузов. Строительство, 1993, № 9. — С. 150–155.
- Попов Л. Е., Пудан Л. Я., Колупаева С. Л., Кобытев В. С., Старенченко В. А. Математическое моделирование пластической деформации. — Томск, ТГУ, 1990. — С. 325.







