В данной статье исследуется зависимость максимального значения заболеваемости от выбора интенсивности и длительности вакцинации. Показывается, что при заданном объёме вакцинации эффективность её тем выше, чем быстрее она проводится.
Ключевые слова: вакцина, вакцинация, интенсивность, длительность
В современном мире один из основных способов борьбы с болезнями — это вакцинация. Чем больше людей ввели вакцину против болезни, тем меньшее количество людей может заразиться, и тем меньше шанс у этой болезни распространиться до уровня эпидемии. Для проведения ежегодной вакцинопрофилактики город ежегодно закупает большое число доз вакцин. Эффективность расхода этого количества зависит от выборов параметров вакцинации: её интенсивности и длительности. Выяснить эту зависимость можно моделируя развитие сезонного подъёма. Цель статьи — найти зависимость максимального значения заболеваемости от скорости и периода вакцинации.
Примем следующие обозначения:
Т — время вакцинации;
![]() — продолжительность эпидемии;
— продолжительность эпидемии;
t — данный момент времени;
U — интенсивность расходования вакцин.
![]() — текущий уровень заболеваемости
— текущий уровень заболеваемости
S — число восприимчивых к болезни;
I — число инфицированных;
R — число иммунных (переболевших);
![]() — число вакцинированных;
— число вакцинированных;
B — количество доз вакцин, закупленных городом;
a — коэффициент заражения![]()
b — коэффициент выздоровления;
β — коэффициент перехода из вакцинированных в иммунные.
На гиперболе![]() требуется построить зависимость максимального значения заболеваемости
требуется построить зависимость максимального значения заболеваемости ![]() от выбора параметров Т и U.
от выбора параметров Т и U.
![]() = max (
= max (![]() , (t ∈ [0,
, (t ∈ [0,![]() ]).
]).
Используя эти обозначения, составим систему уравнений:
![]()
![]()
![]()
Эту систему можно представить в виде схемы (Рис. 1):
Эту систему можно представить графически в следующем виде: 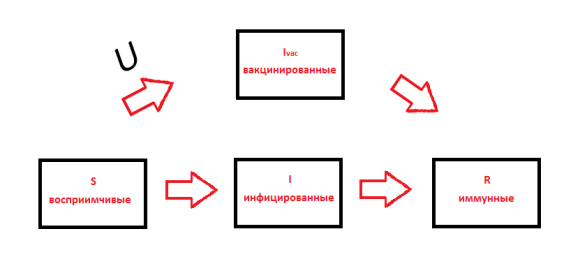
Рис. 1. Схема заболеваемости с учётом вакцинации
Используя данную систему, была построена модель в среде Simulink (Рис. 2):
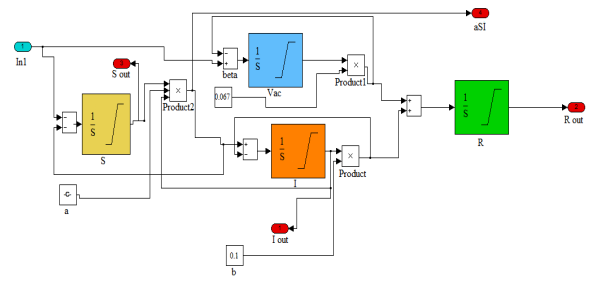
Рис. 2. схема заболеваемости, построенная с помощью среды Simulink
При помощи этой модели рассмотрим пример.
Пусть в городе проживает 1млн человек, 200тыс из которых инфицированные (I). Для вакцинации было закуплено 500 доз вакцин(B). Коэффициент заражения a = 0.0002, коэффициент заражения b = 0.1, коэффициент перехода из вакцинированных людей в иммунные β= 0.067. Рассматриваемый период времени — 200 дней (T). Тогда гипербола
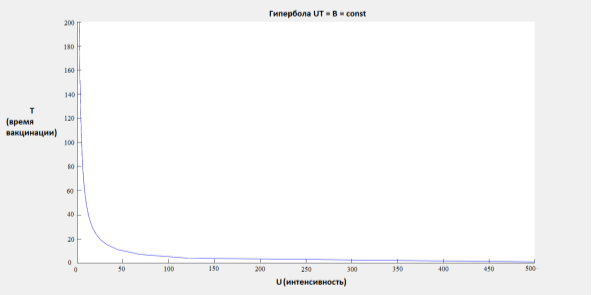
Рис. 3. вакцинация населения
На этой гиперболе выбираем ряд точек и вычисляем по ним максимальное значения заболеваемости ![]() . Составим таблицу зависимости максимального уровня заболеваемости (
. Составим таблицу зависимости максимального уровня заболеваемости (![]() от длительности (T) и интенсивности вакцинации (U) (Таблица 1). Из таблицы видно, что с увеличением скорости вакцинации (U) пик заболеваемости (
от длительности (T) и интенсивности вакцинации (U) (Таблица 1). Из таблицы видно, что с увеличением скорости вакцинации (U) пик заболеваемости (![]() понижается. При этом на графиках (Рис. 4) видно, что время продолжительности эпидемии увеличивается и максимальное количество инфицированных людей начинает резко снижаться.
понижается. При этом на графиках (Рис. 4) видно, что время продолжительности эпидемии увеличивается и максимальное количество инфицированных людей начинает резко снижаться.
Таблица 1
Зависимость максимального уровня заболеваемости от длительности иинтенсивности вакцинации
|
T (дни) |
U (человек вдень) |
|
|
40 |
12 |
0.18 |
|
35 |
14 |
0.13 |
|
30 |
16 |
0.125 |
|
25 |
20 |
0.08 |
|
20 |
25 |
0.065 |
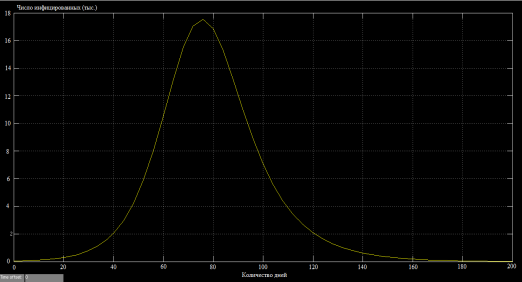
А) Заболеваемость людей без вакцинации
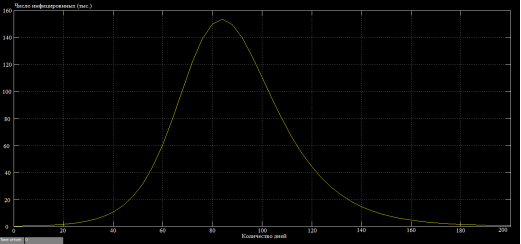
Б)Число инфицированных без вакинации
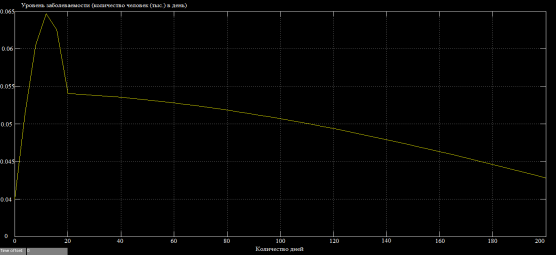
В) Заболеваемость людей с вакцинацией
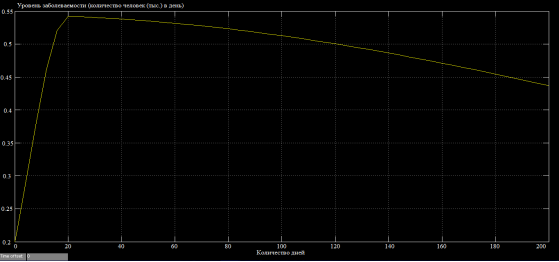
Г) Число инфицированных с вакцинацией
Рис. 4. Сравнение заболеваемости людей и числа инфицированных с вакцинацией и без неё
Вывод. В результате исследования мы выяснили: чем выше интенсивность вакцинации, тем ниже пик заболеваемости.
Литература:
- Колесин И. Д., Житкова Е. М. Математические модели эпидемий. — СПб.: СОЛО, 2017.
- Смирнов Н. В., Смирнов М. Н., Смирнова М. А. Решения прикладных задач теории управления в MATLAB. — СПб.: СОЛО, 2013. — 186 с.







