Аналитическая модель префиксного дерева на основе статистических свойств таблицы состояний и переходов



В работе предложена аналитическая модель структуры данных префиксного дерева, которая используется в работе алгоритма «лучевого» поиска информации. Рассматриваемая модель позволяет сократить время уплотнения разреженной таблицы состояний и переходов без нарушения целостности алгоритма поиска за счет учета статистических свойств структуры данных. Приведены теоретическое и экспериментальное обоснование адекватности предлагаемой модели.

Ключевые слова: алгоритм «лучевого» поиска, префиксные деревья, уплотнение структуры данных алгоритмов поиска текстовой информации

Развитие современных информационных технологий приводят к росту потребности в анализе больших объемов информации. Зачастую используются так называемые каталогизаторы и рубрикаторы, которые в свою очередь систематизируют и отбирают огромные объемы текстовой информации различного формата по ключевым словам. В качестве эффективного инструмента обнаружения в тексте ключевых слов используется алгоритм «лучевого» поиска [1], позволяющий обеспечить поиск и фильтрацию данных со скоростью, достигающей 500 Мбит/с. Однако при этом возникает проблема хранения большого объема данных в оперативной памяти вычислительных систем обработки. Специфика алгоритма «лучевого» поиска заключается в большой разреженности структуры данных префиксного дерева (СДПД), выступающего в качестве словаря признаков-ключей.

Проведенный анализ существующих алгоритмов уплотнения СДПД для ее эффективного хранения в оперативной памяти показал несостоятельность их применения в условиях использования словарей ключевых слов большого объема [2]. Ни один из известных алгоритмов уплотнения не удовлетворяет наиболее существенному требованию по приемлемой скорости обновления словаря. Таким образом возникает задача по разработке алгоритма уплотнения структуры словаря ключевых слов большого объема при ведении обработки текстовой информации, удовлетворяющего требованию по скорости и степени сжатия таблицы префиксного дерева.

Алгоритмизация процедуры уплотнения СДПД потребовала разработки принципиально новой модели, описывающей словарь ключевых слов для алгоритма «лучевого» поиска. В ходе научных исследований была выдвинута гипотеза о влиянии статистических характеристик СДПД на процесс ее уплотнения, что обусловило необходимость разработки теоретической доказательной базы для ее подтверждения. В результате было сформулировано и доказано утверждение о вероятности совместимости двух узлов префиксного дерева.

Утверждение. Вероятность совместимости двух случайно выбранных узлов и таблицы префиксного дерева равна:

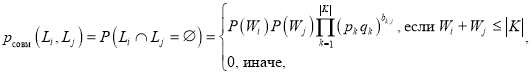(1)

где — вес узла префиксного дерева (сумма элементов столбца битовой карты), — мощность алфавита ключевых слов, — вероятности появления единичного и нулевого бита в k-й строке битовой карты префиксного дерева соответственно; – значение бита в карте для k-й строки i-го столбца. Под совместимостью понимается свойство двух столбцов и таблицы префиксного дерева, заключающееся в отсутствии одновременно ненулевых элементов двух столбцов одного индекса . Столбцы совместимы тогда и только тогда, когда каждая занятая ячейка одного столбца не соответствует любой занятой ячейке второго.

Доказательство. Совместимость двух случайно выбранных столбцов таблицы префиксного дерева есть пустое множество в пересечении и . Данное условие будет выполнено тогда, и только тогда, когда в битовом представлении столбцов в каждой позиции будет отсутствовать хотя бы одна «единица». С одной стороны рассмотрим вероятность появления единиц в столбце :

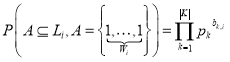. (2)

Так как для представления таблицы префиксного дерева вес столбца также представляет собой случайную величину, учтем вероятность выбора столбца с определенным весом. В этой связи выражение (2) примет вид

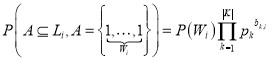. (3)

С другой стороны, пересечением двух столбцов будет пустое множество, когда в столбце будут отсутствовать единицы в позициях с единицами столбца . Принимая во внимание вероятность появления столбца c весом , вероятность такого события будет определена как

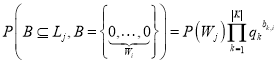. (4)

Случайный выбор столбцов для совмещения позволяет считать события независимыми и не учитывать условные вероятности их появления [3]. Тогда вероятность совместного события выбора столбцов и , пересечение которых есть пустое множество, с учетом необходимого условия совместимости двух столбцов , будет определена как

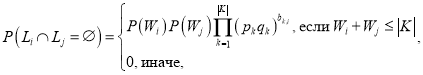
Что и требовалось доказать.

Следствие. Зависимость вероятности совместимости столбцов от вероятности появления единичного и нулевого бита в строке битовой карты, которая в свою очередь влияет на скорость процедуры уплотнения префиксного дерева, позволяет утверждать об адекватности разрабатываемой модели.

Назовем индексом номер строки матрицы состояний и переходов префиксного дерева, соответствующий ненулевому элементу. Очевидно, что есть дискретная случайная величина. В силу следствия можно утверждать о подтверждении гипотезы исследования, заключающейся в получении эффекта процедуры уплотнения префиксного дерева от учета статистических характеристик дискретной случайной величины . Возможность использования статистической модели структуры данных обусловлена неравномерностью распределения символов ее алфавита. В свою очередь подобная неравномерность вызвана проникновением статистики языка признакового пространства словарей ключей в статистику префиксного дерева. Например, «черные» списки URL составляются на основе символов английского языка, в этой связи распределение символов словаря ключевых английских слов будет схоже с распределением первообразного языка.

Использование в статистической модели моментов распределения случайной величины [4] повлекло за собой проведение экспериментальных исследований по:

‒ обоснованию достаточности мощности алфавита признаков «ключей» для вычисления статистических характеристик СДПД;

‒ выявлению зависимости эффективности процедуры уплотнения по показателям степени и скорости сжатия структуры префиксного дерева от количества используемых в модели моментов высших порядков;

‒ аппроксимации и определению закона распределения величин .

Анализ условий функционирования систем поиска и систематизации текстов показал, что минимально возможным размером алфавита, которым задается словарь ключей, является 43 [5]. В этой связи размером доверительного интервала будет выступать значение мощности алфавита. Ошибка репрезентативности (погрешности оценки) статистических характеристик узла префиксного дерева определяется как 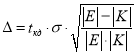, где — коэффициент доверия, определяемый по таблице Лапласа как , D — доверительная вероятность (точность) выборки, — дисперсия распределения вероятностей заполнения структуры данных префиксного дерева, — мощность множества значений элементов таблицы состояний и переходов (размер генеральной совокупности), — мощность алфавита ключевых слов (размер выборки для оценки параметра). Тогда учитывая, разреженность матрицы префиксного дерева, мощность множества значений элементов таблицы состояний и переходов для количества ключевых слов будет определяться как . Определим погрешность формирования характеристического вектора для минимальной мощности алфавита с уровнем точности 0,95. Экспериментальная оценка показала, что в среднем дисперсия распределения вероятностей заполнения структуры данных для словаря ключевых слов составляет 0,14. Таким образом при длине выборки 43 для оценки статистических параметров погрешность составит 11,23 %, что приемлемо для дальнейшего использования вычисленных оценок в процедуре классификации узлов СДПД.

Проведение эксперимента по исследованию эффективности количества моментов высших порядков в модели структуры данных префиксного дерева заключалось в измерении коэффициента уплотнения таблицы в различные промежутки времени. Под промежутками в ходе исследований понимается количество этапов уплотнения — итераций составления списков пар узлов-кандидатов на совмещение с последующим переформированием таблицы. В дальнейшем составлялись графики роста коэффициента уплотнения со временем работы процедуры для каждого из набора моментов высших порядков, задаваемых статистической моделью. Исследовались следующие наборы моментов высших порядков: , , , , и , т. е. . В силу использования для дальнейшей разработки алгоритма уплотнения положений теории распознавания образов назовем исследуемые наборы характеристическим вектором. Исходными данными для проведения эксперимента выступил список ключевых слов объемом в .

В результате эксперимента выявлен оптимальный размер характеристического вектора (набор моментов высших порядков) D = 4 относительно максимально быстрого достижения требуемого коэффициента уплотнения, равного 0,9.

Опишем условия проведения эксперимента по выявлению статистических характеристик структуры данных префиксного дерева. В ходе аппроксимации закона распределения случайной величины , анализу подверглись 200 таблиц, описывающих префиксное дерево, для обработки словаря объемом порядка строк. Первоначальный вид распределения значения индекса представлен гистограммой на рисунке 1, мощность алфавита = 43.

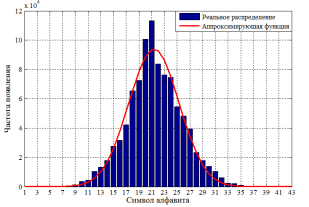
Очевидно, что в таком представлении распределение не может быть описано ни одним из известных законов. Следует отметить, что на эффективность алгоритма «лучевого» поиска не влияет порядок расстановки как символов алфавита, так и столбцов структуры префиксного дерева. Выводы, полученные в результате анализа построения префиксного дерева для алгоритма «лучевого» поиска, позволяют провести процедуру упорядочивания частотности появления символов в словаре ключей. Данный факт позволяет выбрать такую расстановку символов и столбцов, а равно и случайной величины , которая позволяет описать ее распределение одним из известных законов. Это означает, что будет изменен порядок вхождения символов алфавита в структуру префиксного дерева, причем без нарушения общности функционирования самого алгоритма «лучевого» поиска. Таким образом в ходе экспериментальных исследований строки таблицы префиксного дерева переупорядочивались в порядке убывания частотности от начала (рис. 2, а) и от середины (рис. 2, б) алфавита.

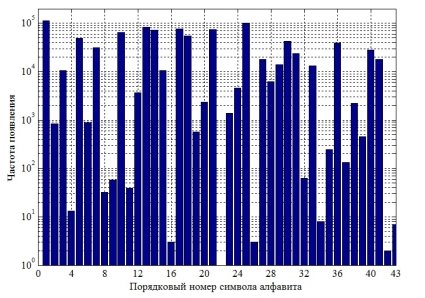
Рис. 1. Гистограмма распределения случайной величины Ind

Становится очевидным, что в таком упорядоченном виде распределение случайной величины Ind может быть аппроксимировано одним из известных законов, например, экспоненциальным (рис. 2, а) или нормальным (рис. 2, б).

В качестве инструмента анализа кривых была использована среда MatLab, позволяющая найти приближение закона распределения случайной величины [6]. Аппроксимация экспериментальных данных стандартными параметрическими моделями (кривыми) производится с оценкой качества приближения как графически, так и с использованием различных критериев пригодности приближения: SSE (сумма квадратов ошибок), R-square (критерий R-квадрат), AdjustedR-square (уточненный R-квадрат), RSME (корень из среднего квадрата ошибки).

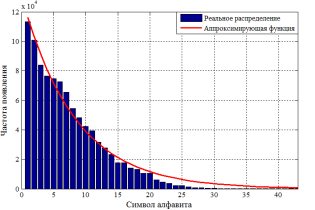
а) б)

Рис. 2. Гистограмма распределения переупорядоченной случайной величины Ind: а) в порядке убывания от начала алфавита; б) в порядке убывания от середины алфавита

Проведенные экспериментальные исследования показали, что анализируемое распределение в большей близости аппроксимируется нормальным законом по сравнению с экспоненциальным. В дополнение к этому эмпирическое распределение подверглось проверке гипотезы на нормальное распределение по критерию согласия Пирсона [7]. Значения критерия χ² показали подтверждение гипотезы с достоверностью ≈ 0,92.

Условия эксперимента обеспечивают достаточную достоверность и точность аппроксимации и определения параметров распределения символов алфавита, используемого для описания словарей ключевых признаков и формирования СДПД.

Приближение распределения вероятностей дискретной случайной величины непрерывной функцией правомерен в силу центральной предельной теоремы [8], например для биномиального закона увеличение количества дискретных случайных величин дает основание считать биномиальное распределение нормальным с параметрами математического ожидания np и дисперсии npq: Bin(n, p) ≈ N(np, npq).

Для дискретной случайной величины общая формула, задающая производящую функцию моментов, принимает вид:

(5)

В силу аппроксимации значения индекса нормальным законом распределения, а также представлением структуры префиксного дерева моментами случайной величины, определим производящую функцию моментов:

(6)

где и — математическое ожидание и дисперсия соответственно. Задание вероятностного распределения индекса узла префиксного дерева производящей функцией моментов обусловлено удобством вычисления моментов соответствующего порядка:

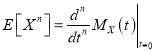, (7)

где — момент n-го порядка.

Таким образом, в результате проведенных исследований, аналитическая модель СДПД словаря ключей принимает следующий вид:

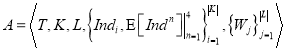, (8)

где

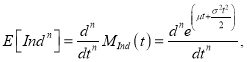(9)

как следствие выражения (6).

Модель структуры данных префиксного дерева (8) определяет общий центр статистического пространства, на котором определена таблица словаря. В этой связи, на основании утверждения (1) приведем утверждение: свойство совместимости узла префиксного дерева будет определять мера удаленности от статистического центра вектора, представленного вероятностными характеристиками столбца-кандидата. В свою очередь мера удаленности по каждой из координат характеристического вектора, описывающего узел префиксного дерева есть не что иное, как смещение оценки параметра случайной величины:

(10)

— параметры распределения, — статистические оценки четырех первых моментов случайной величины j-го узла префиксного дерева.

Введение понятия меры удаленности от центра столбца СДПД, представленного характеристическим вектором, обусловливает необходимость использования определенной метрики. Ввиду своей простоты и эффективности наибольшее распространение получила метрика Евклида. Однако ее использование в задачах теории классификации образов определено рядом условий, одним из которых является отсутствие корреляции между признаками объекта (элементами характеристического вектора). Согласно метода главных компонент или преобразования Карунена–Лоэва, одной из решаемых им задач является: построение для заданной случайной величины такого ортогонального преобразования координат, в результате которого корреляции между отдельными координатами обратятся в нуль. Для решения этой задачи успешно применяется сингулярное разложение матриц (singularvaluedecomposition, SVD) [9]. Сингулярным разложением матрицы M порядка m×n является разложение следующего вида: где — матрица размера m×n с неотрицательными элементами, у которой элементы, лежащие на главной диагонали — это сингулярные числа (а все элементы, не лежащие на главной диагонали, являются нулевыми), а матрицы U (порядка m) и V (порядка n) — это две унитарные матрицы, состоящие из левых и правых сингулярных векторов соответственно, а V* — это сопряженно-транспонированная матрица к V. В дополнение к сингулярному разложению матриц характеристических векторов для удобства представления и визуализации векторного пространства необходимо провести нормирование смещений оценки параметра случайной величины (10): 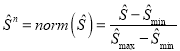, где и — максимальные и минимальные значения смещений оценки каждого из моментов. Тогда с учетом вышесказанного, множество характеристических векторов, описывающих СДПД примет окончательный вид:

. (11)

Следует отметить, что нормальное распределение индекса СДПД дает дополнительное полезное, с точки зрения эффективности алгоритма уплотнения, свойство, заключающееся в бесконечной делимости [8]. Нормальное распределение является бесконечно делимым. Если случайные величины и независимы и имеют нормальное распределение с математическими ожиданиями и и дисперсиями и соответственно, то также имеет нормальное распределение с математическим ожиданием и дисперсией . Отсюда вытекает, что нормальная случайная величина представима как сумма произвольного числа независимых нормальных случайных величин.

Подобное свойство дает основание для использования в ходе уплотнения СДПД процедуры объединения нескольких индексов в одну анализируемую случайную величину. Такой прием позволяет сократить общее время работы алгоритма уплотнения за счет введения этапности и уменьшения количества рассматриваемых индексов на каждом этапе в несколько раз.

В результате статистического моделирования была разработана адекватная модель структуры данных префиксного дерева с позиции процедуры уплотнения, концептуальная схема которой представлена на рисунке 3.

Исходными данными модели являются:

‒ Т — словарь искомых ключевых словарных признаков в обрабатываемых текстах;

‒ — количество слов-признаков, используемых при обработке текста;

‒ К — алфавит описания слов-признаков.

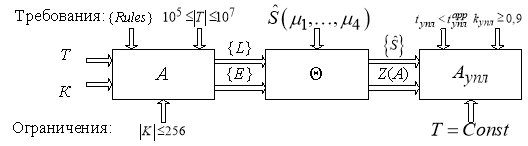
Рис. 3. Концептуальная схема аналитической модели СДПД

В роли целевой функции выступает представление такого функционала преобразования структуры данных А, что выполняется условие:

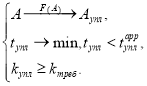
К модели предъявляются следующие требования:

‒ структура данных префиксного дерева формируется согласно множества правил построения признаковых таблиц для алгоритма «лучевого» поиска»;

‒ размер словаря ключей лежит в пределах ;

‒ узлы префиксного дерева в модели представляются в виде множества декоррелированных нормированных смещенных статистических оценок ;

‒ время уплотнения СДПД должно быть меньше, чем используемое известными аппроксимирующими алгоритмами ;

‒ коэффициент уплотнения должен быть не менее требуемого .

Модель функционирует в условиях следующих ограничений:

‒ мощность алфавита представления признакового словаря не превышает 256;

‒ в ходе процесса уплотнения структура словаря остается неизменной: .

Операторное представление аналитической модели СДПД для процедуры ее уплотнения задается следующими выражениями:

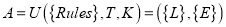1. — формирование начальной СДПД на основе множества правил построения таблицы префиксного дерева 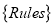, словаря признаков Т, описываемого алфавитом К. По исполнению оператора U структура А представляет собой множество множества узлов префиксного дерева 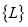и множества значений элементов таблицы состояний и переходов .
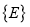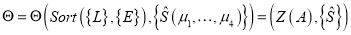2. — вычисление параметров статистического распределения структуры А, после проведения процедуры сортировки Sort(x) узлов префиксного дерева, а также получение статистических оценок 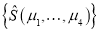параметров распределения значений элементов таблицы состояний и переходов 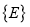для каждого узла из 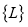. Результатом выполнения оператора является 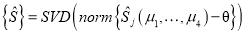множество декоррелированных нормированных смещений оценок распределения случайной величины Ind, а также 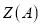— функционал процедуры совмещения узлов СДПД.
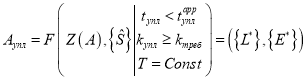3. – формирование уплотненной СДПД, состоящей из множества реструктурированных узлов 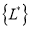и множества значений элементов таблицы состояний и переходов 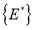, в условиях введенных требований и ограничений.

Объединяя описанные выше преобразования, операторная форма аналитической модели СДПД в общем виде примет вид:

.

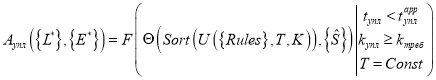Итак, в статье при моделировании СДПД были определены ее статистические характеристики, влияющие на эффективность процедуры уплотнения. Адекватность разработанной аналитической модели подтверждается утверждением о вероятности совместимости столбцов и ее следствием. В дополнение к этому, гипотезу исследования подтверждают и экспериментальные данные, которые в достаточной мере согласованы с теоретическими следствиями. Разработанная концептуальная схема модели позволяет отразить в операторной форме статистическую сущность таблицы состояний и переходов префиксного дерева с позиции ее уплотнения. В результате аналитическая модель структуры данных префиксного дерева формирует признаковое пространство числовых характеристик битовых карт для системы классификации столбцов на совместимость. Отличительной особенностью модели является учет статистических характеристик структуры данных префиксного дерева в процессе ее уплотнения.

Литература:

1. Кнут, Дональд Э. Искусство программирования, том 3. Сортировка и поиск, 2-е изд.: Перевод с английского: учебное пособие / Д. Э. Кнут. — М.: Издательский дом «Вильямс», 2000. — 832 с.
2. Марьянов, П. А. Об уплотнении структуры данных префиксного дерева в условиях большой разветвленности узлов / П. А. Марьянов, А. Ю. Куликов, А. Л. Кузьмин // Вестник науки. Сборник научных работ преподавателей, аспирантов, магистрантов и студентов физико-математического факультета. Вып. 12. — Орел: ФГБОУ ВПО «ОГУ», 2013. — С.122–124.
3. Марьянов, П. А. Способы поиска информации при условии большого количества ключевых слов / П. А. Марьянов, А. Ю. Куликов // Вестник науки. Сборник научных трудов. — Орел: ФГБОУ ВПО «ОГУ», 2012, С. 99–102.
4. Вентцель, Е. С. Теория случайных процессов и ее инженерные приложения: учеб. пособие для втузов / Е. С. Вентцель, Л. А. Овчаров — 2-е изд., стер. — М.: Высш. шк., 2000. — 383 с.
5. Марьянов, П. А. Распределение элементов в структуре данных префиксного дерева в условиях применения с большим объемом ключевых слов / П. А. Марьянов, К. Г. Масленников, С. В. Морковин // Территориально распределенные системы охраны: научный сборник № 6. Ч. 1 (2–4 апреля 2013 г., Калининград). — Калининград: Калининградский пограничный институт ФСБ России, 2013. — С. 156–158.
6. Иглин, С. П. Математические расчеты на базе MatLab / С. П. Иглин. — СПб.: Питер, 2005. — 376 с.
7. ГОСТ Р. 50.1.033–2001. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть 1. Критерии типа хи-квадрат. — Введ. 2001. — Москва: ФГУП «Стандартинформ». — 87 с. (Рекомендации по стандартизации).
8. Гмурман, В. Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В. Е. Гмурман. — 4-е изд., доп. — М.: Высшая школа, 1972. — 368 с.
9. William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. 2.6 Singular Value Decomposition // Numerical Recipes in C. — 2nd edition. — Cambridge: Cambridge University Press. — ISBN 0–521–43108–5.