Рефракция света — атмосферно-оптическое явление, вызываемое преломлением световых лучей в атмосфере и проявляющееся в мнимом смещении удалённых объектов, а также в изменении их формы. При решении геодезических и астрономических задач, влияние рефракции света на конечный результат пытаются устранить использованием улучшенных оптических систем, изменением внешних условий среды или математическими методами путем введения поправок. Степень атмосферной рефракции зависит от температуры и давления, а также влажности (количества водяного пара, что особенно важно при наблюдении в середине инфракрасной области спектра). Предложен математический метод уменьшения влияния рефракции при наблюдении Солнца. Использование этого метода повышает точность определения широты и дает возможность производить наблюдения в любое время за счет устранения редукции на меридиане.
Ключевые слова: астрономическая рефракция, широта по Солнцу; итеративные приближения; редукция на меридиане; часовой угол; параллактический треугольник; астрономическая геодезия
В настоящее время вопрос независимого определения координат точек на земной поверхности является важной проблемой в геодезии. Знание широты и долготы места необходимо для определения геодезических координат точек, для привязки геологических месторождений, профилей скважин. Поэтому перед исполнителем работ встает задача высокоточного определения астрономических координат.Задача повышения точности астрономических определений ставилась многими учеными [1–4]. Решение этой задачи возможно за счет лучшего учета влияния атмосферы [5–6], совершенствования методики обработки астрономических определений и разработки новых способов и методик определений [7–8], внедрения новых технологий при астрономических определениях [9]. Для устранения дисперсии корректировку преломления света в атмосфере производят парой вращающихся стеклянных призм. Кроме повышения точности, большое значение имеет и повышение производительности астрономических определений. Этому способствует появление принципиально новых технических средств наблюдений и новых способов астрономических определений [10].
Астрономическая рефракция вносит наибольшее влияние на результат измерений, так как является отклонением световых лучей от прямой линии при прохождении ими атмосферы из-за изменения плотности воздуха с высотой. Атмосферная рефракция около земной поверхности создаёт миражи и может приводить к тому, что далекие объекты будут казаться мерцающими, дрожащими, находящимися выше или ниже своего истинного положения. Кроме того, форма объектов может быть искажена — они могут казаться сплюснутыми или растянутыми. Рефракция влияет не только на световые лучи, но и на всё электромагнитное излучение, хотя и в разной степени. Например, в видимом свете, синий цвет больше подвержен воздействию рефракции, чем красный. Это может приводить к тому, что астрономические объекты расплываются в спектр на изображениях с высоким разрешением. Атмосферная рефракция увеличивает ошибки конечного результата сильнее всего тогда, когда она не является однородной, например, при наличии турбулентности в воздухе. А также влияет на точность определения поправки за редукцию на меридиане, что приводит к повышению погрешности определения широты.
Целью работы является реализация математического метода по уменьшению влияния астрономической рефракции на примере вычисления широты места по Солнцу в программной среде VBA. На основе уравнений сферической тригонометрии из параллактического треугольника было выведено уравнение (1), связывающие зенитное расстояние, склонение, часовой угол и широту места. Достоинством данного метода является возможность производить наблюдения в удобное время без учета редукции на меридиане.
Методика определения широты по зенитальным наблюдениям Солнца подробно описана в [1]. Дуги меридиана наблюдателя, круга склонений и вертикала светила образуют на сфере (рисунок 1) параллактический треугольник с вершинами в Полюсе мира Р, зените Z и месте светила σ.
Параллактический треугольник связывает между собой горизонтные и экваториальные координаты светила с географическими координатами места наблюдения. Применяя к этому треугольнику основные формулы сферической тригонометрии можно вывести уравнение (1).
![]() (1)
(1)
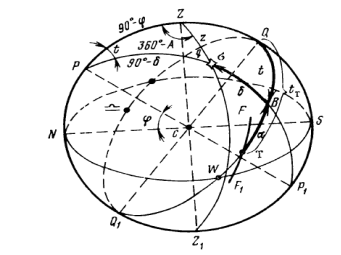
Рис. 1. Небесная сфера с центром в пункте К
Зная склонение δ, часовой угол tи предварительное значение широты φ0, и решив уравнение (1), можно получить точное значение широты места φ без учета влияния ошибки определения поправки за редукцию на меридиане. Сложность решения уравнения (1) заключается в том, что искомая переменная φ присутствует в функции косинус и синус, что затрудняет использование стандартных методов решений уравнений. Для решения уравнения (1) был предложен численный метод последовательных приближений, реализованный в программной среде VBA. Интерфейс программы расчета показан на рисунке 2.
В случае если наблюдатель неправильно определил время в одном из приемов или некорректно взял отсчет по тахеометру, в значении широты этого приема присутствует грубая ошибка. При расчете среднего значения широты, это ошибка окажет влияние на точность полученного результата. В программе предусмотрена возможность отбраковать прием, в котором введены некорректные данные и для сохранения результатов расчетов, в программе Microsoft Excel создается журнал астрономических наблюдений (рис. 3).
Экспериментальные данные, обработанные для расчета широты с использованием указанной программы совпадают с результатами, полученными по стандартному методу [1].
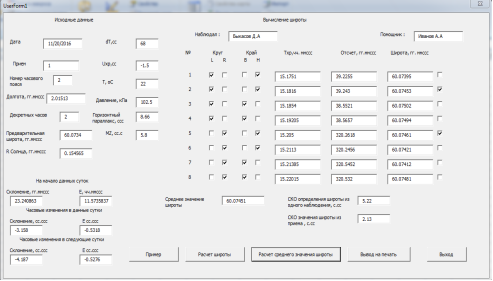
Рис. 2. Интерфейс программы
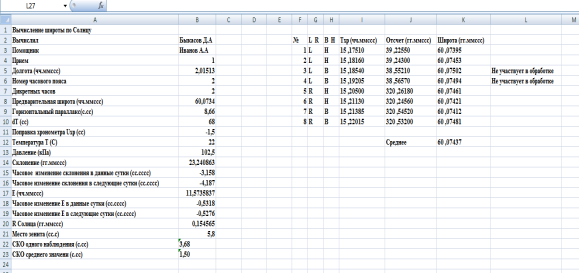
Рис. 3. Журнал астрономических наблюдений
Использование программных средств vba позволяет решать данную задачу новым методом без учета редукции, что способствует снижению ошибки определения широты вызванной астрономической рефракцией увеличить производительность выполнения работ.
Литература:
- И. С. Пандул. Астрономические наблюдения по Солнцу. — М.: -Недра,1983. — 128 с.
- Машимов М. М. Высшая геодезия. — М.: ВИА, 1991. — 552 с.
- Уралов С. С. Современные проблемы геодезической астрономии // Исследования по геодезии, аэрофотосъемке и картографии. — М.: МИИГАиК, 1978. — С. 4–9.
- Глазунов А. С. О повышении точности полевых астрономических измерений // ГЕО-Сибирь-2005. Науч. конгр.: сб. материалов в 7 т. (Новосибирск, 25–29 апреля 2005 г.). — Новосибирск: СГГА, 2005. Т. 2. — С. 79–83.
- Василенко Н. А. Исследование аномалий астрономической рефракции: автореферат на соиск. учен.степ. канд. физ. мат. наук. — Л., 1977. — 15 с.
- Кононович Э. В., Мороз В. И. Общий курс астрономии. М.: Едиториал УРСС. 544 с. 2004
- Глазунов А. С., Кузьмин М. И. Определение широт по способу Талькотта с наблюдением звезд вне меридиана // Тр. II Орлов.конф. «Изучение Земли как планеты методами геофизики, геодезии и астрономии». — Киев: Наукова Думка, 1988. — С. 217–218.
- Глазунов А. С. Обоснование комбинированного разностно-зенитального способа определения широты // Вестник СГГА. — 1998. — № 3. — С. 43–46.
- Status of Geodetic Astronomy at the Beginning of the 21st Century [Электронный ресурс] / C. Hirt, B. Bürki. — Режим доступа: http://www.ife.uni-hannover.de/mitarbeiter/seeber/ seeber_65/pdf_65/ hirt8.pdf
- Глазунов А. С., Голдобин Д. Н., Коршиков В. В. Полевой астрономический оптико-электронный комплекс // ГЕО-Сибирь-2007. III Междунар. науч. конгр.: сб. материалов в 6 т. (Новосибирск, 25–27 апреля 2007 г.). — Новосибирск: СГГА, 2007. Т. 2, ч. 2. — С. 79–83.







