В статье рассказывается о понятии интегральной и дифференциальной нелинейности, необходимостей их измерения при проверке аналого-цифровых преобразователей и приводится алгоритм измерения интегральной и дифференциальной нелинейностей для аналого-цифровых устройств.
Ключевые слова: аналого-цифровой преобразователь, интегральная нелинейность, дифференциальная нелинейность
Интегральная нелинейность (INL — integral non-linearity) − это погрешность, которая вызывается отклонением линейной функции передаточной характеристики АЦП от прямой линии. Обычно передаточная функция с интегральной нелинейностью аппроксимируется прямой линией по методу наименьших квадратов. Часто аппроксимирующей прямой просто соединяют наименьшее и наибольшее значения. Интегральную нелинейность определяют путем сравнения напряжений, при которых происходят кодовые переходы. Для идеального АЦП эти переходы будут происходить при значениях входного напряжения, точно кратных LSB (Least Significant Bit). А для реального преобразователя такое условие может выполняться с погрешностью. Разность между «идеальными» уровнями напряжения, при которых происходит кодовый переход, и их реальными значениями выражается в единицах LSB и называется интегральной нелинейностью [1].
У идеальной передаточной характеристики АЦП ширина каждой «ступеньки» должна быть одинакова. Разница в длине горизонтальных отрезков этой кусочно-линейной функции из ![]() , где
, где ![]() — разрядность АЦП, «ступеней» представляет собой дифференциальную нелинейность (DNL − differential non-linearity) [1].
— разрядность АЦП, «ступеней» представляет собой дифференциальную нелинейность (DNL − differential non-linearity) [1].
Величина наименьшего значащего разряда у АЦП составляет:
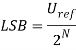
Разность напряжений между каждым кодовым переходом должна быть равна величине LSB. Отклонение этой разности от LSB определяются как дифференциальная нелинейность [1].
Перед описанием алгоритма введем следующие обозначения:
|
Fin |
Частота входного сигнала; |
|
DCin |
Величина постоянной составляющая входного синусоидального сигнала; |
|
ACin |
Величина переменной составляющая входного синусоидального сигнала (амплитуда); |
|
Npt |
Количество точек оцифрованного сигнала; |
|
Hi |
Число выпадений кода i в массиве выходных данных АЦП; |
|
Vo |
Ошибка смещения АЦП; |
|
G |
Ошибка усиления АЦП; |
|
DNLi |
Дифференциальная нелинейность для кода i; |
|
INLi |
Интегральная нелинейность для кода i. |
Для начала необходимо подать на вход АЦП с генератора синусоидальный сигнал со следующими характеристиками:
![]()
где
Величина постоянной составляющая входного синусоидального сигнала равняется:
![]()
Перед тем как вычислять частоту входного сигнала, требуется вычислить необходимое число точек оцифрованного сигнала:
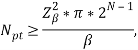
где ![]() - точность вычисляемого параметра;
- точность вычисляемого параметра;
![]() - квантиль нормального распределения.
- квантиль нормального распределения.
Частота входного сигнала:
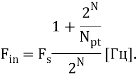
С помощью тестера Advantets V93000 PS1600 с выхода АЦП мы собираем массив точек оцифрованной синусоиды. Массив должен содержать целое число периодов оцифрованной синусоиды.
Обработку массива оцифрованной синусоиды и вычисление интегральной и дифференциальной нелинейностей будем проводить с помощью программного пакета Matlab.
Для начала необходимо для массива выходных данных АЦП построить гистограмму. То есть найти зависимости частоты появления кода
H = histo(samples,0:1:power(2,N)-1);
Далее необходимо вычислить напряжение перехода уровней АЦП (![]() — напряжение перехода из
— напряжение перехода из ![]() в
в ![]() ):
):
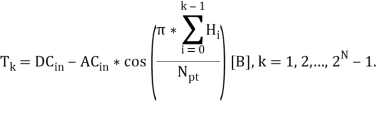
Листинг кода для вычисления характеристики преобразования:

Для вычисления интегральной и дифференциальной нелинейностей необходимо вычислить ошибок усиления и смещения АЦП. Формула для расчёта ошибки усиления:
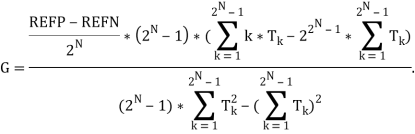
Формула для вычисления ошибки смещения АЦП:
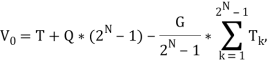
где ![]() — значение соответствующее идеальному переходу выходного кода АЦП из 0 в 1.
— значение соответствующее идеальному переходу выходного кода АЦП из 0 в 1.
Листинг кода для вычисления ошибок усиления и смещения АЦП:

Вычисление интегральной и дифференциальной нелинейностей проводилась с помощью методику IEEE Standard for Terminology and Test Methods for Analog-to-Digital Converters. Согласно этой методике формула для вычисления интегральной нелинейности [2]:
![]()
Формула для вычисления дифференциальной нелинейности методом IEEE Standard for Terminology and Test Methods for Analog-to-Digital Converters [2]:
![]()
Листинг кода для вычисления интегральной и дифференциальной нелинейностей методом IEEE Standard for Terminology and Test Methods for Analog-to-Digital Converters:

Литература:
- Шишов О. В., Аналого-цифровые каналы микропроцессорных систем управления: учебное пособие [Текст] / О. В. Шишов. — М.: Берлин: Директ-Медиа, 2015. — 211 с.;
- IEEE Standard for Terminology and Test Methods for Analog-to-Digital Converters. [Текст] − IEEE Standard, 2009. — 128 с.







