В настоящее время обработкой звукового сигнала занимаются множество специалистов: инженеры, звукорежиссеры, звукооператоры, музыканты. Все они преследуют цель синтеза звукового сигнала и (или) изменения параметров ЗС для выполнения инженерных (например, применение кодеков для сжатия звуковых сигналов) и художественных (например, улучшение звучания композиции путем тщательной настройки отдельных частот) задач.
Существует множество аппаратных и программных средств для синтеза и обработки звукового сигнала. Существует как платное ПО (Adobe Audition), так и бесплатное ПО (Audacity, Sonic Visualizer) для работы со звуком. Ядром (математической основой) данных программных средств является дискретное преобразование Фурье, а также его частный случай — быстрое преобразование Фурье. Кроме этого, используются различные особенности и свойства преобразования Фурье, например, симметричность, заполнение нулями, смещение.
Цель.
Подробно разобрать дискретное преобразование Фурье, быстрое преобразование Фурье, а также свойства преобразования Фурье, используя программную реализацию. Написать скрипт на Python, позволяющий осуществлять преобразование Фурье для получения графиков с помощью которых можно проводить анализ звуковых сигналов.
Результат работы.
Была осуществлена программная реализация свойств преобразования Фурье в Python.
Будем использовать «ipython», который представляет собой оболочку, которая очень удобна для интерактивного вызова команд python. Также используем «matplotpib» (для импорта при старте ipython пишем в терминале: «ipython-pylab»). Скрипт всё же удобно набирать в текстовом редакторе. В данном случае мы используем уже знакомый нам пакет «numpy», а также пару новых: треугольная функция (triang из scipy.signal) и реализацию дискретного преобразования Фурье в python (fft из scipy.fftpack). Если длина последовательности fft не будет равна 2n то вместо быстрого преобразования Фурье (fft) будет выполняться дискретное преобразование фурье (dft). Именно таким образом работает эта команда. Выполнив преобразование Фурье последними двумя строками кода получаем частотную и фазовую характеристики. Данная программа не выводит сразу никаких графиков, она считает все переменные. Построить графики можно вводя, например:
plot(x) — выводит входную функцию (треугольник)
plot(X) — выводит график преобразования Фурье
plot (mX) — выводит график частотного спектра
plot (pX) — выводит график фазового спектра
Рассмотрим график частотного спектра треугольного сигнала (рисунок 1). Он симметричен вокруг нулевого отсчета. Первая часть — это положительные значения (до 8 отсчета), а вторая часть — отрицательные. Это значит, что четырнадцатый отсчет является по факту также отсчетом минус первым. Данный график очень ясно дает понять ранее описанное свойство ДПФ — симметричность.
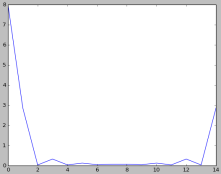
Рис. 1. Частотный спектр треугольного сигнала
Построив частотный спектр, мы видим, что он не равен нулю, хотя он должен быть таковым. Дело всё в том, что треугольная функция не центрована относительно нуля. Исправим это, внеся некоторые корректировки в исполняемый скрипт, а именно добавим буфер быстрого преобразования Фурье (тот самый буфер о котором я писал в свойствах преобразования Фурье):
− fftbuffer=np.zeros(15) — создаем буфер, заполненный нулям;
− fftbuffer [:8]=x [7:] — перемещаем конец треугольного сигнала в первую часть буфера;
− fftbuffer [8:]=x [:7] — перемещаем начало треугольного сигнала в последнюю часть буфера;
− X=fft(fftbuffer) — считаем преобразование Фурье буфера, заполненного значениями функции треугольника.
Построив график фазового спектра треугольника (который теперь расположен от -7 до 7) мы получаем симметричный график, который и должен был получиться (значения на рисунке в -15 степени, что очень близко к нулю) (рисунок 2):
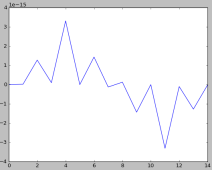
Рис. 2. Частотный спектр треугольной функции
Теперь, используя практически тот же скрипт, но с добавлением функции чтения звуковых файлов, посчитаем преобразования Фурье реального звукового сигнала.
В файл скрипта заносим изменение в виде добавления функции «wavread», которая рассматривалась ранее в других скриптах, а также добавляем код, позволяющий центрировать звуковой файл. Таким образом получим скрипт, который выполняет ДПФ и БПФ:

Рис. 3. Скрипт, позволяющий осуществлять ДПФ с целью получения частотной и фазовой характеристики реального сигнала
Команды библиотеки «matplotlib» (plot(x) — построить форму сигнала, plot(x1) — построить выбранную для анализа часть сигнала) позволяют получить графики, которые необходимы нам для анализа. Например, после выполнения скрипта, запросим фазовую и частотную характеристики, введя plot(mX) и plot(pX). Также, чтобы визуализировать свойство заполнения нулями мы можем построить ДПФ буфер, используя plot(fftbuffer). На рисунке 4 приведены построенный с помощью скрипта python графики, демонстрирующие сразу несколько свойств преобразования Фурье — симметричность (на частотной характеристике и фазовой) и заполнения нулями (на графике буфера ДПФ).
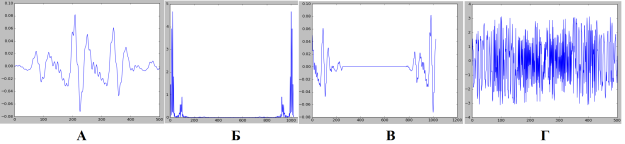
Рис. 4. а) фрагмент ЗС, б) частотный спектр (включая положительную и отрицательную части), в) буфер ДПФ, г) фазовый спектр
Чтобы фазовый спектр был более читаем, применим развертывание фазы. Для этого изменим строку с расчетом фазовой характеристики:
pX=np.unwrap(np.angle(X))
И построим фазовую характеристику. Рисунок 5 изображает фазовую характеристику нашего входного сигнала в удобном для анализа виде.
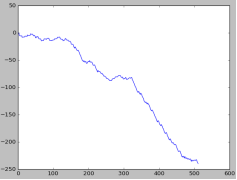
Рис. 5. Фазовая характеристика звукового сигнала
Таким образом удалось реализовать несколько свойств и теорем Фурье в виде Python скрипта, чтобы лучше понять концепции симметрии, заполнения нулями, развертывания фазы. Данный скрипт позволяет выполнять Фурье анализ фрагмента звукового сигнала.
Литература:
- Официальный сайт Соник Визуализатор для скачивания и получения документации. Режим доступа: http://www.sonicvisualiser.org/
- Официальный сайт проекта Audacity для скачивания и получения документации. Режим доступа: http://www.audacityteam.org/
- Официальный сайт пакета iPython. Режим доступа: http://www.ipython.org/
- Электроакустика и звуковое вещание: Учебное пособие для вузов / Э. И. Вологдин, А. П. Ефимов, А. А. Фадеев, И. А. Алдошина, Г. П. Катунин, Л. Н. Кацнельсон, Ю. А. Ковалгин — 2007. – 872c.
- Цифровая обработка сигналов в трактах звукового вещания: Учебное пособие для вузов / О. Б. Попов, С. Г. Рихтер — 2007. – 341 с.
- Акустика: Справочник / А. П. Ефимов, А. В. Никонов, М. А. Сапожников, В. И. Шоров — 1989. – 336 с.
- Сайт Wikipedia. Discrete Fourier Transform. Режим доступа: https://en.wikipedia.org/wiki/Discrete_Fourier_transform
- Сайт Wikipedia. Fast Fourier Transform. Режим доступа: https://en.wikipedia.org/wiki/Fast_Fourier_transform
- Официальный сайт компании National Instruments предоставляющей платформы для проведения исследований, а также программный продукт LabVIEW. Режим доступа: http://www.ni.com/ru-ru.html







