Одним из факторов, влияющих на скорость развития науки, является её популяризация. На данный момент, большинство методов популяризации науки — это в основном книги, научно-популярные журналы или видеоролики, однако главным недостатком таких методов является отсутствие какой-либо интерактивности.
Намного большего эффекта можно достичь, если в целях популяризации применять интерактивные приложения, где пользователь имеет возможность взаимодействовать с виртуальной средой, наблюдать последствия своих действий и приходить к различным выводам, используя метод проб и ошибок.
Таким образом возникла идея разработки проекта, в котором будут реализованы различные симуляции физических законов и явлений, а также интерфейс, который позволит в интерактивной форме ознакомить пользователя с некоторыми особенностями различных научных профессий.
Ключевые слова: алгоритмы оптимизации
Одной из первых задач с которой пришлось столкнуться при разработке интерактивного симулятора, это необходимость разработки специальных методик для работы с огромными числами для измерения размеров космических объектов и расстояний между ними.
Так как в космосе все находится на огромной дистанции, возникает проблема снижения точности расчетов при работе с числами с плавающей точкой.
Данное явление широко известно и именуется floating point precision.
В 3-х мерной графике, каждый объект имеет свою координату, в которой он расположен, не смотря на то что в используемой интегрированной среде разработке (Unity3D) нет фиксированных ограничений на максимальную дальность расположения объекта от центра координат, тем не менее нельзя обычным способом расположить планету в нужной координате.
Например, если в центр координат расположить Солнце, то Землю придется разместить на расстоянии 150000000000 метров от Солнца.
Проблема заключается в том, что для описывания координат применяется тип переменной «Vector3», который в свою очередь состоит из 3х переменных типа float для осей X, Y, Z.
Float это 32х битное значение которое имеет свойство снижения точности вычислений по мере удаления значения от 0. Float способен содержать числа с точностью 8 знаков включая точку. Например, числа 1.234567 или 123456.7 могут обсчитываться без потерь точности. Однако если попытаться выполнить операцию 12345678 + 0.1 то результат будет не 12345678.1, а все так-же 12345678, потому что новое значение выходит за пределы возможностей float.
Это причина, по которой нельзя разместить планету в координате 150 000 000 000, потому что при движении вокруг Солнца, она либо не будет двигаться, либо ее скорость движения будет не точной.
Однако существует метод, позволяющий получить требуемый результат, не выходя за пределы диапазона вычислений.
Метод заключается в том, чтобы для расчетов движения космических объектов, применять тип переменной double, это 64-х битный аналог float, который имеет точность не 8 знаков, а 16, и способен уместить в себя всю солнечную систему с точностью до метра или сантиметра (в зависимости от желаемого размера солнечной системы).
Однако тип переменной double невозможно применять для визуализации 3D графики на экране, все видеокарты работают именно с float. А нам требуется чтобы планеты были видны с расстояния миллионы или миллиарды километров.
Обойти это ограничение позволяет тот факт, что в данном случае по мере приближения или удаления наблюдателя от планеты, меняется не расстояние до планеты, а её размер.
Рассмотрим две ситуации:
- Наблюдается шар диаметром 1 метр с расстояния 10 метров.
- Наблюдается шар диаметром 10 метров с расстояния 100 метров.
В обеих ситуациях видимый размер шара будет одинаковым. Именно этот эффект и применяется для того чтобы отображать планеты в пределах допустимых координат. Например, требуется отобразить планету, которая имеет радиус 10000000 метров и находится на расстоянии 1000000000 метров. В таком случае следует уменьшить и планету, и расстояние в 1000000 раз и отобразить небольшой шар радиусом всего 10 метров на расстоянии 1000 метров. Это допустимые величины, которые могут отображаться без потерь точности, при этом планета будет выглядеть так, как будто она расположена на расстоянии 1000000 километров от наблюдателя, что является огромным числом для визуализации обычными методами. При этом координата планеты может вообще не меняться, но изменение размера будет создавать эффект движения.
Такой эффект можно объяснить благодаря понятию «угловой размер» или «угловая величина» и формуле его расчета.
Угловой размер — это угол между прямыми линиями, соединяющими диаметрально противоположные крайние точки измеряемого (рассматриваемого) объекта и глаз наблюдателя. [1]
Именно благодаря угловому размеру объекта наблюдатель оценивает расстояние до него (при условии, что наблюдателю известен примерный размер объекта), в ином случаи оценка расстояния будет ошибочной. Но в любом случае изменение углового размера объекта обозначает факт приближения или отдаления от объекта.
Формулу углового размера можно наглядно объяснить следующем изображением:
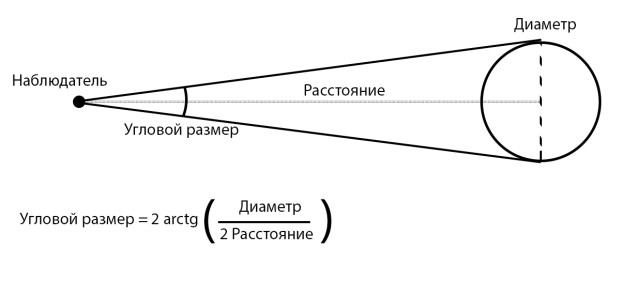
Рис. 1. Формула углового размера и её графическое представление
По формуле видно, что если значение диаметра объекта и расстояния до него будет изменяться пропорционально, то угловой размер будет оставаться неизменным.
Угловой размер определяет не величина диаметра или расстояния, а их соотношение. Таким образом, можно использовать это свойство для того чтобы визуализировать планета в пределах допустимого диапазона координат сохранив при этом ее угловой размер путем изменения масштаба планеты.
Также стоит отметить визуализацию других звездных систем и галактик, для них используется тот же тип переменных double, но так как для описания масштабов вселенной недостаточно даже диапазона double, координаты галактик задаются относительно условного центра вселенной, а координаты звезд относительно центра галактики, и соответственно координаты планет относительно звезды.
Для подтверждения целесообразности применения чисел с двойной точностью, приведем расчеты допустимых диапазонов.
При необходимой точности вычисления до 0.01 метр (1 сантиметр) и использовать float значений, максимальная удаленность от центра координат будет составлять 100000 метров (пример дробного числа 123456.78), или 100 километров. Что очень мало не только в масштабах солнечной системы, но даже в масштабах планеты.
Однако при применении double значений, максимальное удаление от центра будет достигать 10000000000000 или 10 миллиардов километров (пример дробного числа 12345678901234.56). Что равно примерно 65 астрономических единиц (одна астрономическая единица равна примерно 150 миллионов километров), а расстояние до самой дальней планеты солнечной системы, Нептуна, составляет 30 астрономических единиц. Из чего следует что применение double вычислений как раз позволяет рассчитывать движение в солнечной системе, плюс остается еще в 2 раза больше пространства при необходимости обработки еще более удаленных объектов (карликовых планет или астероидов)
При этом, когда наблюдатель выходит за пределы солнечной системы. Масштаб координат переходит на более высокий уровень, для которого минимальная точность вычислений уже составляет не 0.01 метр, а более высокое значение. И хотя при таком условии будет существовать ограничение на минимальную скорость движения наблюдателя, но 1 сантиметр в секунду слишком низкая скорость для межзвездного пространства, и она в любые случаи будет не заметна для наблюдателя.
Для расчета нового минимального предела скорости используется следующий метод. Предполагается что более высокий уровень масштаба используется для расчетов передвижения в пределах галактик, поэтому нужно определить максимально допустимый размер процедурно генерируемой галактики.
Согласно информации, из NASA/IPAC EXTRAGALACTIC DATABASE [2], самой крупной из известных галактик, является галактика IC 1101. Её диаметр составляет примерно 6000000 световых лет (для сравнения, диаметр нашей галактики «Млечный Путь» составляет 100000 световых лет). Следовательно, возьмем значение 6000000 световых лет за максимальный размер и разделим его на максимальный диапазон double значений.
6000000 / 1E+16 = 0.0000000006 световых лет, что равно примерно 5000 километров в секунду. Что и является пределом минимальной скорости движения наблюдателя в межзвездном пространстве.
И хотя эта скорость кажется невероятно большой, на самом деле наблюдатель не заметит потери точности, так как расстояние до других звезд огромно и даже при движении к ближайшей звезде, угловая величина звезды будет изменяться очень плавно, и пользователь не ощутит никаких проблем с визуализацией перемещения.
Выводы.
На основе описанного в рамках данной статьи можно заключить, что архитектура из различных координатных уровней, применение double переменных и использование свойства углового размера, позволяет создать полноразмерную вселенную, где возможен бесшовный переход наблюдателя в диапазоне от галактик до поверхности планет с точностью до сантиметра.
Литература:
- Angular diameter https://en.wikipedia.org/wiki/Angular_diameter
- NASA/IPAC EXTRAGALACTIC DATABASE http://ned.ipac.caltech.edu/cgi-bin/objsearch?objname=IC+1101&extend=no&hconst=73&omegam=0.27&omegav=0.73&corr_z=1&out_csys=Equatorial&out_equinox=J2000.0&obj_sort=RA+or+Longitude&of=pre_text&zv_breaker=30000.0&list_limit=5&img_stamp=YES







