В работе рассмотрена прочностная надежность одного из главных элементов поршневого двигателя, поршневого пальца. Проведено сравнение расчетных схем для оценки напряженно-деформированного состояния поршневого пальца. Выведены формулы для оценки изгибных напряжений в поршневом пальце.
Ключевые слова: двигатель внутреннего сгорания, поршневой палец, коэффициент запаса, прочность, метод конечных элементов
Введение: Детали поршневых двигателей, а также многие детали машин в эксплуатационных условиях подвергаются действию переменных напряжений, многократно изменяющихся во времени. Такие напряжения испытывают, например, коленчатые валы, шатуны, шатунные болты, головки цилиндров двигателей внутреннего сгорания (в том числе переменные температурные напряжения), поршневые пальцы, валики коробок скоростей, рессоры, клапанные пружины и другие детали [1].
Поршневой палец обычно рассчитывается:
‒ на прочность от изгибающих его моментов;
‒ на предельно допустимую деформацию (овализацию) во избежание заклинивания в верхней головке шатуна;
‒ на удельное давление на его трущихся поверхностях.
На поршневой палец действует максимальная нагрузка на такте впуска от сил инерции массы поршневой группы при работе на режиме максимальной частоты вращения. [2]
![]() (1)
(1)
где mпг — масса поршневой группы (без массы поршневого пальца); ωmax = (πnmax)/30 — угловая частота вращения коленчатого вала при максимально допустимой nmax; r — радиус кривошипа; λ=r/lш; lш — длина шатуна.
Кроме того, на расчетном режиме (максимального крутящего момента или номинальном) на поршневой палец на такте расширения действует нагрузка
![]() (2)где pz — максимальное давление сгорания на расчетном режиме; p0 — атмосферное давление; ω — угловая частота вращения коленчатого вала на этом же режиме.
(2)где pz — максимальное давление сгорания на расчетном режиме; p0 — атмосферное давление; ω — угловая частота вращения коленчатого вала на этом же режиме.
На рис.1 показаны основные схемы нагружения поршневого пальца, по которым можно оценить его напряженно-деформированное состояние [2].
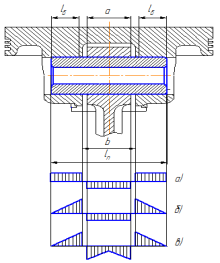
Рис. 1. Основные схемы нагружения поршневого пальца
Толстостенные пальцы наиболее чувствительны к изгибным напряжениям. Наиболее распространенные поломки в них связаны с появлением трещин в поперечном направлении, и излом начинается в среднем сечении под упрочненным слоем, от излишне высоких напряжений изгиба [3]. Поэтому важно определить, какая из схем дает наиболее достоверные результаты. Для этого выводились формулы для определения изгибных напряжений по трем расчетным схемам и рассчитывались максимальные напряжения, после чего, полученные значения сравнивались с конечно-элементным расчетом в программе ANSYS. Расчет в ANSYS проводился для максимального случая нагружения поршневого пальца, силами инерции и давлением газов.
Для вывода формул изгибных напряжений, по основным зависимостям сопротивления материала [4] строились эпюры внутренних сил и изгибающих моментов, после чего для среднего наиболее нагруженного сечения находились напряжения изгиба. При рассмотрении схемы (в), возникают сложности в установлении перепада сил между краями и центром в верхней головке шатуна. Для приближенной оценки этого перепада, использовался численный расчет, описанный ниже. В качестве результатов расчета, был получен характер распределения усилий по поршневому пальцу (рис. 2). В результате отношение сил между краями и центром принимался равным 10. Также можно заметить, что распределения усилий имеет неравномерный характер по всей длине поршневого пальца.

Рис. 2. Распределение давления в контактах, МПа
Формулы изгибных напряжений для средних, наиболее нагруженных, расчетных сечений, представлены ниже:
Для схемы а): 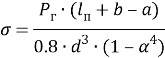 (1)
(1)
Для схемы б):
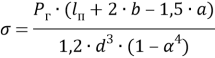 (2)
(2)
Для схемы в): 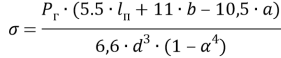 (3)
(3)
Чтобы сравнить три схемы, посчитаем по полученным формулам значения максимальных изгибных напряжений в среднем сечении поршневого пальца для трех случаев нагружения. Давление газов на такте сжатия принимается равным ![]() .
.
Параметры поршневого пальца:
Длина пальца — ![]()
Расстояние межде бобышками поршня — ![]()
Ширина шатуна — ![]()
Отношение внутреннего диаметра к наружнему — ![]()
Таким образом, получились следующие изгибные напряжения:
![]() =481,7 МПа
=481,7 МПа ![]() =412,9 МПа
=412,9 МПа ![]() =375,3 МПа
=375,3 МПа
Для сравнения аналитически полученных значений, проводился численный расчет поршневого пальца в программном комплексе ANSYS Workbench 16.2. Сначала в системе трёхмерного твердотельного проектирования Siemens NX10 создается сборка: упрощенная модель поршня, поршневой палец и верхняя головка шатуна. Затем сборка экспортируется в программу ANSYS. Далее генерируется сетка (рис.2), задаются контакты, прикладывается давление к поршню, ускорение к поршневой группе и фиксируется низ шатуна. Расчетная схема изображена на рис.3.
Рис. 3. Сетка конечных элементов поршневого пальца

Рис. 4. Расчетная схема
В качестве результата численного расчета в программе ANSYS выводится значение нормальных напряжений по оси Z (рис. 5.), значение которого можно будет сравнить с аналитически полученными значениями изгибных напряжений. Как видно на рисунке, максимальное напряжение возникает в среднем сечении и составляет 338 МПа. А аналитически полученные значения напряжений по схеме нагружения в) дают наиболее близкие значения. Погрешность аналитической формулы по схеме в) и численным расчетом составляет 9,8 %.
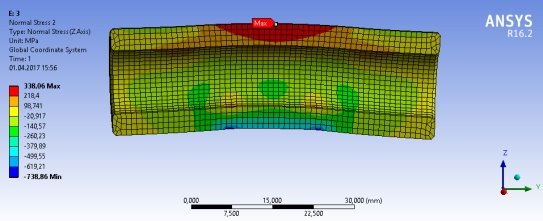
Рис. 5. Значение изгибных напряжений, при сжатии
Проведенные расчеты показали, что действительный характер распределения нагрузки неравномерный по всей длине поршневого пальца, и наиболее достоверная схем для определения напряженно-деформированного состояния пальца, соответствует схеме в). Также были выведены формулы для определения изгибных напряжений по трем расчетным схемам. Наименьшая погрешность аналитического и численного расчета, соответствует схеме в) и составляет 9,8 %.
Литература:
- Коллинз Дж. Повреждение материалов в конструкциях. Анализ, предсказание, предотвращение: Пер. с англ. — М.: Мир, 1984. — 624с.
- Гоц А. Н. Расчет на прочность при переменных напряжениях: монография. / А. Н. Гоц. — Владим. Гос. Ун-т имени Александра Григорьевича и Николая Григорьевича Столетовых. — Владимир: Изд-во ВлГУ, 2012. — 138 с.
- Конструирование двигателей внутреннего сгорания/ Н. Д. Чайнов [и др.]; Под ред. Н. Д. Чайнова. — М.: Машиностроение, 2011. — 496 с.
- Феодосьев В. И. Сопротивление материалов: Учеб. для вузов. — 10-е изд., перераб. и доп. — М.: Изд-во МГТУ им. Н. Э.Баумана, 1999. — 592с.







