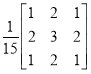Встатье рассмотрено применение сглаживающих фильтров для очистки от шума изображений в оттенках серого. В данной работе предложена новая функция для генерации масок сглаживающих фильтров. Произведено сравнение эффективности предложенных фильтров с фильтрами Гаусса. Результаты моделирования показали, что предложенный фильтр дает хороший результат очистки изображений от шума, вычислительно проще и удобней в использовании.
Ключевые слова: цифровое изображение, шум, система остаточных классов, сглаживающий фильтр, фильтр Гаусса
Методы цифровой обработки изображений широко используются на практике: в астрономии, медицине, физике, биологии, географии, археологии и т. д. [1–3] В частности, актуальна проблема очистки изображений от шума — случайного изменения значений интенсивности [4]. Некоторыми распространенными типами шума являются:
1) «соль и перец» — случайные изолированные черные или белые точки на изображении;
2) импульсный — случайные изолированные белые точки на изображении;
3) гауссов — изменении интенсивности по нормальному закону распределения.
Для улучшения качества зашумленного изображения (очистки от шума) применяют сглаживающие фильтры: простой, Гауссов, медианный, биномиальный [5,6]. В данной статье рассмотрены фильтры, которые улучшают зашумленные изображения в оттенках серого.
Предложенный метод сглаживания изображений.
Изображение представляет собой двумерную функцию![]() , где
, где ![]() и
и ![]() — это пространственные координаты, а амплитуда
— это пространственные координаты, а амплитуда ![]() в любой точке с парой координат
в любой точке с парой координат ![]() называется интенсивностью или уровнем серого цвета изображения в этой точке. Цифровое изображение состоит из конечного числа элементов, каждый из которых расположен в конкретном месте и имеет определенное значение. Эти элементы принято называть элементами изображения или пикселями. Для цифровых изображений в оттенках серого интенсивность представляется с помощью чисел без знака, изменяющимся в диапазоне от 0 до 255, с 8-битовым представлением [7–9].
называется интенсивностью или уровнем серого цвета изображения в этой точке. Цифровое изображение состоит из конечного числа элементов, каждый из которых расположен в конкретном месте и имеет определенное значение. Эти элементы принято называть элементами изображения или пикселями. Для цифровых изображений в оттенках серого интенсивность представляется с помощью чисел без знака, изменяющимся в диапазоне от 0 до 255, с 8-битовым представлением [7–9].
Предложенный нами метод сглаживания изображений обрабатывает изображение фильтром, который выглядит следующим образом:
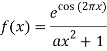 (1)
(1)
где ![]() – степень «размытия». На рисунке 1 представлен график предложенной функции. На графике видно, что функция достигает локальных максимумов в точках
– степень «размытия». На рисунке 1 представлен график предложенной функции. На графике видно, что функция достигает локальных максимумов в точках ![]() Это свойство используется в дальнейшем, при составлении масок фильтра.
Это свойство используется в дальнейшем, при составлении масок фильтра.
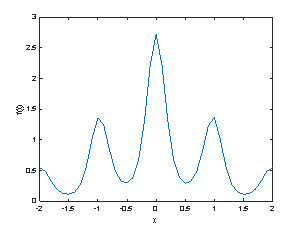
Рис. 1. График предложенной функции
Моделирование.
Моделирование производилось в математическом пакете MATLAB2015 [7]. В качестве исходных данных были взято изображение (Рисунок 2).

Рис. 2. Исходное изображение
Для искажения изображений использовался Гауссов шум с дисперсиями:![]() ,
, ![]() ,
, ![]() . Сравнивались два метода сглаживания изображений: на основе предложенной функции и с использованием фильтра Гаусса [4, 5]. Двумерная функция Гауссова (Рисунок 3.) фильтра выглядит следующим образом:
. Сравнивались два метода сглаживания изображений: на основе предложенной функции и с использованием фильтра Гаусса [4, 5]. Двумерная функция Гауссова (Рисунок 3.) фильтра выглядит следующим образом:
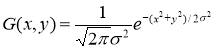 (2)
(2)
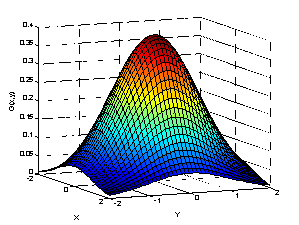
Рис. 3. График двумерной функции фильтра Гаусса
Очистка изображений от шума проводилась фильтрами из Таблицы 1. Далее в тексте они используются как фильтры — (1–6) соответственно. Для оценки качества работы фильтров была использована числовая характеристика PSNR, или пиковое отношение сигнал-шум, между двумя изображениями (оригиналом и полученным изображением). Вычисляется данная характеристика по формуле:
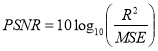 (3)
(3)
где 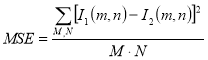 — среднеквадратическая ошибка сравнения качества восстановленного изображения;
— среднеквадратическая ошибка сравнения качества восстановленного изображения; ![]() — максимальное колебание входного сигнала изображения. Так как величина
— максимальное колебание входного сигнала изображения. Так как величина ![]() имеет логарифмическую природу, единицей ее измерения является децибел (Дб). Чем больше величина PSNR, тем лучше качество восстановленного изображения, для тождественно равных изображений
имеет логарифмическую природу, единицей ее измерения является децибел (Дб). Чем больше величина PSNR, тем лучше качество восстановленного изображения, для тождественно равных изображений ![]() . При исследовании алгоритмов сжатия и очистки от шума изображений в оттенках серого практически пригодной считается величина
. При исследовании алгоритмов сжатия и очистки от шума изображений в оттенках серого практически пригодной считается величина ![]() , изменяющаяся в пределах от 20 Дб до 50 Дб [12, 13].
, изменяющаяся в пределах от 20 Дб до 50 Дб [12, 13].
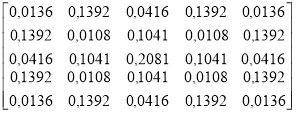
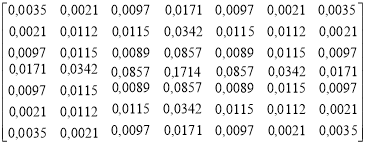
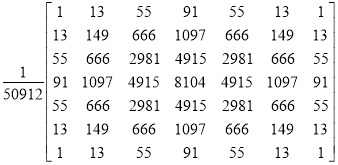
Таблица 1
Использованные сглаживающие фильтры
|
№фильтра |
Название |
Размерность |
Вид |
|
1 |
Предложенный фильтр |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
Гауссов фильтр |
|
|
|
5 |
|
|
|
|
6 |
|
|
Пример восстановления искаженного изображения с помощью фильтра показан на Рисунке 4. На рисунках 4а — 4в представлены зашумленные изображения, а на рисунках 4г — 4и восстановленные.

Рис. 4. Пример очистки изображения от шума с помощью предложенного фильтра и Гауссова фильтра размерностью ![]() . Зашумленные изображения: а) с дисперсией
. Зашумленные изображения: а) с дисперсией ![]() ; б) с дисперсией
; б) с дисперсией ![]() ; в) с дисперсией
; в) с дисперсией ![]() . Очищенные от шума предложенным фильтром изображения: г) с дисперсией
. Очищенные от шума предложенным фильтром изображения: г) с дисперсией ![]() ; д) с дисперсией
; д) с дисперсией ![]() ; е) с дисперсией
; е) с дисперсией ![]() . Очищенные от шума Гауссовым фильтром изображения: ж) с дисперсией
. Очищенные от шума Гауссовым фильтром изображения: ж) с дисперсией ![]() ; з) с дисперсией
; з) с дисперсией ![]() ; и) с дисперсией
; и) с дисперсией ![]()
Результаты эксперимента представлены в Таблице 2.
Таблица 2
Сравнение качества восстановленных изображений PSNR, Дб
|
Дисперсия |
№фильтра |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
0.01 |
24.79 |
24.39 |
23.85 |
24.59 |
24.24 |
24.25 |
|
0.05 |
22.39 |
22.22 |
21.91 |
22.31 |
22.13 |
22.13 |
|
0.25 |
12.09 |
12.10 |
12.09 |
12.10 |
12.09 |
12.09 |
Из Таблицы 2 видно, что предложенный нами фильтр не уступает фильтру Гаусса, наоборот даже дает лучший результат при очистке изображений от шума.
Заключение.
В работе исследован вопрос о применении сглаживающих фильтров для очистки от шума изображений в оттенках серого. Предложена новая функция, порождающая маску сглаживающего фильтра. Результаты моделирования показали, что предложенный фильтр дает хороший результат очистки изображений от шума, вычислительно проще и удобней в использовании.
Интересным направлением дальнейших исследований является изучение вопроса об очистке изображений от шума в конкретных областях: медицинской диагностике, биологии, обработка спутниковых снимков, археологические исследования и т. д.
Литература:
- Дороничева А. В. Методы распознавания медицинских изображений для задач компьютерной автоматизированной диагностики// Современные проблемы науки и образования [Электронный ресурс]/А. В. Дороничева, С. З. Савин. — М.: science-education.ru, 2015. – Режим доступа: http://www.science-education.ru/118–14414
- Применение радарной интерферометрии при изучении подработанных территорий/ Ж. З. Толеубекова, Д. В. Мозер, А. К. Омарова, А. С. Туякбай // ИНТЕРЭКСПО ГЕО-Сибирь. – 2012. – том 1.
- Быков А. Л. Применение материалов аэрофотосъемки с беспилотного летательного аппарата для картографического обеспечения археологических работ / А. Л. Быков, Костюк А. С., Быков В. Л. // ИНТЕРЭКСПО ГЕО-Сибирь. – 2013. – № 1, том 4.
- Jain Ramesh, Kasturi Rangachar, Brian G. Schunck. Machine vision.- Published by McGraw-Hill, Inc., 1995, 549 p.
- Shih Frank Y. Image processing and pattern recognition: fundamentals and techniques.-NY: WILEY, 2010, 537 p.
- Яне Б. Цифровая обработка изображений / Яне Б. — М: Техносфера, 2007. — 584с.
- Гонсалес Р. Цифровая обработка изображений в среде MATLAB / Р. Гонсалес, Р. Вудс, С. Эддинс — Москва: Техносфера, 2006. — 616 с.
- Bovik Al. Handbook of image and video processing. – Texas: Elsevier, 2005, 1372 p.
- Карташев В. Г. Основы теории дискретных сигналов и цифровых фильтров / В. Г. Карташев. — М.: Высш. шк., 1982.
- Прэтт У. Цифровая обработка изображений / У.Прэтт — М.: Мир, 1982. — 790 с.
- Хемминг Р. В. Цифровые фильтры / Р. В. Хемминг: Пер. с англ. / Под ред. А. М. Трахтмана. — М.: Сов. радио, 1980.
- Salomon D. Data Compression. — Springer-Verlag London, 2007, 1092 P.
- Huynh-Thu Q., Ghanbari M. Scope of validity of PSNR in image/video quality assessment // Electronics Letters, Vol. 44, № 13, 2008, pp. 800–801.
[1] Работа выполнена при финансовой поддержке гранта Президента Российской Федерации МК-5980.2016.9.