Исследование алгоритмов пост-квантовой криптографии, основанных на хэш-функциях, и последующая разработка алгоритма, в основу которого берётся ГОСТ РФ 34.11–12 «Стрибог» и дерево Меркла.
Ключевые слова: пост-квантовая криптография, хэш-функция, электронно-цифровая подпись, дерево Меркла
Алгоритмы электронно-цифровой подписи являются одним из важнейших инструментов криптографии и обеспечивают целостность электронного документа, аутентификацию и неотказуемость автора документа. Электронно-цифровая подпись в настоящее время применяется для обеспечения безопасности банковских транзакций, в государственных закупках, электронном документообороте, налоговой отчетности, в сетевых протоколах и т. д.
Те алгоритмы ЭЦП, которые используются в настоящее время, основываются на односторонней функции, а также на криптографической хэш-функции. Односторонняя функция в свою очередь основана на определенной сложной математической проблеме, для которой неизвестно эффективных алгоритмов решения. Например, алгоритм ЭЦП ECDSA использует проблему вычисления дискретного логарифма в группе точек эллиптической кривой, а другой широко известный алгоритм ЭЦП — RSA берёт в свою основу проблему факторизации больших целых чисел. Все перечисленные алгоритмы ЭЦП являются стойкими, поскольку для решения лежащих в их основе математических проблем известны лишь неэффективные, а именно, в лучше случае субэкспоненциальные алгоритмы. Следует отметить, что речь идет об алгоритмах, предназначенных для исполнения на классическом электронном компьютере. Однако еще в 1980-х годах была предложена идея использовать явления квантовой суперпозиции и квантовой запутанности для передачи и обработки данных. Вычислительное устройство, основанное на этих принципах, называется квантовым компьютером. В 1994 г. Питер Шор разработал полиномиальный алгоритм факторизации для квантового компьютера. Небольшая модификация этого алгоритма позволяет решать также задачу дискретного логарифма. Высокая эффективность алгоритма Шора означает, что криптографические алгоритмы, использующие проблемы факторизации и дискретного логарифма, потенциально являются нестойкими при наличии полноценного квантового компьютера.
Появление алгоритма Шора способствовало созданию новой области криптографии — пост-квантовой криптографии, которая изучает алгоритмы, стойкие ко взлому на квантовом компьютере. Стоит заметить, что на сегодняшний день такого компьютера ещё не существует. Однако, учитывая скорость современного технического прогресса, появление такого компьютера не стоит считать слишком отдалённым будущим, поэтому пост-квантовая криптография является актуальной областью исследований в настоящее время.
Одним из наиболее перспективных направлений пост-квантовой криптографии является криптография, основанная на хэш-функциях. Алгоритмы этого направления применяются для формирования и проверки ЭЦП и используют только криптографически стойкую хэш-функцию. В России существует ГОСТ РФ 34.11–12, другое его название — «Стрибог» [1]. На данный момент уже есть множество работ по криптоанализу данного алгоритма, но почти все они смогли привести лишь теоретически реализуемые атаки. На практике же количество вычислений для нахождения коллизий будет огромным и ресурсозатратным, поэтому алгоритм Стрибог считается безопасным алгоритмом.
Предлагаемый алгоритм подписи основан на следующих компонентах:
− Односторонняя криптографически стойкая хэш-функция «Стрибог»;
− Одноразовая подпись;
− Дерево Меркла.
Примерами одноразовых подписей являются подпись Лампорта и Винтерница [2]. Стоит учитывать, что при использовании подписи Винтерница открытый ключ будет намного короче за счет того, что одновременно подписывается ![]() бит.
бит.
Основные преимущества схемы одноразовой подписи как Лампорта, так и Винтерница заключаются в том, что они могут быть построены на любой стойкой криптографической хэш-функции. В качестве этой функции в нашем пост-квантовом алгоритме мы будем использовать хэш-функцию «Стрибог». В то же время схема имеет ряд недостатков. Во-первых, недостатком является одноразовость ключей. То есть, при подписи каждого нового сообщения приходиться генерировать новую пару, что приводит к усложнению системы. Во-вторых, схема имеет недостаток в виде большого размера подписи и пары из открытого и закрытого ключей.
В [3] Меркл представил свою схему подписи Меркла в которой один открытый ключ используется для того, чтобы подписать множество сообщений, что и решает проблему с вынужденной постоянной генерацией пары ключей для каждого нового сообщения.
Опишем принцип генерации ключа. Во-первых, стоит заметить, что схема подписи Меркла может использоваться только для подписи ограниченного числа сообщений одним открытым ключом ![]() . Обозначим возможное количество сообщений как
. Обозначим возможное количество сообщений как ![]() . Первым шагом в генерации этого единственного открытого ключа pub будет генерацией ключевых пар открытых и закрытых ключей
. Первым шагом в генерации этого единственного открытого ключа pub будет генерацией ключевых пар открытых и закрытых ключей ![]() в количестве, как и сообщений,
в количестве, как и сообщений, ![]() . Затем для каждого открытого ключа
. Затем для каждого открытого ключа ![]() , где
, где ![]() высчитывается хэш-значение
высчитывается хэш-значение ![]() . С высчитанными хэш-значениями
. С высчитанными хэш-значениями ![]() строится дерево Меркла (его также называют хэш-деревом). Обозначим узел дерева как
строится дерево Меркла (его также называют хэш-деревом). Обозначим узел дерева как ![]() , где
, где ![]() – число, означающее уровень узла дерева. Уровень узла определяется расстоянием от узла до листа. Следовательно, уровень листа дерева
– число, означающее уровень узла дерева. Уровень узла определяется расстоянием от узла до листа. Следовательно, уровень листа дерева ![]() , при этом уровень корня определяется как
, при этом уровень корня определяется как ![]() . Мы пронумеруем все узлы одного уровня слева на право так, чтобы
. Мы пронумеруем все узлы одного уровня слева на право так, чтобы![]() было самым левым узлом уровня
было самым левым узлом уровня![]() . В дереве Меркла хэш-значения – это листья бинарного дерева такие, что
. В дереве Меркла хэш-значения – это листья бинарного дерева такие, что ![]() Каждый внутренний узел дерева - это хэш-значение конкатенации двух дочерних хэшей этого узла. Так
Каждый внутренний узел дерева - это хэш-значение конкатенации двух дочерних хэшей этого узла. Так ![]() и
и ![]() . Пример дерева Меркла для высоты
. Пример дерева Меркла для высоты ![]() иллюстрировано на рисунке 1.
иллюстрировано на рисунке 1.
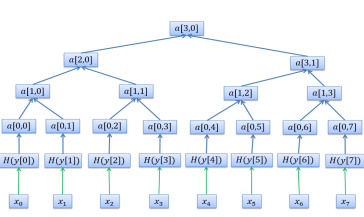
Рис. 1. Пример дерева Меркла с 8-мью листьями
Таким образом, строится дерево с ![]() листьями и узлами в количестве
листьями и узлами в количестве ![]() . Корень дерева
. Корень дерева ![]() – это и есть тот самый открытый ключ pub схемы подписи Меркла.
– это и есть тот самый открытый ключ pub схемы подписи Меркла.
Чтобы подписать сообщение ![]() при помощи подписи Меркла, это сообщение сперва подписывается односторонней ЭЦП, при этом, конечно же, вычисляется подпись
при помощи подписи Меркла, это сообщение сперва подписывается односторонней ЭЦП, при этом, конечно же, вычисляется подпись ![]() . Это делается при помощи одной ключевой пары
. Это делается при помощи одной ключевой пары ![]() которая выбирается из дерева. Лист хэш-дерева, соответствующий открытому ключу
которая выбирается из дерева. Лист хэш-дерева, соответствующий открытому ключу ![]() является хэш значением данного ключа и представляется, как
является хэш значением данного ключа и представляется, как ![]() . Путь в хэш-дереве от
. Путь в хэш-дереве от ![]() до корня назовём
до корня назовём ![]() . Путь
. Путь ![]() состоит из
состоит из ![]() узлов. Обозначим их как
узлов. Обозначим их как ![]() , где
, где ![]() это лист и
это лист и ![]() это корень дерева. Чтобы вычислить этот путь
это корень дерева. Чтобы вычислить этот путь ![]() , нам нужны все «дети» узлов
, нам нужны все «дети» узлов ![]() . Мы знаем, что
. Мы знаем, что ![]() является дочерним узлом узла
является дочерним узлом узла ![]() . Чтобы высчитать этот самый следующий узел
. Чтобы высчитать этот самый следующий узел ![]() нужно знать всех обоих «детей» этого самого узла. Следовательно, нам нужен смежный узел c узлом
нужно знать всех обоих «детей» этого самого узла. Следовательно, нам нужен смежный узел c узлом ![]() . Назовём этот узел
. Назовём этот узел ![]() , так что:
, так что:
![]() .
.
Поэтому можно сказать, что для того, чтобы высчитать все узлы, из которых состоит путь ![]() , нам понадобятся
, нам понадобятся ![]() узлов, которые можно представить, как
узлов, которые можно представить, как ![]() . Высчитаем эти узлы
. Высчитаем эти узлы ![]() и сохраним их в памяти. Эти узлы, плюс односторонняя подпись
и сохраним их в памяти. Эти узлы, плюс односторонняя подпись ![]() сообщения
сообщения ![]() есть искомая подпись Меркла, которая обозначается, как
есть искомая подпись Меркла, которая обозначается, как
Пример аутентификационного пути ![]() представлен на рисунке 2.
представлен на рисунке 2.
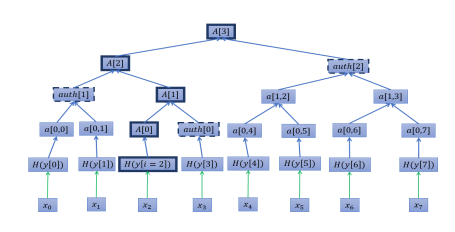
Рис. 2. Дерево Меркла с путём ![]() и путём аутентификации для
и путём аутентификации для ![]()
Теперь опишем подтверждение подписи. Получателю известен открытый ключ ![]() , сообщение
, сообщение ![]() и подпись
и подпись ![]() . Получатель подтверждает одноразовую подпись
. Получатель подтверждает одноразовую подпись ![]() сообщения
сообщения ![]() . Если подпись
. Если подпись ![]() верна для сообщения
верна для сообщения ![]() , получатель вычисляет
, получатель вычисляет ![]() путём хэширования открытого ключа одноразовой подписи. Для
путём хэширования открытого ключа одноразовой подписи. Для ![]() , узлы
, узлы ![]() пути
пути ![]() вычисляются по формуле:
вычисляются по формуле:
![]() .
.
Если ![]() получится равным открытому ключу подписи Меркла, то подпись верна.
получится равным открытому ключу подписи Меркла, то подпись верна.
Основным недостатком алгоритмов на деревьях Меркла является проблема хранения большого количества закрытых ключей и их последующая передача. Чтобы решить данную проблему, можно на основе одного секретного ключа небольшого размера создать криптографически стойкий генератор псевдослучайных чисел (КСГПСЧ), который будет заполнять все массивы закрытых ключей. Тогда этот один ключ можно будет передавать быстрее и сам он не будет таким требовательным к памяти.
Данный генератор даст нам возможность передавать хранить в памяти небольшой закрытый ключ вместо внушительного количества закрытых ключей. Будем использовать в качестве односторонней ЭЦП алгоритм Винтерница. Введём обозначения:
![]() – счётчик для количества ключей в дереве Меркла;
– счётчик для количества ключей в дереве Меркла;
![]() – счётчик для алгоритма Винтерница.
– счётчик для алгоритма Винтерница.
Процесс генерации секретных и открытых ключей выглядит следующим образом:
![]()
![]()
На место ![]() в первой формуле далее ставим значение предыдущего столбца в двумерном массиве ключа. Введём дополнительный параметр:
в первой формуле далее ставим значение предыдущего столбца в двумерном массиве ключа. Введём дополнительный параметр: ![]() . Начальное значение будет
. Начальное значение будет ![]() , то есть заполнение каждого ключа будет идти по правилу:
, то есть заполнение каждого ключа будет идти по правилу:
![]()
Далее:
![]()
![]()
Этот вариант алгоритма можно считать более приемлемым, поскольку, введя счётчики мы повышаем вероятность случайного выпадения бита, а также уменьшаем вероятность того, что в открытых ключах будут повторы битов из закрытых ключей.
Литература:
- ГОСТ РФ 34.11–2012. Информационная технология. Криптографическая защита информации. Функция хеширования. — Введ. 2012–07–08. — М.: Стандартинформ, 2012. — 38 с.
- Bernstein D. J. Post-Quantum Cryptography / D. J. Dernstein, J. Buchman, E. Duchman — Ch.: Springer, 2008. — 248 p.
- Ralph Merkle. Secrecy, authentication and public key systems/ A certified digital signature. Ph.D. dissertation, Dept. of Electrical Engineering, Stanford University. – 1979 – 193 с.







