Исследование возможности построения гибридной схемы шифрования для алгоритмов машинного обучения на основе алгоритмов криптографического преобразования ГОСТ РФ 28147–89 и алгоритмом Фана и Веркаутерена.
Ключевые слова: гомоморфное шифрование, ГОСТ 28147–89, машинное обучение
Обеспечение конфиденциальности является одной из основных задач информационной безопасности. С развитием современных технологий увеличился объем сбора, хранения и обработки информации, рост объемов требует внедрения новых методов и алгоритмов анализа данных.
Для решения этой задачи часто применяется метод машинного обучения — актуальной и интенсивно развивающейся области знаний, направленной на обработку больших объемов информации. Но активное внедрение приложений интеллектуального анализа данных и алгоритмов машинного обучения позволяют злоумышленникам использовать интеллектуальный анализ данных для получения частной информации. Поэтому встает вопрос о противодействии угрозам путем шифрования конфиденциальных данных и создании таких алгоритмов, которые могли бы обнаружить те же сведения из модифицированных данных так же полностью и правильно, как из исходных данных.
Общая схема работы алгоритма обучения по прецедентам над конфиденциальными данными состоит из двух фаз: обучения и применения, на которой алгоритм работает над вектором признаков, не встречающихся в обучающей выборке. При этом оба этапа проходят в режиме секретности и никакие сведения о работе схемы не раскрываются. Исходные данные и результат работы могут быть доступны только клиенту, отправляющему запрос, а модель получения результата — обрабатывающему серверу.
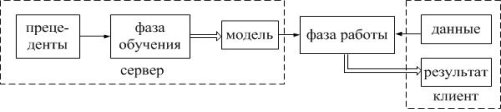
Рис. 1. Общая схема машинного обучения над зашифрованными данными
Общая схема машинного обучения над зашифрованными данными представлена на рисунке 1. Пунктирными линиями выделены зоны конфиденциальности и данные которые доступны в этой области одному из участников. Одиночные стрелки указывают входные данные алгоритма, а двойные стрелки указывают результаты.
Наиболее перспективным методом шифрования в схемах машинного обучения является гомоморфное шифрование. Схема шифрования называется гомоморфной для некоторых операций ![]() ∈ FM (таких как сложение и умножение), действующих в пространстве сообщений, если существуют соответствующие операции ⋄ ∈ FC, действующие в шифрованном текстовом пространстве, удовлетворяющие свойству:
∈ FM (таких как сложение и умножение), действующих в пространстве сообщений, если существуют соответствующие операции ⋄ ∈ FC, действующие в шифрованном текстовом пространстве, удовлетворяющие свойству:
Заметим, что это не групповой гомоморфизм в математическом смысле, так как из-за семантической безопасности свойство гомоморфности не коммутируется. То есть, поскольку одно и то же сообщение с высокой вероятностью шифрует различные шифрованные тексты, то:
![]()
Более того,![]() .
.
Схема гомоморфного шифрования, использующая операции сложения и умножения, получила название полного гомоморфного шифрования, и для нее справедливо следующее условие:
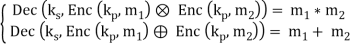
Но открывшиеся теоретические возможности сдерживаются практическими ограничениями — нельзя говорить о внедрении гомоморфного метода в уже существующие алгоритмы без их существенного изменения: возникают трудности как с логикой построения алгоритма, так и с вычислительными возможностями [1, c 72].
Ограничение на работу с целыми числами, количество возможных операций сложения и умножения из-за возрастающего криптографического шума, означает, что на практике гомоморфное шифрование позволяет работать только над зашифрованными данными, представленными в виде полиномов. Но даже в этом случае работа таких алгоритмов будет относительно медленной и ресурсозатратной, а размеры шифротекстов занимают большое пространство в памяти [2, c 3].
Так же серьезным ограничением является невозможность использовать какой-либо условный код: операции сравнения, а так же тесты равенства и неравенства, не могут выполняться над зашифрованными данными.
Одним из предлагаемых решений проблемы увеличения размера шифротекста является предварительное шифрование сообщений каким-либо другим стандартом а при обращении к сообщению перекодирование его в гомоморфную схему.
Нами была рассмотрена возможность построения гибридной схемы шифрования, основанной на стандарте ГОСТ 28147–89. Идея состоит в упрощении этапа шифрования и отправки шифротекста клиентом за счет использования более быстродейственного стандарта ГОСТ 28147–89. Полученное сообщение клиент отправляет сервер, где уже вычислительными силами исполнителя производятся вычисления, основанные на методе гомоморфизма. Такое изменение позволит уменьшить объем сообщения, отправляемого клиентом, и вычислительные затраты на криптопреобразование.
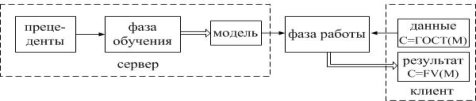
Рис. 2. Общая схема машинного обучения над зашифрованными данными
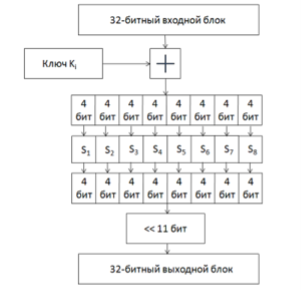
Рис. 3. Структура работы ГОСТ 28147–89
Рассмотрим режим простой замены для ГОСТ 28147–89. 64-битный блок открытого текста разбивается на две Части А и В. Для генерации подключей исходный 256-битный ключ разбивается на восемь 32-битных блоков: K1…K8. Ключи K9…K24 являются циклическим повторением ключей K1…K8. Ключи K25…K32 являются ключами K8…K1.
![]() , где
, где ![]() )
)
![]()
После выполнения всех 32 раундов алгоритма, блоки A33 и B33 склеиваются. Результат разбивается на восемь 4-битовых последовательностей, каждая из которых поступает на вход своего узла таблицы замен (в порядке возрастания старшинства битов), называемого ниже S-блоком. Общее количество S-блоков стандарта — восемь, то есть столько же, сколько и последовательностей. Каждый S-блок представляет собой перестановку чисел от 0 до 15 (конкретный вид S-блоков в стандарте не определен).
В качестве алгоритма, обрабатывающего сообщение на сервере была выбрана схема Fan and Vercauteren. Для обеспечения работы гибридной схемы шифрования необходимо представить схему шифрования ГОСТ 28147–89 как набор операций сложения и умножения, доступных для алгоритма [2]. Так, для выполнения сложения по модулю ![]() необходимо представить числа в виде суммы
необходимо представить числа в виде суммы 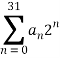 , а на основе выбранной таблицы замен построить таблицы истинности и вывести СКНФ с избавлением от отрицания для выполнения замен значений без использования операторов сравнения.
, а на основе выбранной таблицы замен построить таблицы истинности и вывести СКНФ с избавлением от отрицания для выполнения замен значений без использования операторов сравнения.
Теперь подробнее рассмотрим схему [2]. Введем систему обозначений для ее подробного рассмотрения.
Пусть ![]() — множество целых чисел, такое, что
— множество целых чисел, такое, что ![]() , а
, а ![]() — целое число в
— целое число в ![]() , равное
, равное ![]() .
. ![]() и
и ![]() — многочлены, коэффициенты которых принадлежат
— многочлены, коэффициенты которых принадлежат ![]() и
и ![]() соответственно.
соответственно.
Алгоритм работает с кольцами полиномов
Полиномы ![]() , не записанные в функциональной форме
, не записанные в функциональной форме ![]() , будут выделены подчеркиванием. Полиномиальное умножение внутри кольца
, будут выделены подчеркиванием. Полиномиальное умножение внутри кольца![]() так же будет выделено подчеркиванием полиномов, участвующих в операции.
так же будет выделено подчеркиванием полиномов, участвующих в операции. ![]() указывает на то, что центрированное сокращение применяется к каждому коэффициенту
указывает на то, что центрированное сокращение применяется к каждому коэффициенту ![]() по отдельности, так что
по отдельности, так что ![]() . Если
. Если ![]() получена при помощи равномерного распределения вероятностей на множестве
получена при помощи равномерного распределения вероятностей на множестве ![]() , это обозначается как
, это обозначается как ![]() . Если
. Если ![]() получено при помощи Гауссовского распределения на множестве
получено при помощи Гауссовского распределения на множестве ![]() — это обозначается
— это обозначается ![]() .
.
Пространством сообщений этой схемы является полиномное кольцо ![]() . Шифрованное текстовое пространство является декартовым произведением двух полиномиальных колец
. Шифрованное текстовое пространство является декартовым произведением двух полиномиальных колец ![]() , где
, где ![]() .
.
Прежде чем приступить к шифрованию сообщений, необходимо определить параметры схемы. ![]() определяет степень полиномиальных колец
определяет степень полиномиальных колец ![]() и
и ![]() .
. ![]() и
и ![]() , определяют множества коэффициентов полиномиальных колец
, определяют множества коэффициентов полиномиальных колец ![]() и
и ![]() ,
, ![]() определяет величину случайности, необходимой для обеспечения семантической безопасности [2, c 4].
определяет величину случайности, необходимой для обеспечения семантической безопасности [2, c 4].
Генерация ключа. Секретный ключ![]() — это переменная, выбранная из
— это переменная, выбранная из ![]() при помощи равномерного распределения. Открытый ключ,
при помощи равномерного распределения. Открытый ключ, ![]() , представляет собой вектор, содержащий два многочлена:
, представляет собой вектор, содержащий два многочлена:
![]()
Где ![]() и
и ![]() .
.
Шифрование, ![]() целочисленное сообщение m представляется как
целочисленное сообщение m представляется как ![]() , а затем построить
, а затем построить 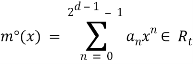 , где
, где ![]() . Шифротекст представляет собой вектор, содержащий два полинома:
. Шифротекст представляет собой вектор, содержащий два полинома:
![]()
Где ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
Дешифрование, ![]() : Расшифровка шифрованного текста c производится путем оценки:
: Расшифровка шифрованного текста c производится путем оценки:
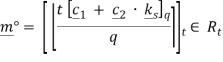 ,
, Рассмотрим выполнение операций сложения и умножения над пространством сообщений в алгоритме [2, c 5].
Сложение в пространстве шифрованных сообщений выполняется в виде сложения векторов и полиномов с модульной редукцией:
![]()
Умножение в пространстве сообщений приводит к существенному увеличению длины шифротекста и выполняется по следующей формуле:
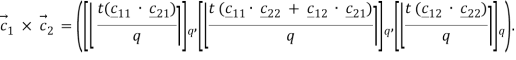
При этом можно выполнить дешифрование одного из сообщений, входящих в произведение, изменив функцию дешифрования:
![]()
Литература:
- Yi X., Paulet R., Bertino E. Homomorphic Encryption and Applications. — New York City: Springer International Publishing, 2014. — 136 p.
- Encrypted statistical machine learning // https://arxiv.org/. URL: https://arxiv.org/pdf/1508.06574v1.pdf (дата обращения: 8.06.2017).







