Металлообрабатывающий станок предназначен для предоставления обрабатывающей заготовке необходимой формы с заданной точностью путем снятия стружки. Относительные движения заготовки и режущего инструмента, в результате которых проходит процесс резки, называются основными. Основные движения разделяются на главное, при котором инструмент режет металл, и движение подачи, вызывает перемещение инструмента или обрабатываемой заготовки для снятия нового слоя металла [1].
Современный электропривод металлорежущих станков (МС) является высокоавтоматизированным устройством, что обеспечивает регулирование в широких пределах и поддержание высокой точности заданного параметра: тока, скорости, угла. В свою очередь, каждый из перечисленных параметров электропривода определяет технологические характеристики механизма или машины в целом. Процесс резки металла на МС определяет и режимы работы привода главного движения и привода подачи. Практически в любых типах МС (токарные, фрезерные, шлифовальные, строгальные и др.) приводы главного движения работают в двух режимах: регулирования скорости до номинальной и при моменте, зависящем от нагрузки (материал обрабатываемой детали, скорость подачи, глубина и ширина обработки, тип инструмента и т. п., и регулирования скорости выше номинальной при ослаблении потока и поддержании мощности [2].
Главный привод многих станков выполнен на базе асинхронных электродвигателей (АД) с короткозамкнутым ротором (КР) в связи с тем, что они наиболее дешевые и надежные в эксплуатации и удобно стыкуются с коробкой скоростей. Перспективным является использование для приводов главного движения АД с короткозамкнутым ротором с векторным управлением от тиристорных или транзисторных преобразователей.
В соответствии с теоретической структурой системы векторного управления (СВУ) АД, представленной на рис. 1 [4], в среде MATLAB была составлена модель такой системы. При этом ставились следующие задачи:
− проверка правильности синтеза параметров системы и коэффициентов регуляторов;
− проверка правильности аналитического вывода уравнений переходной механической характеристики.
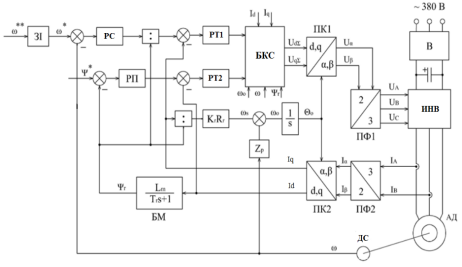
Рис. 1. Функциональная схема системы регулирования скорости электропривода при векторном управлении АД
С целью проверки работоспособности системы была построена математическая модель, на основе которой проводился анализ режимов работы. Моделирование системы проводилось для управления электроприводом главного движения станка в 1-й зоне с задачей регулирования скорости согласно технологическому процессу обработки детали при фрезеровании [3].
Исследование качества управления АД c КР осуществлено путем моделирования на ЭВМ с помощью программы «SIMULINK» программного пакета «MATLAB» [6]. Переходные процессы будем моделировать с помощью схемы с двухфазной (динамической) модели АД в координатах статора а-b [5].
Модель составлена из отдельных блоков. Каждый блок реализует определенный элемент структурной схемы. Модель содержит и другие компоненты, предназначенные для обеспечения работоспособности и визуализации результатов моделирования:
− Блок reg_velocity — ПИ регулятор скорости;
− Блок reg_flux — ПИ регулятор потокосцепления;
− Блок reg_id — ПИ регулятор тока Id;
− Блок reg_iq — ПИ регулятор тока Iq;
− Блок compensator — блок компенсации внутренних (перекрестных и прямых) связей АД;
− Блок transvec1 — модель обратной преобразования напряжения из системы координат (dq) в (ab);
− Блок transvec2 — модель прямого преобразования напряжения из системы координат (ab) в (dq);
− Блок MA_ (a, b) — модель асинхронного двигателя в стационарной системе координат;
− Блок Assignment — задатчик интенсивности, обеспечивает плавное нарастание скорости при пуске и торможении.
Моделирование проводилось для режима резания при фрезеровании [3]. Скорость вращения шпинделя 30.6 рад / с, статический момент на шпинделе 172.2 Н∙м. Учитывая, что двигатель связан со шпинделем через редуктор с коэффициентом редукции i = 2 скорость и момент на валу двигателя будут равны:
В интервале времени t от 0 до 1 с выполнялось возбуждение асинхронного двигателя. Ротор находится в состоянии покоя, то есть ω=0.
При t = 1c было подано линейно нарастающее задания скорости двигателя. Двигатель разгоняется до скорости, равной 154,026 рад/с за 0.5 с. При этом на кривой переходного процесса момента виден скачок пускового момента (рисунок 3), который поддерживается на постоянном уровне в течение 0.5с пока двигатель не выйдет на устойчивую скорость.
При t = 1…3 с продолжается устойчивый режим работы двигателя. Наброски нагрузки Mc = 81.1 Н∙м происходит в момент времени t = 3 с, нагрузка снимается в момент времени t = 3.5 с.
При t = 4.5 c плавно уменьшается задания скорости двигателя до 0. Торможение происходит за 0.5 с.
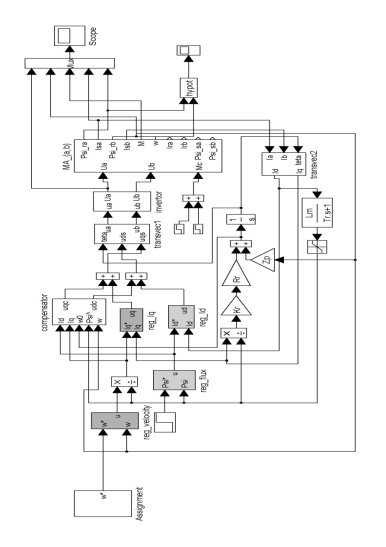
Рис. 2. Структурная схема системы управления электропривода в системе MATLAB «Simulink»
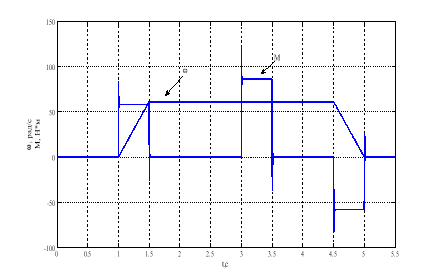
Рис. 3. Переходные процессы скорости и момента двигателя
Переходные процессы напряжений статора, токов статора и потокосцеплений ротора представлены на рисунке 4.
Анализируя полученные результаты (см. рисунок 3), полученные при моделировании, делаем следующие выводы:
1) Векторная система управления позволяет почти полностью исключить опасные броски тока и момента;
2) Перед пуском необходима пауза для возбуждения машины;
3) Система позволяет управлять моментом двигателя.
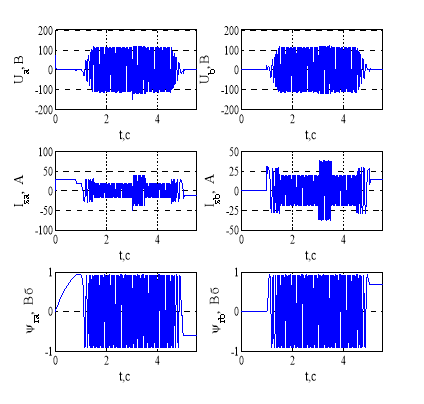
Рис. 4. Переходные процессы напряжений статора, токов статора и потокосцеплений ротора
Показатели качества при отработке возмущения:
-
1.Статическая погрешность
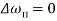рад/с.
-
Макс. динамическое падение скорости
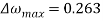рад / с.
- Перерегулирование σ = 0.4297%.
Настройки регуляторов в системе обеспечивают отсутствие статической погрешности, под действием статического момента обеспечивается ПИ- регулятором скорости.
Выводы: было проведено моделирование режима резания фрезерования. Раскрыты субсистемы блоков, из которых состоит модель. Разгон двигателя происходил плавно, перерегулирование скорости при разгоне σ = 0.8%.
Литература:
1. Справочник «Электромеханические системы автоматизации в металлообработке и машиностроении» / В. И. Теряев, С. П. Колесниченко. 2003. — 60 с.
2. Справочник по обработке металлов резанием / Ф. Н. Абрамов, В. В. Коваленко, В. Е. Любимов и др. – К.: Техника, 1983. – 239 с.
3. Соколов Н. Г., Елисеев И. А. Расчеты по автоматизированному приводу металлорежущих станков. М.: Высш. шк., 1970. — 296 с.
4. Соколовский Г. Г. Электроприводы переменного тока с частотным регулированием. – М.: ACADEMA, 2006. – 265 с.
5. Системы управления электроприводов / Под. ред. Терехов В. М. — М.: Академия, 2005. — 298 с.
6. Островерхов М. Я., Пижов В. М. Моделирование электромеханических систем в Simulink: Пособие для студентов высших технических заведений. — К.: ВД «Стилос», 2008. — 528 с.
