Некоторые способы активизации мыслительной деятельности учащихся на уроках математики

В этой статье излагаются некоторые способы активизации мыслительной деятельности учащихся на уроках математики, и даны рекомендации их применения на уроках с целью развития творческой самостоятельности учащихся.

Ключевые слова: математика, обучение, способ, активизация, мыслительная деятельность, учебник, нетрадиционные уроки, творческие задания, дидактические игры, решения задач, мотивация, интерес.

Развитие мыслительной деятельности на уроках заставляет педагогов задуматься над тем, как поддержать интерес ученика к изучаемому материалу и его мыслительную активность на протяжении всего урока. Поэтому в настоящее время интенсивно ведутся поиски новых инновационных методов обучения и таких методических способов, которые активизируют мышления учащихся, способствуют развитию активности, самостоятельности, личной инициативы и творческих способностей учащихся.

Основные этапы исследования на уроке: мотивация исследовательской деятельности; формулировка проблемы; сбор, систематизация и анализ фактического материала; выдвижение гипотез; проверка гипотез; доказательство или опровержение гипотез. Например, при изучении темы «Взаимное расположение графиков линейных функций» класс делится на группы, и учащиеся первой группы занимаются самоконтролем.

Вторая группа работает по карточкам.

1. Найдите точку на графике функции у=1,5х+3,25, абсцисса и ордината которой — противоположные числа.
2. Выразите формулой линейную функцию, график которой проходит через начало координат и точку Р (2;- 4,5).
3. Найдите точку пересечения прямой 3х-2у-16=0 с графиком этой функции.

Класс делится на группы. Каждая группа получает одно задание, в котором предлагается в одной декартовой системе координат построить три различных графика линейных функций и выяснить закономерность их расположения в зависимости от их коэффициентов, например, следующих трех функций: у=3х; у=3х-1; у=3х+2 и т. д.

Организуется обсуждение, составляется таблица предложенных гипотез, если даны функции у=k₁x+b₁ y=k₂x+b₂. Какие могут быть варианты относительно коэффициентов функций? Таких вариантов четыре:

1) k₁ =k₂, b₁ = b₂;

3) k₁ ≠k₂;

4) k₁ ≠k₂, b₁ = b₂.

Учащимся предлагается исследовать каждый из этих случаев и высказать вывод о расположении графиков линейных функций. После закрепления можно давать задания такого рода: исследовать графики функций в зависимости от значений параметра: а) у=ах+1, у=2ах-5. При этом необходимо добиться понимания того, что при равных угловых коэффициентах графики параллельны, при различных же графики пересекаются, при равных свободных членах и различных угловых коэффициентах графики пересекаются в точке оси ординат.

При изложении темы неравенства треугольника можно провести обсуждение следующих творческих заданий:

1. В каких случаях можно построить треугольник, если даны длины его сторон:

а. 5, 6, 8 (построить можно);

б. 7, 14, 7 (получается отрезок);

в. 5, 16, 7 (нельзя построить).

2. Обоснуйте, почему получаются такие результаты?
3. Проверить гипотезу: если сторона, построенная первой, меньше суммы двух других сторон, то треугольник строится.
4. Существует ли в первом случае какая-то закономерность между длинами сторон треугольника? (Проверяется гипотеза 5 см < 6 см + 8 см, значит, AB < BC + АС, 6 см < 5 см + 8 см, значит, ВС < АВ + АС, 8 см < 5 см + 6 см, значит, АС < АВ + ВС).
5. Какой вывод можно сделать?
6. Как это свойство можно сформулировать? (Каждая сторона треугольника меньше суммы двух других сторон.)
7. Почему нельзя построить треугольник в третьем случае? (В третьем случае треугольник построить нельзя, так как длина большей стороны больше суммы длин меньших сторон.)

В ходе обсуждения проблемного вопроса по теме «Теорема Виета» проводится дифференцированная работа:

1. Исследовать уравнения: х² + 5х + 6 = 0 (корни -2 и -3); х² — х — 2 = 0 (корни -1 и 2); х^2–2х — 15 = 0 (корни -2 и 5); х² +3х — 10 = 0 (корни -5 и 2); х² + х — 42 = 0 (корни -7 и 6).
2. Составить таблицу результатов, найти закономерность и сделать вывод.

При обсуждении результатов ставятся такие вопросы:

1. Есть ли связь между корнями решенных уравнений и его коэффициентами?
2. Как это можно сформулировать?
3. Как это можно доказать?
4. Верна ли следующая гипотеза: если даны корни приведенного квадратного уравнения, то их сумма равна второму коэффициенту с противоположным знаком.
5. Какая теорема называется обратной данной теореме?
6. Составьте теорему, обратной к теореме: если сумма двух чисел равна второму коэффициенту с противоположным знаком, произведение их равно свободному члену, то эти числа являются корнями приведенного квадратного уравнения.
7. Как с использованием обратной теоремы по заданным корням можно составлять квадратные уравнение?
8. Какая теорема ‑ прямая или обратная, позволяет определять знаки корней квадратного уравнения?
9. Как можно найти корни приведенного квадратного уравнения методом подбора?

При изучении теоремы Пифагора учащимся можно предложить на основе данных рисунков прямоугольных треугольников с данными сторонами заполнить таблицу, в которую вносятся квадраты сторон, суммы квадратов меньших сторон и сравнения с квадратом большой стороны (гипотенузы). В этой таблице записываются квадраты длин катетов и гипотенузы для каждого из данных треугольников: три треугольника и 3 строки таблицы.

1. Определите, как связаны катеты и гипотенуза в каждом из треугольников (как связаны квадраты катетов с квадратом гипотенузы). (Квадрат гипотенузы равен сумме квадратов катетов).
2. Как называется эта теорема?
3. Знаете ли вы способы доказателстьва этой теоремы?
4. Что знаете о Пифагоре?

Демонстрируется презентация о теореме. В нем подчеркивается, что это самая известная теорема геометрии, с этой теоремой знакомы подавляющее большинство людей, а доказать ее могут лишь очень немногие.

Дан прямоугольныйтреугольник, а, в ‑ катеты, с ‑ гипотенуза. Доказать с² =а²+в²

Доказательство.

1. Рассмотрим прямоугольный треугольник с катетами, равными а и b, и гипотенузой, равной с.
2. Построим, например, прямоугольный треугольник с катетами: a= 3 см, b = 2см.
3. Достроим треугольник до квадрата со стороной .
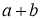4. Площадь этого квадрата равна .
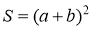5. Этот квадрат составлен из четырех равных прямоугольных треугольников с площадями 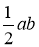и квадрата со стороной ,
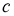6. Значит.
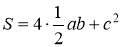7. Вывод .

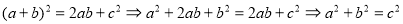Сравнивают свой вывод с теоремой, предложенной в учебнике и известной как теорема Пифагора.

Большую пользу для развития мышления имеют задачи занимательного характера. Здесь необходимо подчеркнуть задачи исторического содержания. Такие, как связанные с именами ученых, писателей и других знаменитостей, например, задача Фибоначчи о кроликах, принцип Дирихле, задача Ньютона о коровах, задача Толстого об артели косцов, задача о фальшивых монетах, задачи из китайского трактата «Математика в девяти книгах», задачи из книги «Алиса в стране Зазеркалье». А также задачи тематического содержания: задачи на переливания, задачи на смеси; задачи, связанные с календарем; задача о Кенигсбергских мостах, задачи на четность, задачи на применение кругов Эйлера, задачи с логическим и комбинаторным содержанием, задачи из знаменитых сборников задач, например, из арифметики Магницкого, задачи из книг по занимательной математике, авторами которых являются Я. И. Перельман, Б. А. Кордемский, М. Гарднер и т. д.

Кроме того, для активизации мышления имеет значение решение задач и доказательство теорем различными способами. Например, учащимся можно предложить такие задания: найти различные способы решения квадратного уравнения; найти различные способы доказательства теоремы Пифагора, теоремы синусов и т. д. Можно применять такой метод, когда после решения любого уравнения или неравенства предложить найти способ решения и сравнить с предыдущим способом, определив, какой из них оптимальный, т. е. такой, который быстро приведет к решению задачи и с математической точки зрения изящен.

Резюмируя, можно сказать, что активизация мышления связана не только отбором содержания изучаемого материала, но и использованием методов обучения, которые позволяет эффективно управлять мыслительными действиями в процессе решения поставленных учебных проблем и корректировкой их при формировании у учащихся прочных и глубоких знаний и умений по математике.

Литература

1. Семушин, А. Д.; Егоров, Е. Е.; Кретинин, О. С. Активизация мыслительной деятельности учащихся в процессе обучения математике. – М.: Просвещение, 1981.
2. Абдуллаев, А. Н.; Инатов, А. И.; Останов, К. О применении информационных технологий для формирования информационно-коммуникативной компетентности учащихся на уроках математики // Молодой ученый. Международный научный журнал, № 14(148), 2017, Ч. 7, с. 583–585.