Ключевые слова: гидравлическая система, гибридная система, компьютерное моделирование, обратная связь
Многие природные и техногенные явления и процессы подчиняются законам гидродинамики. Среди них — движения воздушных и океанических масс; движения плазмы и грунтовых вод в недрах Земли, циркуляция крови в кровеносных сосудах людей и животных и т. д. Увидеть реальную картину протекания жидкости в большинстве случаев дорого или невозможно. Понять природу процессов и существующие закономерности позволяет компьютерное моделирование [1]. Компьютерная модель позволяет провести множество экспериментов с различными начальными условиями и/или параметрами модели.
Целью работы является разработка математического и программного обеспечения для построения и численного анализа простых гидравлических систем переменной структуры. Переменная структура обусловлена наличием в системе медленных (непрерывных) и быстрых (дискретных) процессов. Системы с такими особенностями принято называть гибридными системами (ГС) [2]. В литературе также используются термины «непрерывно-дискретные системы», «системы с переменной структурой», «событийно-управляемые». Непрерывные режимы, как правило, описываются системами алгебро-дифференциальных уравнений, а дискретные события — логическими предикатами. При обращении предиката в true происходит смена непрерывного режима.
Поведение ГС можно представить последовательностью сменяющих друг друга сложных длительных непрерывных и сложных мгновенных дискретных переходов, образующих общую системную траекторию (рисунок 1). Саму ГС можно представить в виде графа смены непрерывных поведений (карта поведения, statechart), в котором каждая вершина определяет поведение в текущий момент времени, а каждая дуга — условия смены поведений и выполняемые при этом действия [3].
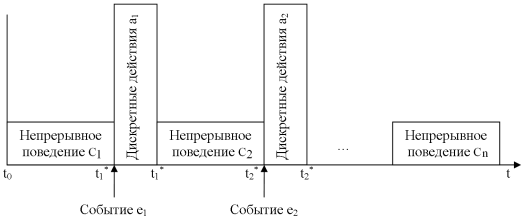
Рис. 1. Геометрическая интерпретация глобального поведения ГС
Проявление объектом исследования и непрерывных и дискретных аспектов поведения может быть обусловлено следующими факторами:
– совместным функционированием непрерывных и дискретных объектов;
– мгновенными изменениями в непрерывном объекте, обусловленными его физическими свойствами;
– изменением состава системы в процессе функционирования.
Построение гибридной модели системы целесообразно, когда в реальной системе присутствуют и дискретные и непрерывные процессы, и все они являются существенными для анализа системы.
Язык описания модели. Для описания модели гидравлической системы разработан специализированный графический язык. Реализацией является графический редактор, реализованный в виде web-приложения (рисунок 2).
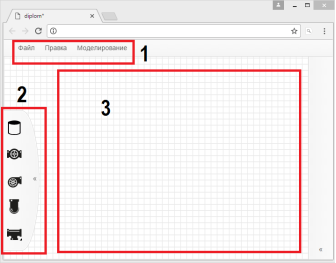
Рис. 2. Редактор гидравлических систем: 1 — главное меню; 2 — графические примитивы; 3 — область построения модели
Композиция модели возможна из следующих примитивов (рисунок 2, область 2, сверху вниз):
– бак (резервуар, способный накапливать жидкость в ограниченных объемах). Атрибуты элемента: высота, площадь основания, начальный уровень жидкости, список входных/выходных коннекторов;
– вентиль (элемент управления потоком жидкости; позволяет выполнять мгновенное перекрытие/открытие трубы). Атрибутом элемента является состояние (закрыт/открыт) (рисунок 3);
– насос (элемент для генерации входного потока/потоков жидкости). Атрибуты элемента: интенсивность потока;
– слив (элемент для утилизации жидкости из системы);
– разветвление (элемент, позволяющий выполнить разделение потока). Возможно деление потока на два (тройник) или три (крест) эквивалентных потока.

Рис. 3. Состояние вентиля: а) — открыт; б) — закрыт
Каждый примитив снабжен специальными коннекторами для формирования связи. Количество коннекторов бака можно регулировать с помощью команд контекстного меню (рисунок 4).
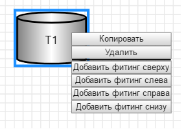
Рис. 4. Команды добавления коннекторов бака
Возможно управление параметрами объекта модели (рисунок 5).
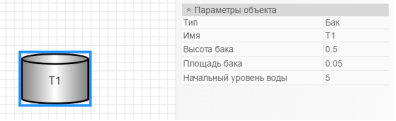
Рис. 5. Управление параметрами объекта
Соединение примитивов модели происходит путем совмещения их коннекторов (рисунок 6). Наличие незадействованного коннектора в модели является ошибкой.
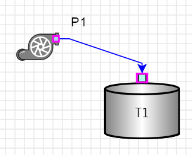
Рис. 6. Композиция модели
Разработанная система реализует следующую функциональность:
– построение модели из набора примитивов;
– проверка корректности модели;
– построение математической модели (получение дифференциальных уравнений динамики жидкости в баках для каждого непрерывного режима);
– проведение компьютерного эксперимента (моделирование динамических процессов в системе с визуализацией результатов).
Моделирование системы двух резервуаров. Для демонстрации работы разработанной системы рассмотрим систему двух резервуаров [4]. Система состоит из двух баков T1 и T2. Баки соединены двумя трубами. Насос P поставляет жидкий поток Qp в бак T1. Четыре переключаемых клапана V1, V2, V3 и V4 позволяют управлять потоками Q1, Q2, Q3 и Q4. Величины потоков определяются в соответствии с законом Торричелли: ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Где A1, A2, A3, A4 — площадь сечения трубок.
. Где A1, A2, A3, A4 — площадь сечения трубок.
Насос P управляется таким образом, чтобы удерживать уровень жидкости h2 между двумя заданными значениями. Поток Qp может принимать два значения: Qp = 0 и Qp = Q0.
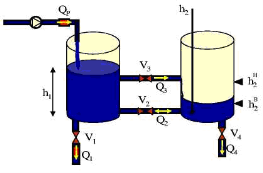
Рис. 7. Система двух баков
Клапаны V1, V2, V3 и V4 управляются вручную. Рассмотрим случай, когда V1, V2, V3 открыты всегда, а V4 меняется в соответствии с событиями e1 и e2, которые наступают в моменты времени t=240 с и t=380 с соответственно. По e1 клапан V4 открывается, по e2 — закрывается.
При запуске процесса моделирования генерируется математическая модель (рисунок 8) и выполняется численный расчет модели с анимацией результата в реальном времени (рисунок 9).

Рис. 8. Математическая модель
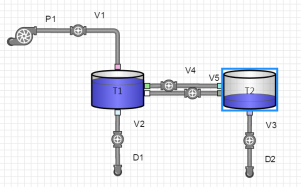
Рис. 9. Численный расчет с анимацией результатов
Также доступен режим интерпретации результатов моделирования в виде временных диаграмм (рисунок 10).
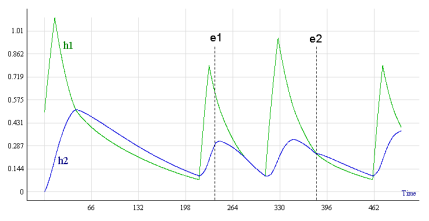
Рис. 10. Временные диаграммы уровней жидкости в баках
Заключение. Разработана система моделирования простых гидравлических систем. Для описания модели разработан специализированный графический язык. Системы подобного рода могут быть полезны при обучении или для практического моделирования. Преимуществом является ориентация на конкретную предметную область, что существенно облегчает процесс построения модели предметным специалистом.
Литература:
- Бенькович Е. С., Колесов Ю. Б., Сениченков Ю. Б. Практическое моделирование динамических систем. — СПб.: БХВ-Петербург, 2002. — 464 с.
- Шорников Ю. В. Инструментально-ориентированный анализ гибридных систем различной природы / Ю. В. Шорников, Д. Н. Достовалов, И. Н. Томилов // Научный вестник Новосибирского государственного технического университета. — 2013. — № 3. — С. 102–110.
- Колесов Ю. Б. Моделирование систем. Объектно-ориентированный подход: Учебное пособие / Ю. Б. Колесов, Ю. Б. Сениченков. — СПб.: БХВ–Петербург, 2006. — 192 с.
- Kowalewsky S., Stursberg O., and others. A Case Study in Toll-Adier Analysis of Discretaly Controlled Continuous System: The Two Tanks Problem. — Presented at the 15 International Workshop on Hybrid System, 1997.







