В статье рассматриваются основы моделирования прогноза показателей. Рассмотрены временные ряды, как основа прогноза различных явлений, так как действующие факторы влияли в прошлом, продолжают действовать в настоящем, и ожидается, что они будут действовать схожим образом и в недалеком будущем.
Ключевые слова: прогнозирование, моделирование, временные ряды, доверительный интервал, стохастическая зависимость
Временной ряд представляет собой последовательность значений, которые характеризуют изменение некоторого показателя во времени.
Основной целью анализа временных рядов являются оценка и вычленение влияющих факторов по имеющимся данным о системе для прогнозирования ее поведения в будущем и выработки рациональных управленческих решений.
Временной ряд является одним из видов парной стохастической зависимости, в которой независимая переменная — время.
Исчисление показателей для анализа динамики в экономике позволяет оценить по временным рядам следующие показатели:
- Средний уровень. Он исчисляется из абсолютных уровней интервального или моментного временного ряда и называется средним хронологическим. И исчисляется по формуле:
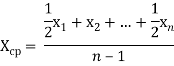 , (1)
, (1)
- Расчет темпа роста используется для того, чтобы показать, во сколько раз один уровень больше другого. При анализе использован цепной темп роста, т. е. произведено сравнение каждого уровня с предыдущим.
- Расчет абсолютного прироста могут исчисляться для каждого периода по отношению:
– к предыдущему периоду и характеризовать, например ежегодные абсолютные приросты;
– к начальному периоду и отражать накопленные абсолютные приросты.
- Расчет темпов прироста состоит в том, что абсолютный прирост делится на величину предыдущего (или начального) уровня, и выражается в процентах. Темп прироста характеризует, на сколько процентов увеличился рассматриваемый показатель за текущий период.
- Абсолютное значение одного процента прироста равно частному от деления абсолютного прироста на темп прироста и характеризует весомость одного процента в единицах уровня.
- Определение среднего темпа позволяет оценить интенсивность развития рассматриваемого явления за длительное время, которое характеризуется средним темпов. И вычисляется по формуле:
![]() =
= 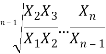 =
=![]() , (2)
, (2)
где
![]() - среднегодовой темп;
- среднегодовой темп;
n — период.
7. Оценка среднего темпа прироста ![]() выполняется по среднему темпу роста, выраженному в процентах, вычитанием 100 % или по среднему коэффициенту роста:
выполняется по среднему темпу роста, выраженному в процентах, вычитанием 100 % или по среднему коэффициенту роста:
![]() , (3)
, (3)
Основные задачи вычисления показателей временных рядов состоят в том, чтобы объективно охарактеризовать в развитии:
– направление и величину изменений от периода к периоду, т. е. от одной даты к другой дате;
– среднюю интенсивность процесса за исследуемые периоды;
– основную тенденцию динамики рассматриваемого процесса и возможность его прогнозирования.
Следующим этапом является сопоставление и анализ стохастически взаимосвязанных временных рядов и выполняется с помощью коэффициента опережения. Он показывает, во сколько раз один временной ряд растет быстрее другого, и определяется по отношению коэффициентов роста или темпов прироста двух рядов:
![]() , (4)
, (4)
где
![]() — меньший коэффициент роста;
— меньший коэффициент роста;
![]() — больший темп прироста;
— больший темп прироста;
![]() — меньший темп прироста.
— меньший темп прироста.
В прогнозировании используется большое количество различных методов. В практике наибольший удельный вес имеют методы, основы которых составляют статистико-экономические зависимости или производственные функции. В различных областях знаний и практике методы прогнозирования, базирующиеся на производственных функциях, занимают около одной трети от числа всех используемых в этих целях методов.
Прогноз (![]() ) в самом простейшем случае, когда средний уровень ряда не имеет тенденцию к отклонению, принимают равным:
) в самом простейшем случае, когда средний уровень ряда не имеет тенденцию к отклонению, принимают равным:
![]() =
= ![]() , (5)
, (5)
Это и будет уровень точечного прогноза. Но здесь целесообразно рассчитать погрешность средней и ее доверительные интервалы. Поэтому можно записать:
![]() ≤
≤ ![]() ≤
≤ ![]() +
+ ![]() , (6)
, (6)
где t — табличное значение t-критерия Стьюдента при n-1 степенях свободы и p-м уровне вероятности;
![]() — средняя квадратическая ошибка средней.
— средняя квадратическая ошибка средней.
Расчет средней квадратической ошибки
![]() =
= ![]() , (7)
, (7)
где ![]() среднее квадратическое отклонение, которое равно:
среднее квадратическое отклонение, которое равно:
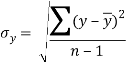 ,(8)
,(8)
Это и есть доверительный интервал в случае, когда предполагается, что уровень прогнозируемого показателя будет равен средней. Разумеется. Такой краткосрочный прогноз возможен лишь при условии, что исследуемый ряд близок к стационарному.
Литература:
- Гиляровская, Л. Т. Экономический анализ: Учебник для вузов [Текст] / Л. Т. Гиляровская. — М.: Юнити-Дана, 2006. — 615 с.
- Гришин, А. Ф. Статистические модели в экономике [Текст] / А. Ф. Гришин, С. Ф. Котов-Дарти, В. Н. Ягунов. — Ростов н/Д.: Феникс, 2005. — 344 с.
- Решение оптимизационных задач в экономике [Текст] / А. В. Каплан [и др.]. — Ростов н/Д.: Феникс, 2007. — 541 с.







