Рассматривается задача восстановления функции по наблюдениям со случайными ошибками. Причем, на стадии формулировки задачи отсутствует этап, связанный с параметрической структурой этой функции, в этой связи оценка ищется в классе непараметрической статистики, когда исходное описание функции неизвестно с точностью до вектора параметров. Особенностью данной задачи является то, что искомая функция описывается взаимно неоднозначной характеристикой и общепринятое непараметрическое оценивание оказывается непригодно. Понадобилось введение нового класса непараметрических оценок. Приводятся результаты некоторых вычислительных экспериментов.
Ключевые слова: априорная информация, непараметрическая модель, взаимно неоднозначные характеристики, непараметрические оценки
Введение. Рассматривается задача восстановления функции по наблюдениям, когда исследуемый процесс описывается взаимно неоднозначными характеристиками. Эта задача сводится к задаче аппроксимации, главной особенностью которой является отсутствие априорной информации о параметрической структуре модели исследуемого процесса. Предлагается непараметрическая оценка взаимно неоднозначных характеристик, ее некоторая модификация и результаты численных исследований.
При восстановлениифункций регрессии по наблюдениям часто используют непараметрические оценки. При этом предполагается, что характер ее зависимости однозначный по аргументу. Ниже рассматривается задача восстановления функции по наблюдениям при взаимно неоднозначной зависимости. Это потребовало внесения некоторых изменений в известную оценку Надарая-Ватсона.
Априорная информация. Априорная информация — совокупность заранее известных сведений об исследуемом процессе, критерии оптимальности и ограничениях. Критерий оптимальности является выразителем тех требований, которые должны быть наилучшим образом удовлетворены, а ограничения определяют наши возможности. Таким образом, априорная информация, известная исследователю на начальной стадии, является основой для математической формулировки задачи [1]. И по существу предопределяет, в значительной степени, метод исследования [2].
В различных компьютерных системах моделирования важная роль принадлежит восстановлению функций по наблюдениям, в частности взаимно неоднозначной функции, которые могут быть применены при создании, например, роботов, робототехнических систем при движении по заранее неизвестной местности (местности с неизвестным рельефом).
Уровни априорной информации имеют важное значение при моделировании и управлении дискретно-непрерывными процессами. К таким процессам относятся процессы, протекающие непрерывно во времени, но переменные, которых контролируются в дискретные моменты времени. Выделим следующие уровни априорной информации [3]:
‒ Системы с полной информацией. В этом случае оператор процесса точно известен, а случайные помехи, действующие на объект и каналах связи, отсутствуют. При решении задач идентификации и управления могут быть использованы методы математической теории оптимальных процессов, а также другие методы синтеза и анализа систем управления.
‒ Системы с неполной информацией. Это системы с независимым (пассивным) накоплением информации. В этом случае, влияние входного воздействия воспринимается как просто случайное воздействие. Помехи это обычно предполагаемое в теории стохастических систем случайное воздействие на объект. Кроме того, класс операторов не известен точно, но необходимы предположения о плотности распределения всех случайных факторов. Обычно плотности вероятности случайных факторов, действующих на объект и в каналах измерения переменных, предполагаются нормальными и аддитивными. Ясно, что в этом случае необходимо наличие выборки входных и выходных переменных объекта, а сами наблюдения являются статистически независимыми. Системы с неполной информацией относят к классу разомкнутых или нейтральных систем.
‒ Системы с активным накоплением информации. Особенность этих систем состоит в том, что задачи идентификации и задачи управления здесь могут быть объединены, потому что элементы выборки измерений поступают последовательно в обучающую модель и систему управления. Таким образом, в случае объединения этих задач выработка управляющих воздействий носит двойственный (дуальный) характер — они должны быть одновременно и изучающими, и управляющими [1,2]. Однако, если помехи, действующие на процесс, аддитивны и в каналах измерения, то в целом система дуального управления может быть приведена к разомкнутой, темп накопления информации у которой оказывается независимым от значений входных переменных. Такие системы называют приводимыми к разомкнутым или нейтральными. Но существует класс не нейтральных систем, т. е. класс неприводимых.
‒ Системы с параметрической неопределенностью. Параметрический уровень априорной информации предполагает наличие параметрической структуры модели и некоторых характеристик случайных помех, обычными из них являются нулевое математическое ожидание и ограниченная дисперсия. Для оценивания параметров используются чаще всего разнообразные итеративные вероятностные процедуры. При этих условиях также решается задача идентификации в узком смысле, как и во всех предыдущих случаях.
‒ Системы с непараметрической неопределенностью. Непараметрический уровень априорной информации не предполагает наличие модели, но требует наличие некоторых сведений качественного характера о процессе, например, однозначность, либо неоднозначность его характеристик, линейности (для динамических процессов) либо характер его нелинейности. Для решения задач идентификации на этом уровне априорной информации (идентификация в широком смысле [4]) применяются методы непараметрической статистики.
‒ Системы с параметрической и непараметрической неопределенностью. Важными с точки зрения практики являются задачи идентификации многосвязных систем в условиях, когда объем исходной информации не соответствует ни одному из вышеописанных уровней. Например, для отдельных характеристик многосвязного процесса на основании физико-химических и энергетических закономерностей, закона сохранения массы, балансовых соотношений могут быть выведены параметрические закономерности, а для других нет. Таким образом, мы находимся в ситуации, когда задача идентификации формулируется в условиях и параметрической, и непараметрической априорной информации. Тогда и модели представляют собой взаимосвязанную систему параметрических и непараметрических соотношений.
Непараметрический подход. Воснове этого подхода лежат непараметрические оценки плотности вероятности p(x) по наблюдениям 
, 
. Непараметрические оценки многомерной плотности вероятности подробно рассматривались в [5,6] и имеют вид:
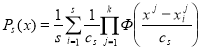, (1)
Где 
— оценка плотности распределения элементов, s — объем выборки, k — размерность вектора x.
Здесь Ф(v) — ядро — финитная колоколообразная интегрируемая с квадратом функция, удовлетворяющая условиям [3,5,6]
0 < Ф(v) < 
, 
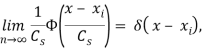(2)
— параметр размытости, определяющий размер носителя и «дельтаобразность» ядра Ф(v) [5,6]
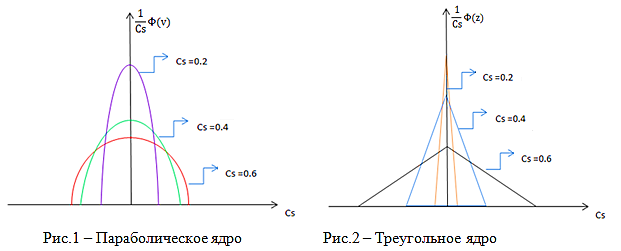
В вычислительном эксперименте используются колоколообразные функции Ф(v) различных видов, пример:
Прямоугольное ядро: 
(3)
Треугольное ядро:
Параболическое ядро:
На рисунках 1,2 представлена функция 
, построенная для трех значений параметра размытости = 0.2, 0.4, 0.6.
Параметр размытости удовлетворяет следующим условиям:
(4)
Непараметрическая оценка функции регрессии по наблюдениям. Для восстановления функции регрессии M
по наблюдениям 
используем непараметрические оценки плотности вероятности (1). Поскольку, M выглядит следующим образом:
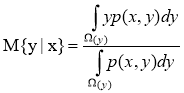. (5)
Заменяя в (5) p(x,y) непараметрическими оценками (1) и используя свойство:
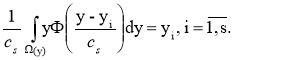. (6)
легко получить непараметрическую оценку функции регрессии Надарая-Ватсона, которая для одномерного случая выглядит следующим образом:
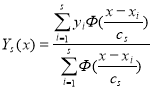, (7)
а для случая, если x k-мерный вектор равна:
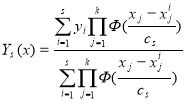, (8)
где 
выборка наблюдений, 
— колоколообразная функция, v — произвольная переменная, 
— параметр размытости.
При восстановлении взаимно неоднозначной функции регрессии оценка Надарая-Ватсона должна быть изменена следующим образом:
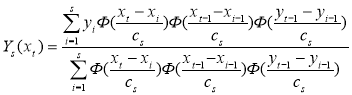, (9)
где 
, 
значения координат функции регрессии на предыдущем шаге ее оценивания [7].
Как показали многочисленные вычислительные эксперименты целесообразно (7) несколько подкорректировать следующим образом:
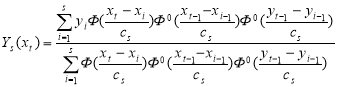, (10)
где 
с точностью до коэффициента повторяет 
, а 
= 1, если 
< 1 и 0 в остальных случаях. В этом случае 
не будет влиять на ошибку восстановления, но позволит «зафиксировать» алгоритм в предыдущей точке движения при оценивании каждой последующий точки.
Вычислительный эксперимент. При проведении вычислительного эксперимента взаимно неоднозначные характеристики могут иметь различную форму: окружности, эллипсов и другие. Без нарушения общности, взаимно неоднозначную характеристику примем в дальнейшем в виде окружности.
, (11)
где 
- радиус окружности.
В этом случае обучающая выборка формировалась следующем образом: произвольно задавалась начальная точка 
и при принятом значении радиуса вычислялись значения 
. В итоге, формировалась выборка 
. Обратим внимание на то, что 
могли быть определены в результате равномерного шага 
по x
или датчика случайных чисел 
, 
.
При восстановлении взаимно неоднозначной характеристики по наблюдениям, которое исследователю неизвестно, важным является вопрос о выборе направления движения, хотя в принципе оно может быть произвольным на начальной стадии. Зато все последующие изменения текущей переменной х находятся в строгой зависимости от предыдущего.
Процессы, характеризуемые взаимно неоднозначными зависимостями, имеют такую особенность, что выборочные значения появляются строго последовательно. На рис. 3 представлен такой процесс. Появление выборочных значений начинается в некоторой точке 
и двигается последовательно, проходя точки 
, 
, …. При этом, переход из точки t в точку 
невозможен, пока не будут пройдены промежуточные четыре точки.
Таким образом, существо предложенных оценок (9,10), заключается в том, что при оценивании очередной точки, производится «фиксация» предыдущей точке в соответствующих алгоритмах (9,10).
На рис. 3 представлен процесс, представляющий собой окружность. Движение по переменной х происходит справа налево и слева направо, что характеризует последовательное появление выборочных значений.
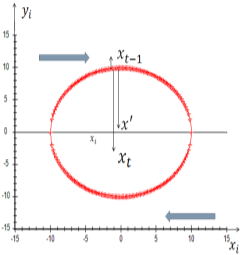
Рис. 3. Представлена данная выборка
На следующем шаге добавлялось случайное воздействие 
на наблюдения 
.
, (11)
где 
, уровень помех 
В качестве критерия точности непараметрической оценки использовалось соотношение:
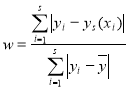, (12)
где 
- среднее арифметическое; 
— непараметрическая оценка; 
– истинная выборка, полученная по формуле (11).
Приведем результаты численного исследования, иллюстрирующие эффективность алгоритма.
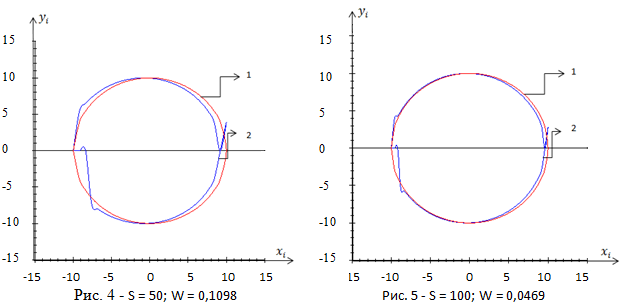
В качестве колоколообразной финитной функции использовалось треугольное ядро. Алгоритм тестировался на обучающих выборках различного объема, при этом последовательное увеличение объема выборки производилось путем добавления новых элементов к уже имеющимся: s = 50, 100, 500.
Обозначим на всех рисунках цифрой (1) — обучающую выборку, (2) — непараметрическую оценку.
Продемонстрирована работа алгоритма (9) на рисунках 4, 5, 6 в различных условиях: когда объем выборки равен 50, 100, 500 элементам; уровень помех равен 0 %; эксперимент проводился в режиме скользящего экзамена.
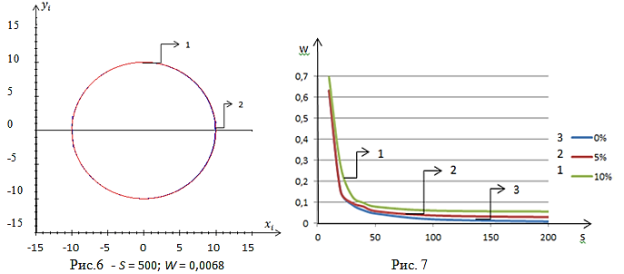
На рисунке 7 представлена зависимость значений ошибки восстановления от объема выборки при различных уровнях помех.
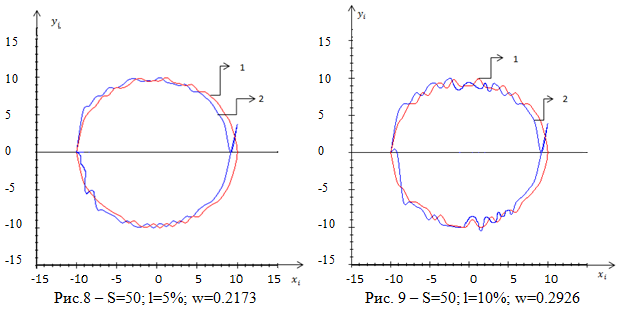
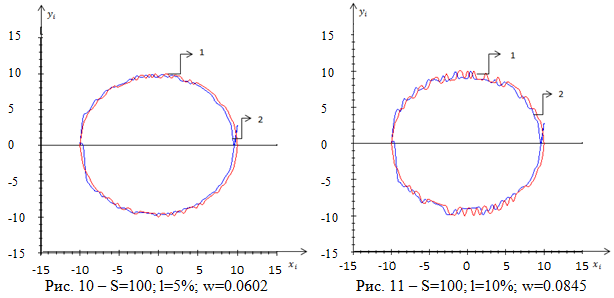
На рисунках 8–11 хорошо видно, как зависит ошибка восстановления от уровня помех и от объема выборки.
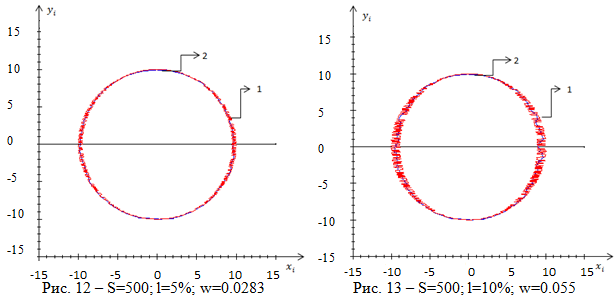
Для наглядности, поменяем в оценке (9) местами 
и 
рисунки 12, 13. Убедимся в том, что оценка несколько отличается в местах пересечения графика с осью абсцисс, как могло показаться из рисунков 8–11.
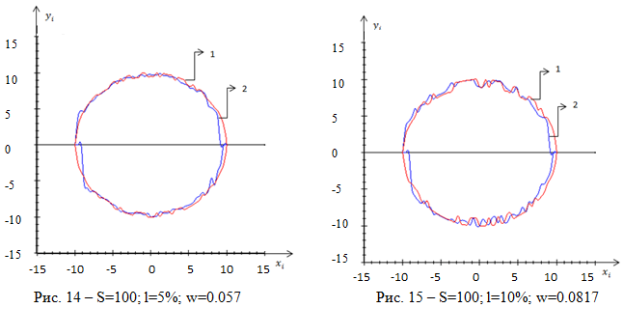
Продемонстрируем работу модифицированного алгоритма (10), в следующих условиях: при уровне помех равном 5 % и 10 %; с объемом выборки равным 100 элементам; в режиме скользящего экзамена. Сравнивая ошибки восстановления см. рис.10–11; рис. 14–15, видим небольшое улучшение.
На рисунках 14–15 видим, что ошибка восстановления немного меньше, чем на рисунках 10–11. Значит и непараметрическая оценка стала точнее.
Следует отметить, что: с уменьшением ошибки восстановления (
), точность оценки возрастает; с ростом объема выборки (s), ошибка восстановления (
) уменьшается; величина ошибки растет, при возрастании уровня помех (l).
Возможно, возникнет вопрос: «Почему для проверки работы алгоритма использовалась окружность?», ведь так много более сложных фигур, а ответ прост — особенностью данного алгоритма является его универсальность. Это значит, что алгоритму не принципиально какую функцию восстанавливать, будь то окружность, эллипс или спираль Архимеда. Закрепляясь в какой-то точке и выбирая направление обхода, всегда можно получить непараметрическую оценку взаимно неоднозначных функций.
Заключение. Основной результат настоящей статьи состоит в введении нового класса непараметрического оценивания взаимно неоднозначных функций по наблюдениям с ошибками. Это отличает задачи непараметрического оценивания от известных непараметрических оценок функции регрессии Надарая-Ватсона. Приводятся некоторые модификации непараметрических оценок, в таких условиях обращается внимание на методику обхода введенных непараметрических оценок по траектории, определяемой элементами обучающей выборки.
Для простоты численного исследования была взята функция, описываемая окружностью, хотя это не является существенным для предложенного алгоритма. Иными словами, предложены алгоритмы, пригодные для восстановления неоднозначных зависимостей, описываемых более сложными кривыми, характер которых априори неизвестен, известна лишь: выборка наблюдений исследуемого процесса.
Огромная благодарность выражается нашему научному руководителю Медведеву Александру Васильевичу за постоянную поддержку и труд, вложенный в нас.
Литература:
- Фельдбаум А. А. Основы теории оптимальных автоматических систем. Москва. Изд. Физматгиз, 1963 г. —552 с.
- Цыпкин Я. З. Адаптация и обучение в автоматических системах. Изд. ≪Наука≫, 1968 г. — 400 с.
- Медведев А. В. Основы теории адаптивных систем. Красноярск, 2015. — 526 с.
- Эйкхофф П. Основы идентификации систем управления. М.: Мир, 1975. — 683с
- Надарая Э. А. Непараметрическое оценивание плотности вероятностей и кривой регрессии //Тбилиси: Изд-во Тбил. ун-та. — 1983.
- Васильев В. А., Добровидов А. В., Кошкин Г. М. Непараметрическое оценивание функционалов от распределений стационарных последовательностей. — М.: Наука, 2004.
- Живоглядов, Медведев А. В., Тишина Е. В. Восстановление неоднозначных статических характеристик по экспериментальным данным // Автоматизация промышленного эксперимента. Фрунзе 1973г. с.32–39.
