В наблюдаемой области Вселенной очевидна иерархическая структура и упорядоченность расположения бесконечного ряда величин масс, которые, являясь центральными для масс спутников в собственном гравитационном поле, в свою очередь, являются спутниками в гравитационных полях еще больших центральных масс. Поэтому гравитационное поле любого тела искривляет не просто пространство, а меняющееся гравитационное поле определенного интервала центральной массы. Известно, что на разном энергетическом фоне центральной массы в зависимости от особенностей интервала движение тела различно, поэтому и его гравитационное поле также должно быть разным и переменным. Это обуславливает необходимость понять влияние переменного гравитационного поля интервала центральной массы на существующие в нем массы и их поля.
Одной из характеристик неоднородности гравитационного поля массы является кривизна интервала, в формулу которой входит эксцентриситет (е), отражающий его геометрические свойства:
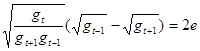 ,
,
где g t-1 < g t < g t+1 напряженности границ и среднего радиуса интервала от геометрического центра массы в соответствующие моменты времени t.
При учете знака эксцентриситет показывает долю и направление относительных изменений среднего радиуса поля каждой из противоположных сторон центральной массы за полупериод и зависит как от напряженности поля в интервале 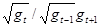 , так и от скорости ее изменения ±
, так и от скорости ее изменения ±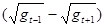 - относительного ускорения. Ранее был представлен анализ одного из возможных проявлений геометрических свойств переменного гравитационного поля - образования последовательности приливных волн, согласующейся с закономерностью Тициуса - Боде. При этом поляризация (приливное неравенство) приливной волны сопряжена с разницей величин и направлений относительных ускорений на разных сторонах центральной массы. Показана принципиальная возможность закономерной суперпозиции приливных волн в любой точке гравитационного поля и их влияния на центральную массу [1]. Практически не исследованными геометрическими свойствами, обусловленными скоростью и направлением изменения напряженности гравитационного поля, являются особенности относительных ускорений в интервале, связанные с изменением плотности его энергии.
- относительного ускорения. Ранее был представлен анализ одного из возможных проявлений геометрических свойств переменного гравитационного поля - образования последовательности приливных волн, согласующейся с закономерностью Тициуса - Боде. При этом поляризация (приливное неравенство) приливной волны сопряжена с разницей величин и направлений относительных ускорений на разных сторонах центральной массы. Показана принципиальная возможность закономерной суперпозиции приливных волн в любой точке гравитационного поля и их влияния на центральную массу [1]. Практически не исследованными геометрическими свойствами, обусловленными скоростью и направлением изменения напряженности гравитационного поля, являются особенности относительных ускорений в интервале, связанные с изменением плотности его энергии.
Оценка любых геометрических изменений поля возможна только в совокупности близкорасположенных пробных частиц, составляющих отрезок, плоскость или объем. Эти геометрические изменения являются результатом неоднородности энергии гравитационного поля в области пробных частиц при их одновременном движении относительно центральной массы или неподвижности относительно нее в переменном гравитационном поле. В системе отсчета, связанной с геометрическим центром центральной массы, каждая частица отражает локальное ускорение свободного падения, с которым неизбежно сопряжены относительные ускорения изменений расстояний между частицами. Центральная симметрия гравитационного поля позволяет оценивать самое простое движение – динамику относительных расстояний в паре пробных частиц. Две частицы А и D находятся на расстоянии lг (1r << R) одной эквипотенциальной поверхности радиуса R массы М с центром в т.О. При одновременном свободном движении по своим вертикалям с ускорением а через интервал времени ∆ t частицы сближаются с горизонтальным относительным ускорением а г , которое равно сумме двух проекций общего ускорения на 1г, (рис.1а). Из подобия прямоугольных треугольников находим относительное ускорение сближения частиц а г (противоположно направленное движение с уменьшением относительного расстояния обозначим «-») [2].
а г = - а 1г/R
Пробная частица С находится на одной вертикали, но дальше от А на расстоянии от нее 1в = АС. Напряженность в А g А = - j M/(R)2 , j – гравитационная постоянная . В соответствии с биномом Ньютона, g C = - j M/(R + l в )2 = - j MR -2 (1+ 1в/R)-2 = j M R -2 [1-2 1в/R + 3 (1в/R)2 -...]. Если учесть, что расстояние между пробными частицами много меньше расстояния до тяготеющей массы, то можно пренебречь всеми членами разложения, кроме первых двух. Вычитая ускорение в С из ускорения в А получаем, что относительные ускорения между точками противоположно направлены, а расстояние между точками возрастает (изменяется противоположно горизонтальному), поэтому относительное вертикальное ускорение
а в = 2 а 1в/R .
.
Если в начале движения пробных частиц без начальной скорости зафиксировать их одновременно падающий геометрический центр (начало собственной системы координат), то по отношению к нему выявляется поляризация в системе пробных частиц. Поскольку кривизна поля М в 1-2 меньше, чем в 3-4, то и относительные ускорения в области 1-2 меньше, чем в 3-4.
|
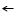
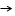
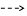

|


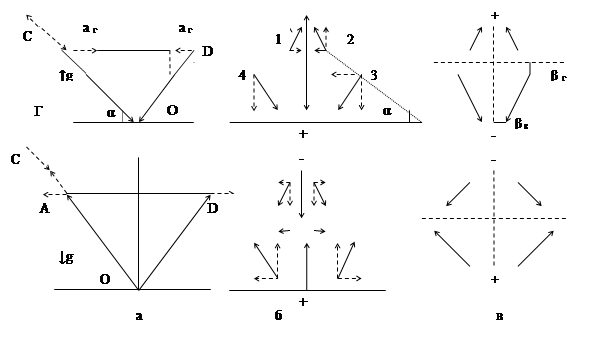
Рис. 1.Относительные ускорения пробных частиц в интервале поля центральной массы.
А, Д ,С пробные частицы, обозначения верхнего и нижнего рисунков совпадают; стрелками показаны направления относительных ускорений, В и Г- вертикальная и горизонтальная оси системы координат, связанной с геометрическим центром О массы М. а. А и D на одной эквипотенциальной поверхности, А и С – на одной вертикали при возрастании (вверху) напряженности (↑g) поля и при ее уменьшении (внизу). б. Сплошными стрелками показаны равнодействующие ускорения в системе 4 частиц, расположенных в углах трапеции, на разном расстоянии от О, пунктиром – их вертикальные и горизонтальные проекции в системе координат, связанной с частицами. в.предполагаемые изменения относительных расстояний между частицами в их системе координат (пунктир).
Поэтому при возрастании напряженности ближе к центральной массе будет А - полупространство («-», полупространство апогелия), а дальше от центральной массы – П («+», полупространство перигелия). При уменьшении напряженности ближе к центральной массе будет П - полупространство, а дальше – А. В рассмотренных случаях пробные частицы находились либо на одной эквипотенциальной поверхности, либо на одной вертикали. В общем случае, линии, соединяющие частицы, могут иметь любой угол по отношению к осям системы координат, связанной с центром тяжести М. Для близкорасположенных частиц можно построить прямоугольные треугольники из расстояний l = 1-4 = 2-3 и их вертикальных (1в) и горизонтальных (1 г) проекций, вдоль которых действуют относительные ускорения а в и а г. Результирующее относительное ускорение между частицами а 1 находим по теореме Пифагора
а1 = ( аг2 +а в2)0,5 = [ а 1 ( 1+ 3 sin2 α)0,5] /R,
где α – угол наклона 1 к горизонтальной оси координат (рис.1а, б),
l г = l cos α, 1в =1 sin α , a г = - a l cos α /R , a в = 2 a l sin α /R .
Тогда интервалу l будет соответствовать кривизна
К1 = а 1/ 1 = [а ( 1+ 3 sin2 α)0,5 ]/R
Если α = 0о, то К1 = Кг = -а/R, если α = 90о К1 = Кв =2а/R. В системе координат, связанной с пробными частицами, расстояние между частицами соответствует интервалу (диаметру) в системе координат, связанной с М. Поэтому радиусу R, соответствует расстояние
0,5 l = r. Тогда относительное горизонтальное ускорение для этого расстояния (полуинтервала) аг = - а 1г / 2R, Kг = -a/2R , а относительное вертикальное ускорение
а в = а 1в/R, Кв = а в = а /R , (рис.1). Рассмотренная ранее кривизна является вертикальной для расстояния R интервала K = К в = 4e/∆ t2 = 4 ∆R/ R ∆ t2 = 4 a ∆ t2 /4R ∆ t2 = a/R, тогда горизонтальная кривизна Кг = - 2е/∆ t2 = - a/2R , [1]. Таким образом, кривизна поля интервала, расположенного на расстоянии среднего радиуса от геометрического центра массы М по отношению к ней, и кривизна поля внутри этого интервала по отношению к системе координат, связанной с пробными частицами, одна и та же величина.
Кривизна по направлению расстояния между двумя пробными частицами обуславливает относительное ускорение между ними и по теореме Пифагора превышает вертикальную К = ± К в √ 1,25 = 1,118 К в . Отличие периода (Т= π ∆ t /√ е) от времени изменения напряженности (∆t) в интервале означает, что обращение естественного спутника вокруг центральной массы является следствием относительного ускорения , т.е. отражает геометрические свойства интервала. Кривизна (К) создает тангенциальное ускорение (aτ) и тангенциальную скорость(Vτ = a τ ∆ t = (4,472 e2 R)/∆ t ), изменяющую среднюю скорость (Vcp = Rср √Kср ) движения на орбите ( «+» в П - полупространстве и «-» в А – полупространстве). Тогда скорость в полупространстве (V):
V = Vср ± Vτ = Vcp ± (4,472 e2 R)/∆ t , (табл.1).
Таким образом, тангенциальное ускорение одновременно геометрически обуславливает скорость и соответствующую ей траекторию движения, которую можно рассматривать как круговую по отношению к фиктивной массе. Очевидно, что реальный центр тяжести будет менять свое положение в собственном сложнопериодическом гравитационном поле.
Если поместить твердое тело (стержень) в положение точек 1-3, то при возрастании напряженности в вертикальной плоскости центральной массы оно приобретает вращательный момент по часовой стрелке (рис. 1в, вверху), который может сохраниться и при уменьшении напряженности, если стержень займет положение 2-4 (рис.1в, внизу). При периодическом смене направления изменения напряженности, тело может вращаться в одном направлении вокруг оси, перпендикулярной плоскости расположения частиц.
Связь кривизны с множителем (1+ 3 sin2 α)0,5 показывает зависимость относительных ускорений между пробными частицами от направлений соединяющих их отрезков к осям системы координат, связанной с М. Максимум относительных ускорений имеет расположение при α=45о, создающее преимущество относительных смещений частиц. По отношению к системе координат, связанной с центральной массой, траектории относительных движений частиц направлены под определенными углами к вертикали и горизонтали (углы β) (рис.1 в):
tg β г = ∆lв/∆l г
При α=45о, горизонтальные и вертикальные проекции отрезка 1 одинаковы, как радиусы окружности. Поэтому удобно рассмотреть положения и величины относительных расстояний 1 при изменении исходно равных отрезков (цены деления) вертикальной и горизонтальной осей собственной системы координат при возрастании и уменьшении напряженности. При возрастании напряженности поля цена деления вертикальной оси будет возрастать в 2 раза быстрее, чем уменьшаться на горизонтальной оси. Тогда (tg β г = 2), β г = 63о27’ , β в = 26о33’, а траектории относительного движения частиц к вертикали будут направлены так, что их продолжения пересекутся в пространстве, образуя вершины конусов траекторий с углом при вертикали 53о 06’, а при горизонтальной плоскости 126о 54’ (рис.1в, вверху). Отсюда изменение относительного расстояния ∆l = 1,118 √ ∆lв . При уменьшении напряженности цена деления вертикальной оси уменьшается в 2 раза быстрее, чем возрастает по горизонтальной оси, поэтому (tg β г = 1/2). Траектории относительных движений частиц направлены противоположно: β г = 26о33’ , β в = 63о27’, при пересечении образуют конусы с углом при вертикали 126о 54’, а при горизонтальной плоскости 53о 06’(рис. 1в, внизу). Изменение относительного расстояния ∆l = 0,5 1,118 √∆lв. Очевидно, что исходная форма однородной области, занятой неподвижными пробными частицами, при периодическом изменении напряженности начнет периодически изменяться: возникнут стереотипно направленные ускоренные потоки частиц, неоднородность концентраций, зависимость движений от относительных расстояний, эволюционирует форма и др.
Существенным результатом является равенство величин кривизны поля в интервале (К 1) и его кривизны по отношению к центральной массе (К): К1 = К. Согласно существующим представлениям, гравитационное поле центральной массы на расстоянии полуинтервала R – это градиент энергии М к энергии интервала. Если поместить в начало системы координат, связанной с пробными частицами в интервале, массу m, то все рассуждения можно отнести и к этой массе. Тогда гравитационное поле массы m, расположенной в интервале, – это градиент ее энергии к энергии этого же интервала. Значит величины относительных ускорений в одном и том же интервале будут зависеть только от масс на соответствующих им относительных расстояниях:
j M/ [R3(1-e2)] = j m/ [r3(1-e2)] = j m/[(nR)3(1-e2)],
где n – показывает отличие характеристик m и ее поля от центральной массы М и ее поля. Масса m спутника через кривизну интервала связана с центральной массой М, обусловившей для нее фоновое гравитационное поле, поэтому m = М n3 , а m = n а, r = n R. Результаты оценки радиусов и ускорений минимальной (фоновой) кривизны собственных полей планет представлены в табл.1. Энергии (Е) этих масс на соответствующих расстояниях будут связаны
Е m/ЕM = (m/M)2/3 = n2.
Если предположить, что масса спутника пассивно движется в интервале центральной массы за счет его геометрических изменений, то она оказывается в поле периодически изменяющейся кривизны. Соответственно эксцентриситету, радиус интервала собственного гравитационного поля спутника m будет меняться с той же закономерностью, как и радиус соседней внутренней приливной волны центральной массы M, т.к. этот интервал является фоном и для нее [1]. Поэтому при возрастании напряженности фона полупространства возникают приливные волны А – полярности, а при уменьшении напряженности – П - полярности. Тогда и собственное поле спутника будет изменяться подобным образом, а приливные неравенства в нем будут обусловлены не только интервалом, но и его массой. В определенных условиях (например, формирования или разрушения) величина массы спутника может оказаться не случайной, а зависимой от центральной массы и интервала.
Таблица 1.
Расчетные значения радиусов (r) и ускорений (a) приливных волн фоновой
кривизны (интервала орбиты) гравитационных полей масс планет.
Название R1011,м К R,с-2 a, м/с2 Vτ 103, м n 10-2 r , м а m ,м/с2
Меркурий 0,58 68,01 10-14 4,94 10-2 9,450 0,60 0,35 109 0,023 10-2
Венера 1,08 10,50 10-14 1,13 10-2 0,044 1,34 1,45 109 0,015 10-2
Земля 1,49 3,96 10-14 59,80 10-4 0,143 1,44 2,16 109 0,855 10-4
Марс 2,28 1,11 10-14 26,60 10-4 1,490 0,69 1,60 109 0,178 10-4
Юпитер 7,78 0,28 10-15 2,20 10-4 0,310 9,85 7,68 1010 0,214 10-4
Сатурн 14,30 4,4910-17 0,65 10-4 0,283 6,59 9,44 1010 0,042 10 -4
Уран 28,70 5,58 10-18 1,60 10-5 0,155 3,54 1,02 1011 0,569 10-6
Нептун 45,00 1,39 10-18 6,50 10-6 0,010 3,73 1,68 1011 0,234 10-6
Плутон 59,00 0,65 10-18 3,80 10-6 1,296 1,41 0,83 1011 0,054 10-6
Жирным шрифтом обозначены характеристики орбиты:
R - средние расстояния орбитальных интервалов от Солнца
KR = a/R - кривизна поля орбитальных интервалов (а ~ g)
a ~ g - напряженность на расстояниях R
n = 3√m/M
В поле массы при е ≠ 0 одновременно существуют два фоновых полупространства разных знаков. Анализ направлений относительных ускорений в полупространствах фона при возрастании напряженности гравитационного поля центральной массы показывает, что силовые линии «растягиваются» по вертикали к вершине конуса траекторий, образуя угол примерно 53о и сжимаются по горизонтальной плоскости с углом 127о (рис. 2б, внизу). При уменьшении напряженности силовые линии «сжимаются» по вертикали конуса под углом 127о и растягиваются в горизонтальной плоскости с углом 53о (рис.2б, вверху). Суммарный угол при горизонтальной плоскости σ = 90о. Т.о., фоновый орбитальный интервал соответствует минимальной кривизне собственного поля спутника и образует приливную эллиптическую волну, которая, в свою очередь, становится фоном для 2-х симметричных приливных волн примерно с периодом ~0,5 ее периода, и далее согласно закономерности Тициуса-Боде (рис. 2в) [1]. По-видимому, реальное изменяющееся гравитационное поле интервала при свободном падении тела, обращении в интервале орбиты или в состоянии неподвижности относительно системы координат, связанной с центральной массой, является фоном для его массы и обуславливает переменность его собственного гравитационного поля. Это свидетельствует в пользу представления о любом гравитационном поле, как переменном, а о любой массе, как частице-волне (массе - приливной волне).
В приливной волне определенной кривизны К (периода) можно выделить ее орбитальную часть, где ускорение соответствует центральной массе, и радиальную часть, где при такой же кривизне на других расстояниях относительное ускорение линейно связано с относительным расстоянием. Поэтому на расстояниях, меньших среднего радиуса орбиты, это ускорение меньше и соответствует некоторой меньшей фиктивной массе. В радиальной ее части на расстояниях, превышающих орбитальное, ускорение и радиус при сохранении кривизны возрастают и соответствуют большей фиктивной массе. В результате суперпозиции на орбитах далеких от Солнца планет должны присутствовать и колебания с периодами орбит внутренних планет. В фрагменте орбиты Нептуна за 1991-1993 гг. существуют колебания кривизны по расположению экстремальных точек и среднему периоду, близкие к орбите Венеры.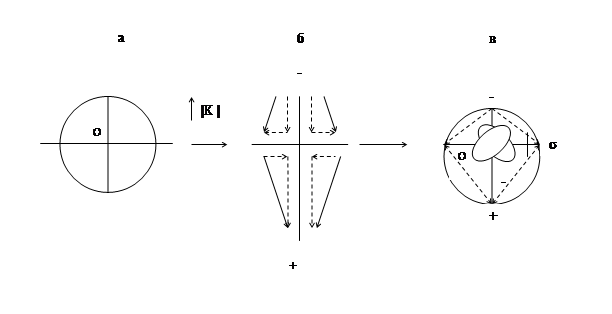
Рис. 2. Относительные ускорения в поле противоположных сторон массы при изменении кривизны интервала.
Формы эквипотенциальной поверхности поля радиуса r массы спутника m с геометрическим центром О при: а. е = 0 ; б. стрелки показывают относительные ускорения изменения радиуса при возрастании абсолютной величины кривизны |K| интервала в зависимости от знака полупространств фона («-», «+» ); в. поляризация поля m при максимальном е ( «-» , «+») и 2-е внутренние приливные волны противоположной полярности («+» вверху, «-» внизу).
Если ускорение и радиус приливной волны связаны с центральной массой, то ее можно назвать основной, а если ускорение и радиус приливной волны относятся к фиктивной массе, то – модулирующей (колебания орбиты Нептуна с периодом орбиты орбиты Венеры являются моделирующими). Наличие модулирующих колебаний в любых точках гравитационного поля ставит вопрос о скорости распространения приливной волны. Если считать, что она соответствует скорости света, то для волны определенного периода существует предельное расстояние, на которое она может распространиться. Например, за период орбиты Венеры расстояние распространения волны R c = c ∆ t = 1,5 10 14 м, т.е приливная волна ее орбиты должна не только влиять на Солнце, но и иметь место на орбитах планет и более долгопериодных приливных волн.
В результате сложнопериодного действия относительных ускорений (приливных волн) собственного гравитационного поля любая масса в пределах ее размеров подвергается относительным движениям и изменениям, совершая работу (А). Одинаковая работа по деформации, формообразованию и разрушению массы М может совершаться за небольшое время при большом ускорении или при малом ускорении и длительном интервале времени
А = [М (а ∆t)2]/2.
Одной из иллюстраций возможности влияния относительных ускорений на массу является изменчивость кометы [3]. В строении и изменении массы и формы есть особенности, которые могут быть следствием динамики ее собственного гравитационного поля. Движение комет вокруг Солнца происходит внутри сферы, диаметром порядка 1015 м, поэтому можно предположить, что, подобно планетной, существует кометная система приливных волн, соответствующая закономерности Тициуса-Боде, а само обращение вокруг Солнца связано с изменением направления напряженности фона [1]. Возможно 4 вида таких движений комет в орбитальных частях этих волн: при возрастании и уменьшении напряженности в фоновых интервалах в П- и А- полупространствах поля Солнца. Вследствие значительных эксцентриситетов, большая часть обращения кометы происходит в А - полупространстве ее орбиты, где ускорение движения аА = g/(1-e2А), (табл.2), поэтому и период ее обращения связан, в основном, с ним.
В точке среднего радиуса (е=0) орбиты кометы граница ее собственного поля обусловлена, в основном, массой и практически является окружностью. При приближении к Солнцу, возрастает напряженность поля, обуславливающая фоновую кривизну собственного поля кометы. Наличие «хвоста» показывает, что масса и средний радиус приливной волны минимальной кривизны уменьшаются, а ускорение ее поля и относительные расстояния между частицами возрастают. Частицы «хвоста», соответственно относительным ускорениям, расходятся: в направлении Солнца больше, образуя А-полупространства, чем с противоположной стороны (П - полупространства). С.В. Орлов обнаружил, что наибольшие ускорения расхождения частиц от ядра происходит с концов, удаленных от него (проявляется зависимость относительных ускорений от расстояний). «Оболочки» в области головы кометы могут свидетельствовать о расслоении собственного гравитационного поля кометы на внутренние приливные волны, действие которых усиливает разрушение ядра (чему способствует и более высокая температура). Относительные ускорения 2-х внутренних приливных волн собственного гравитационного поля ( рис. 1в, вверху, и 2в) в результате суперпозиции могут проявить себя в эллиптичной форме полупространства хвоста кометы в виде 2-х симметричных впадин при противоположной поляризации и двух выступов при одинаковой. При удалении от Солнца «хвост» кометы (m) уменьшается, что может быть связано с уменьшением напряженности поля Солнца (М) и изменением направления относительных ускорений расхождения на противоположное (рис.1в, внизу).
В таблице 2 показаны вертикальные ускорения поля орбиты и связанные с интервалом орбиты характеристики поля кометы Энке-Баклунда, n = 2,154 10-5 . За полупериод приливной волны орбиты собственное поле кометы фоновой кривизны, которому соответствует Т = 3,28 года, ∆ t = 1,606 10 7 c, частицы «хвоста» проходят со средним ускорением 0,94 10-7 м/с2 , ∆r = 6,055 106 м . Для расчета относительных изменений диаметра поля кометы были взяты средние характеристики: при возрастании напряженности поля Солнца вертикальное изменение диаметра 12,13 107 м, которое при сложении с его средним значением составляет 19 км. При уменьшении напряженности (движении от Солнца) аналогичное расстояние примерно 10 км. Реально большие размеры (порядка 109 -1011 м), обозначенные частицами «хвоста», возможно, связаны с их распространением вместе с приливными волнами ее собственного гравитационного поля, которые могут проходить расстояние Rc = c ∆t = 4,818 1015 м. При этом каждая частица-волна «хвоста» кометы должна испытывать сложные движения и изменения своего поля
Таблица 2.
Некоторые характеристики орбиты и собственного поля кометы Энке-Баклунда
Положение R 1011 g R 10-2 e a R 10-2 r 106 g r 10-7 a r 10 -7
ПR 0,497 5,3736 Пr 1,071 11,5747
RП 1,903 0,3665 0,7387 0,8067 rП 4,112 0,7894 1,7376
R 3,308 0,1213 0,8498 0,4366 r 7,125 0, 2613 0,9404
RА 4,714 0,0597 0,2984 0,0655 rА 10,154 0,1286 0,1411
AR 6,119 0,0355 Ar 13,180 0,0765
* Масса m = 2 1016 кг.
Обозначения: R , м - расстояния перигелия (П), апогелия (А) и среднего радиуса орбиты; r - такие же расстояния поля кометы минимальной кривизны и все обозначения для него; g и a , м/с2 , – напряженности и ускорения, е – эксцентриситеты орбиты (R) и ее П- и А-полупространств.
(своего рода, сопротивление) в поле Солнца, которые уменьшают расстояние их распространения. Движение кометы в области перигелия своей орбиты с ускорением а П = g/(1-e2П) имеют аналогичные, но значительно большие изменения, о чем свидетельствует разрушение ее ядра, однако на близком расстоянии от Солнца, вследствие высокой температуры, изменения поля комет не обозначаются частицами ее массы.
Относительные движения меняют и, в конечном счете, разрушают массу, но темп ее разрушения будет зависеть не только от вещества массы, его состояния и условий, но и от кривизны (эксцентриситетов) приливных волн собственного гравитационного поля. Если этот процесс заметен для наблюдателя, то процесс разрушения может отразить характерные для относительных ускорений геометрические особенности: слоистость, углы конусов траекторий, суперпозицию приливных волн (разрушение через формообразование) и др. Значимость долгопериодной динамики относительных ускорений гравитационного поля для массы можно увидеть в форме Земли, ее континентов и океанов. В ряде специальных исследований причиной геологических изменений Земли и ее живой природы рассматриваются колебания энергии ее гравитационного поля [4,5,6]. Земная кора непрерывно испытывает изменения, которые носят неравномерный периодический характер – наблюдаются чередования более интенсивных движений и их замедлений. Движения разных континентов могут быть синхронными. Возвышение материков и снижение уровня океанов чередуется с их погружением в расширяющиеся водные бассейны. По-видимому, дрейф и формообразование материков происходит под действием собственного поля Земли, изменяющегося в ответ на суммарное влияние приливных волн как Галактического, так и Солнечного интервалов. Поскольку южное полушарие Земли обращено к центру Галактики, то, при возрастании напряженности поля галактического интервала, масса Земли может перераспределиться с севера на юг (рис. 1в, вверху), что также отражается заостренностью формы материков южного полушария (рис.4).Скорость колебательных движений составляет, в основном, доли сантиметров в год [7]. Относительные ускорения переменного гравитационного поля Земли совершают работу как по движению и формообразованию ее массы, так и динамике подвижных сред (атмосферы и гидросферы). Если эта работа продолжается в течение Галактического года при эксцентриситете ( е = 0,15) T = 200 млн. лет = 6 1015 с, кривизне галактического интервала К = 10-30 с-2 , то для среднего расстояния толщины коры Земли (∆R = 30 км) скорость относительного движения V = а ∆t = K ∆R ∆t = 2,2 10 -11 м/с = 0,7 мм/год, а для радиуса Земли около 5 см/год.
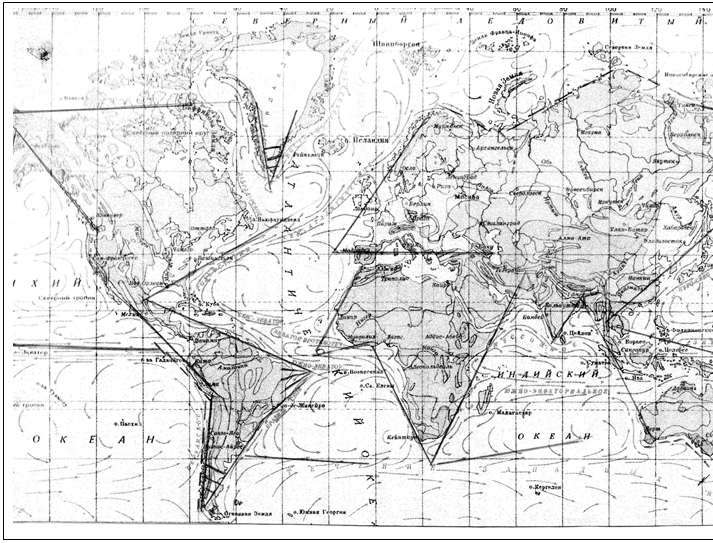
Работу поля по формообразованию Земли, в течение миллиардов лет с периодом Галактического года и иерархической лестницей периодов приливных волн, начиная с геологического ( порядка 60-80 млн. лет), можно обнаружить на глобусе. При этом сами материки, по-видимому, имеют собственные сложные периодические гравитационные поля, следствием приливных волн которых могут являться движения воды в виде течений, разломы и границы с повышенной сейсмической и вулканической активностью. Например, в области Мексиканского залива находится точка пересечения конуса траекторий приливной волны, где относительные ускорения имеют максимальное значение. В орбитальных частях таких приливных волн могут также быть циркуляционные или вихревые движения воды и воздуха. В крупном плане глобусов и карт в форме континентов и океанических течений наиболее часто встречаются углы, характерные для «конусов траекторий»: примерно 53о , 127 о , 27о , и 63о (рис.4). На глобусах разного масштаба эти углы выражены с разной четкостью, однако их наличие очевидно.
Таким образом, градиент энергии гравитационного поля проявляется в ускоренном движении тел относительно центральной массы. Однако, неизбежно сопряженной с изменением поля, является плотность его энергии, которая геометрически выражается в динамике относительных расстояний силовых линий и эквипотенциальных поверхностей. Адекватной оценкой этой стороны гравитационного поля является кривизна его интервала, на основе которой можно рассчитать все характеристики относительных движений, отражаемые массами пробных тел.
Сделано предположение, что основой механизма взаимодействия гравитационного поля и массы тела, является энергия интервала, общая как для центральной массы, так и для массы тела. Отличие характеристик полей масс обусловлено отношением их величин. Периодичность изменения энергии поля интервала центральной массы через скорости изменения напряженности образует систему взаимообусловленных поляризованных приливных волн, как на центральной массе, так и на массе в интервале. При этом их одноименные экстремальные значения относительно масс последовательно расположены в виде спиралей. Периодичность характеристик приливных волн соответствует закономерности Тициуса-Боде, а создающие их относительные ускорения существуют в каждой точке гравитационного поля в виде суперпозиции. Поэтому любая масса подвергается действию относительного ускорения собственного гравитационного поля сложной периодичности, которое через формообразование разрушает ее.
Поскольку относительные вертикальные ускорения в два раза превышают горизонтальные и направлены противоположно, то в переменном гравитационном поле эти направления периодически меняются. В системе координат, связанной с пробными телами в интервале, траектории движений закономерны, величины их относительных смещений линейно связаны с исходными расстояниями и обуславливают тангенциальную скорость на орбитах. Результаты предполагаемых стереотипных геометрических действий приливных волн гравитационных полей были обнаружены в формах комет и материков (океанов) Земли.
Скорости движений, формы, периоды и координаты массы или ее частей, связанные с определенными геометрическими изменениями ее собственного гравитационного поля, в своей основе являются закономерными и поэтому принципиально прогнозируемы. Учет периодичности изменения собственных гравитационных полей масс является не только теоретически, но и практически, очень важным, в частности, для оценки режимов функционирования сооружений, корректности работы измерительных приборов (особенно измеряющих вертикальные расстояния), состояния и динамики биологических систем. Такая информация необходима и для установления пространственно-временных причинно-следственных воздействий гравитации на геосферы с целью оптимизации прогнозов эволюционных и катастрофических природных изменений
Литература:
1. Бортникова Г.И. Гипотеза механизма закономерности Тициуса-Боде. Журнал Молодой ученый, № 7, 2009, с. 7-14. (http:// www.moluch.ru/ )
2. Тейлор Э., Уиллер Дж. Физика пространства-времени. М., Мир, 1971, с.229
3. Орлов С.В. Кометы. БСЭ, т.22, госиздат. БСЭ, 1953. с.134
4. Балуховский Н.Ф. Геологические циклы.Изд-во Наукова Думка, Киев, 1966,167 с.
5. Лавров А.А. Некоторые следствия движения Земли в гравитационном поле Галактики. Географический сборник, №15, Астрогеология.Изд-во АНСССР, М-Л, 1962, с.162-167.
6. Личков Б.Л. К основам современной теории Земли. Изд-во ЛГУ, 1965.
7. Грушинский Н.П., Сажина Н.Б. Гравитационная разведка. М. Недра, 1981, 391 с.
Рис.3. В крупном плане карты показаны характерные углы форм материков (океанов).
Обозначения: ___ 56о, ---- 127о , \ | / 63 о, === 27о .